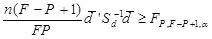
آزمون مشاهدات جفت شده
آزمون مشاهدات جفت شده
حالت یک متغیره
فرض کنید دو نمونه مستقل از یکدیگر نیستند زیرا یک جفت شدن طبیعی بین مشاهده iام yi در نمونه اول و مشاهده iام xi در نمونه دوم برای همه i ها وجود دارد.مثلا وقتی یک تیمار بر روی یک بیمار دوبار اعمال می شود. چنین جفت شدن هایی را مشاهدان جفت شده می گویند. دو نمونه حاصل که بدست می آیند دارای همبستگی می باشند. دو نمونه جفت شده را به یک نمونه به صورت جدول زیر تبدیل می کنیم:
آزمون مشاهدات جفت شده
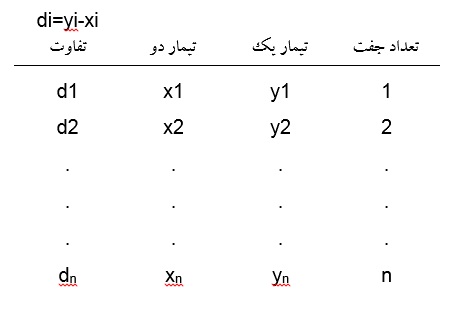
| di=yi-xi تفاوت | تیمار دو | تیمار یک | تعداد جفت |
| d1 | x1 | y1 | 1 |
| d2 | x2 | y2 | 2 |
| . | . | . | . |
| . | . | . | . |
| . | . | . | . |
| dn | xn | yn | n |
با استفاده از d1,d2 …dn خواهیم داشت:
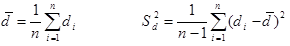
H0: µd=0, H1: µd≠0 یعنی H0: µy≠µx
اگر |t|>t α/2, n-1 باشد فرض صفر رد می شود. در اینجا لازم نیست فرض کنیم σ2x= σ2yاست زیرا محدودیتی بر روی ماتریس ∑ وجود ندارد. در اینجا لازم نیست فرض کنیم هر یک از متغیرهای x, y دارای توزیع نرمال هستند، بلکه برای تحقیق کواریانس بین x, y نیاز به فرض دیگری است و آن فرض وجود توزیع نرمال دو متغیره با میانگین و کواریانس زیر است:
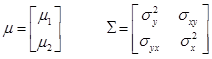
این آزمون دارای درجه آزادی (n-1) است. بطور کلی جفت شدن واریانس درون نمونه را کاهش می دهد و لذا سبب افزایش توان آزمون می شود.
حالت چند متغیره
در اینجا نیز همان جفت شدن طبیعی واحدهای طبیعی واحدهای نمونه گیری مثل حالت یک متغیره را فرض می گیریم. اما در اینجا p متغیر بر روی هر واحد نمونه گیری انجام می شود. بنابراین در اینجا داریم yi از نمونه اول با xi از نمونه دوم که در آن i=1,2…n است، جفت می شود. اگر بر روی هر واحد نمونه گیری دو تیمار اعمال شود، وضعیت به صورت زیر خواهد بود:
| di=yi-xi تفاوت | تیمار دو | تیمار یک | تعداد جفت |
| d1 | x1 | y1 | 1 |
| d2 | x2 | y2 | 2 |
| . | . | . | . |
| . | . | . | . |
| . | . | . | . |
| dn | xn | yn | n |
در t جفت شده یک متغیر فرض کردیم که y وx دارای توزیع نرمال دو متغیره هستند و بعلاوه x,y دارای همبستگی می باشند. در اینجا نیز فرض بر این است که Ӯ و Ẍ میانگین، دارای همبستگی بوده و نیز دارای توزیع نرمال چند متغیره هستند، یعنی
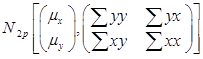
دارای
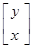
µd = E(y-x) = µy – µx , H0: µy = µx که برابر µd =0 H0: خواهیم داشت:
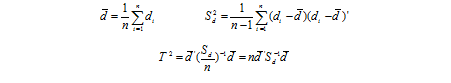
این آماره T2 دارای توزیع p, n-1 T2 می باشد. اگر T2>T2 α,p, n-1 باشد فرض صفر رد می شود. لازم به یادآوری است که Sd در فرمول بالا معادل Syy – Syx – Sxy – Sxx می باشد.
آزمون مشاهدات جفت شده
مثال:متوسط روزانه ترافیک در دو شهر A و B در زمستان و تابستان در طی 6 سال به شرح زیر است:
شهرA زمستان =y2 تابستان = y1
شهرB زمستان =x2 تابستان =x1
| شهر A | شهر B | |||
| سال | x1 | x2 | y1 | y2 |
| 1 | 2600 | 2350 | 1450 | 1300 |
| 2 | 2850 | 2350 | 1750 | 1450 |
| 3 | 2800 | 2250 | 1700 | 1350 |
| 4 | 2750 | 2200 | 1650 | 1300 |
| 5 | 2400 | 2250 | 1350 | 1250 |
| 6 | 2450 | 2300 | 1400 | 1300 |
N=6 d1 = (1150, 1050)’ … d6 = (1050, 1000)’
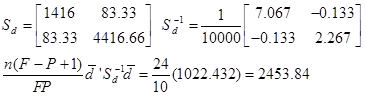
چون 2453.84 از F2,4,0.05=6.94 است، لذا فرض صفر رد می شود. در اینجا فرض صفر زمانی رد می شود که