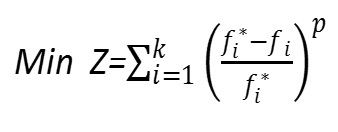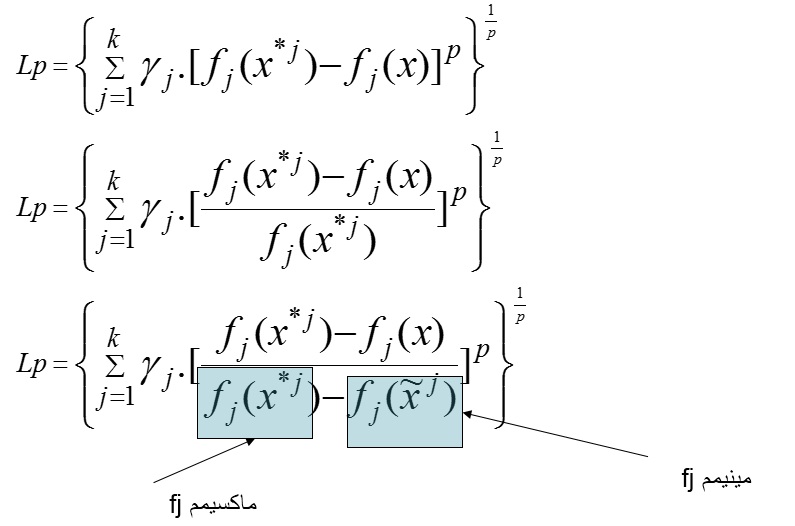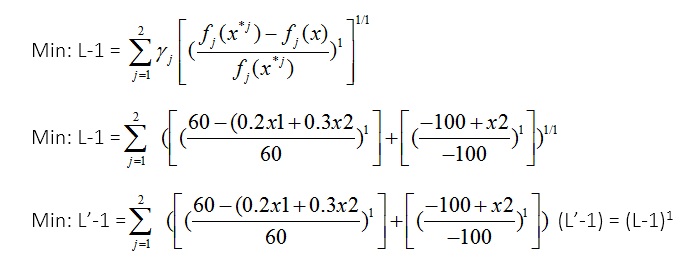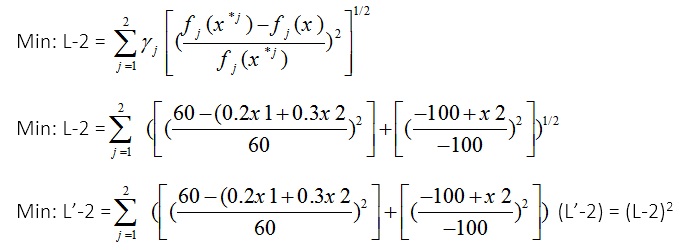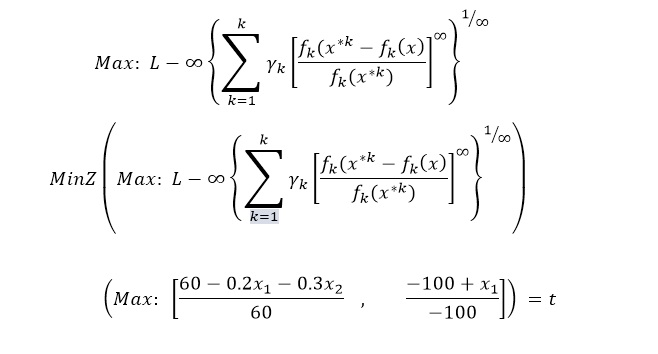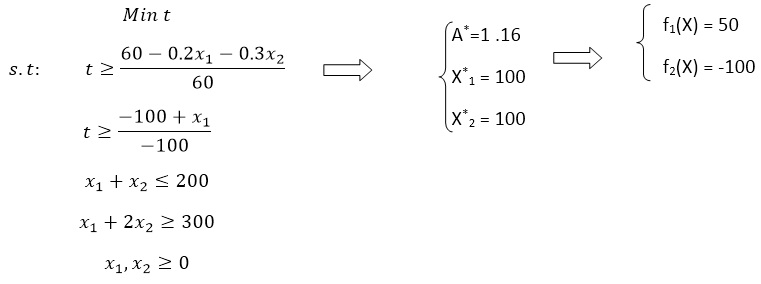
روش معیار جامع (LP متریک)

روش معیار جامع (LP متریک) یک روش تصمیم گیری چند معیاره است که برای یافتن بهترین راه حل از میان مجموعه ای از راه حل های ممکن استفاده می شود. این روش بر اساس این اصل است که هر راه حل را می توان با یک نقطه در فضای معیارها نشان داد. نقطه ای که فاصله آن از نقطه ایده آل کمترین باشد، بهترین راه حل است.

روش معیار جامع چیست

در روش معیار جامع بر خلاف روش های قبلی نیازی به اولویت بندی اهداف، وزن دهی، یا تبدیل اهداف به محدودیت نیست. روش معیار جامع، بسته به مورد، مجموع توان اول، دوم، …انحرافات نسبی اهداف از مقدار بهینه شان را حداقل می کند. در این روش، تابع هدف که همواره حداقل نمودن آن مورد توجه است به صورت زیر تعریف می شود:

که در آن  مقدار بهینه ­ی تابع هدف iام (بدون در نظر گرفتن اهداف دیگر) است. پیشنهادهای مختلفی برای مقدار P وجود دارد. برخی  را مناسب می دانند(یعنی مجموع نسبی مقدار انحرافات حداقل شود) و برخی نیز  را مناسب تر می دانند (یعنی مجموع توان دوم انحرافات حداقل شود).

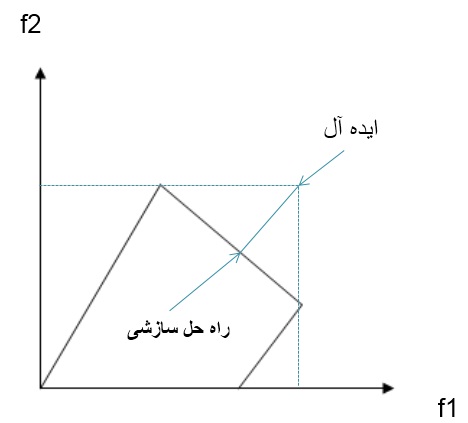
همچنین در روش معیار جامع (LP متریک) یک نقطه ایده آل در نظر گرفته می شود و سعی می شود نزدیک ترین نقطه از فضای جواب به نقطه ایده آل یافت شود. به این جواب (جواب سازشی) گفته می شود.

این نکته حائز اهمیت است که —توابع سازشی متفاوتی برای اندازه گیری فاصله استفاده می شود و این راه حل های مساله معیار جامع (LP متریک)، راه حل های موثر مساله چند هدفه هستند. معمولاً راه حل ها برای مقادیر p برابر با یک، دو و بی نهایت محاسبه می شود. به منظور محدود کردن تعداد راه حل ها، دور ترین راه حل ها از نقطه ضد ایده آل نیز محاسبه شده و راه حل های مشترک انتخاب می شوند:

مراحل روش معیار جامع

در ادامه به بررسی هر یک از این مراحل به طور مفصل می پردازیم.

تعریف معیارها

در اولین مرحله، باید معیارهای مورد استفاده در تصمیم گیری را تعریف کنیم. معیارها می توانند کمی یا کیفی باشند. معیارهای کمی معیارهایی هستند که می توان آنها را به صورت عددی اندازه گیری کرد. به عنوان مثال، هزینه، زمان، و کیفیت می توانند معیارهای کمی باشند.

معیارهای کیفی معیارهایی هستند که نمی توان آنها را به صورت عددی اندازه گیری کرد. به عنوان مثال، زیبایی، راحتی، و ایمنی می توانند معیارهای کیفی باشند.

تعیین نقطه ایده آل

در مرحله دوم، باید نقطه ایده آل را تعیین کنیم. نقطه ایده آل نقطه ای است که در آن همه معیارها به بهترین مقدار خود می رسند.

نقطه ایده آل می تواند یک نقطه واقعی یا یک نقطه فرضی باشد. به عنوان مثال، اگر هزینه و کیفیت دو معیار مورد استفاده در تصمیم گیری باشند، نقطه ایده آل نقطه ای است که در آن هزینه صفر و کیفیت بی نهایت است.

محاسبه فاصله بین راه حل ها و نقطه ایده آل

در مرحله سوم، باید فاصله بین هر راه حل و نقطه ایده آل را محاسبه کنیم. این کار معمولا با استفاده از یک تابع فاصله مانند تابع Lp انجام می شود.

تابع Lp یک تابع فاصله است که بر اساس درجه p تعریف می شود. تابع Lp به صورت زیر تعریف می شود:

Lp(x, y) = |x – y|^p

که در آن x و y دو بردار هستند و p یک عدد طبیعی است.

برای مثال، اگر p = 1، تابع Lp به عنوان تابع L1 شناخته می شود. تابع L1 فاصله بین دو بردار را با جمع کردن اختلاف بین اجزای دو بردار محاسبه می کند.

L1(x, y) = |x1 – y1| + |x2 – y2| + … + |xn – yn|

اگر p = 2، تابع Lp به عنوان تابع L2 شناخته می شود. تابع L2 فاصله بین دو بردار را با محاسبه ریشه مربعی از مجموع مربعات اختلاف بین اجزای دو بردار محاسبه می کند.

L2(x, y) = sqrt(|x1 – y1|^2 + |x2 – y2|^2 + … + |xn – yn|^2)

انتخاب راه حل با کمترین فاصله

در مرحله آخر، باید راه حلی را انتخاب کنیم که فاصله آن از نقطه ایده آل کمترین باشد. این راه حل بهترین راه حل است. به عنوان مثال، اگر دو راه حل وجود داشته باشد که فاصله آنها از نقطه ایده آل برابر باشد، راه حلی که مقدار کمتری از معیارهای کیفی را دارد، بهترین راه حل است.

الگوریتم روش معیار جامع

در روش معیار جامع، ابتدا باید نقطه ایده آل را تعریف کنیم. نقطه ایده آل نقطه ای است که در آن همه معیارها به بهترین مقدار خود می رسند. سپس، باید فاصله بین هر راه حل و نقطه ایده آل را محاسبه کنیم. این کار معمولا با استفاده از یک تابع فاصله مانند تابع Lp انجام می شود.

در نهایت، راه حلی که فاصله آن از نقطه ایده آل کمترین باشد، بهترین راه حل است.

به عنوان مثال، فرض کنید که دو معیار داریم:

• هزینه
• کیفیت

نقطه ایده آل نقطه ای است که در آن هزینه صفر و کیفیت بی نهایت است.

فرض کنید که دو راه حل داریم:

• راه حل 1: هزینه 100 و کیفیت 90
• راه حل 2: هزینه 50 و کیفیت 80

فاصله راه حل 1 از نقطه ایده آل برابر است با:

sqrt((100 – 0)^2 + (90 – inf)^2)

فاصله راه حل 2 از نقطه ایده آل برابر است با:

sqrt((50 – 0)^2 + (80 – inf)^2)

از آنجایی که فاصله راه حل 2 از نقطه ایده آل کمتر از فاصله راه حل 1 است، می توان گفت که راه حل 2 بهترین راه حل است.

روش معیار جامع یک روش ساده و موثر است که برای طیف گسترده ای از مسائل تصمیم گیری چند معیاره استفاده می شود. با این حال، ممکن است در مواردی که معیارها به شدت با هم در تضاد باشند، کارآمد نباشد.

مزایای روش معیار جامع

روش معیار جامع یک روش تصمیم گیری چند معیاره است که برای یافتن بهترین راه حل از میان مجموعه ای از راه حل های ممکن استفاده می شود. این روش بر اساس این اصل است که هر راه حل را می توان با یک نقطه در فضای معیارها نشان داد. نقطه ای که فاصله آن از نقطه ایده آل کمترین باشد، بهترین راه حل است.

در اینجا به برخی از مزایای روش معیار جامع اشاره شده است:

سادگی: روش معیار جامع یک روش نسبتا ساده است که به راحتی قابل فهم و پیاده سازی است. این روش بر اساس یک مفهوم ساده است: فاصله بین یک راه حل و نقطه ایده آل.

کارایی: روش معیار جامع معمولا کارآمد است و می تواند به سرعت بهترین راه حل را پیدا کند. این به دلیل سادگی این روش است.

انعطاف پذیری: روش معیار جامع انعطاف پذیر است و می توان آن را برای طیف گسترده ای از مسائل تصمیم گیری چند معیاره استفاده کرد. این به دلیل این است که روش معیار جامع بر اساس یک مفهوم کلی است که می تواند برای هر مجموعه ای از معیارها استفاده شود.

معایب روش معیار جامع

در ادامه به بررسی هر یک از این معایب به طور مفصل می پردازیم.

ممکن است در مواردی که معیارها به شدت با هم در تضاد باشند، کارآمد نباشد.

در مواردی که معیارها به شدت با هم در تضاد باشند، روش معیار جامع ممکن است کارآمد نباشد. به عنوان مثال، فرض کنید که دو معیار داریم:

• هزینه
• کیفیت

اگر هزینه و کیفیت با هم در تضاد باشند، ممکن است راه حلی که هزینه آن کم است، کیفیت پایینی داشته باشد. در این حالت، روش معیار جامع ممکن است راه حلی را انتخاب کند که هزینه آن کم است، اما کیفیت آن پایین است.

ممکن است به راه حلی که بهترین راه حل نیست، منجر شود.

روش معیار جامع بر اساس یک مفهوم کلی است که ممکن است منجر به انتخاب راه حلی شود که بهترین راه حل نیست. به عنوان مثال، فرض کنید که دو معیار داریم:

• هزینه
• کیفیت

اگر تصمیم گیرنده بر کیفیت بیشتر از هزینه تأکید داشته باشد، ممکن است راه حلی که هزینه آن کم است، اما کیفیت آن پایین است، بهترین راه حل نباشد. در این حالت، تصمیم گیرنده ممکن است راه حلی را ترجیح دهد که هزینه آن بیشتر است، اما کیفیت آن بالاتر است.

در مجموع، روش معیار جامع یک روش ساده و کارآمد است که می تواند برای طیف گسترده ای از مسائل تصمیم گیری چند معیاره استفاده شود. با این حال، در مواردی که معیارها به شدت با هم در تضاد باشند، ممکن است کارآمد نباشد.

مثال کاربردی روش معیار جامع (LP متریک)

مثال زیر را در نظر بگیرید و براساس روش معیار جامع (LP متریک) و به ازای P=1 و P=2 و P=INF  مساله را حل کنید:

Max f1(x) = 0.2 x1 + 0.3 x2

Min f2(x) = x2

s.to

x1 + x2 <= 200

x1 + 2×2 >= 300

x1, x2 >=0

گام اول: مشخص نمودن راه حل ایده آل برای P=1 , P=2

به منظور ارزیابی ترجیهات مدیریت شرکت دو مساله برنامه ریزی خطی زیر از طریق WINQSB حل می گردد:

مساله دوم                                                             مساله اول

Max f1(x) = 0.2 x1 + 0.3 x2                                                     Max f2(X) = -X2

s.to                                                                                          s.to

X1 + X2 <= 200                                                                        X1 + X2 <= 200

X1 + 2X2 >= 300                                                                      X1 + 2X2 >= 300

X1, X2 >=0                                                                               X1, X2 >=0

جواب های نهایی به شرح زیر است

F2	X2	F1	X1
-200	200	60	0	A
-150	150	50	100	B
-100	100	60	0	C

گام دوم: مشخص نمودن ماتریس بهره وری

	F1	F2	X1	X2
F1	60*	-200	0	200
F2	50	-100*	100	100

 گام سوم: دسترسی به یک راه حل موثر

p=1

جواب نهایی {X1*=250              X2*=0             f*1(x)= 100               f*2(x)= 250  }

p=2

Min: L’-2 = 0.0001444444X1¹+ 0.0000666667X1X2 -0.0333333333X1 + 0.0000250000X2² -0.0100000000X² + 2;

S.to

X1 + x2 <= 200

X1 + 2×2 >= 300

X1, x2 >=0

برای بدست آوردن نقطه بهینه این عبارت که از نوع QUADRATIC PROGRAMMING می باشد از نرم افزار WINQSB  استفاده می کنیم.

جواب نهایی {X1*=94.08       f*1(x)= 0.23     X2*=102.95     f*2(x) = -102.5}

گام چهارم: نمودار هندسی

ضلع BC نشان دهنده راه حل های موثر می باشد و با توجه به حل مسائل L-1 , L-2 DM  راه حلی را از بین راه حل های موجود بر می گزیند.

مشخص نمودن راه حل ایده آل برای P=INF

برای حل مسائلی از این قبیل نمی توان از راه حل معمول استفاده نمود لذا از تابع ضد ایده آل استفاده می نماییم به گونه ای که تابع را برابر عبارت t  قرار می دهیم و مینیمم ماکسیمیم عبارات را به محاسبه می نماییم.

از حل معادله بهینه فوق نقطه بهینه در بینهایت به صورت زیر خواهد بود:

سوالات متداول روش معیارجامع

تصمیم گیری چند معیاره

تصمیم‌گیری شامل بیان درست اهداف، تعیین راه‌حل‌های مختلف و ممکن، ارزیابی امکان‌پذیری آنان، ارزیابی عواقب و نتایج ناشی از اجرای هر یک از راه‌حل‌ها و بالاخره انتخاب و اجرای آن می‌باشد. کیفیت مدیریت اساساً تابع کیفیت تصمیم‌گیری است زیرا کیفیت طرح و برنامه‌ها، اثربخشی و کارآمدی راهبردها و کیفیت نتایجی که از اعمال آن‌ها بدست می‌آید همگی تابع کیفیت تصمیماتی است که مدیر اتخاذ می‌نماید.

در اکثر موارد تصمیم‌گیری‌ها وقتی مطلوب و مورد رضایت تصمیم‌گیرنده است که تصمیم‌گیری براساس چندین معیار مورد بررسی قرار گرفته باشد. معیارها ممکن است کمی یا کیفی باشند. در روش‌های تصمیم‌گیری چند معیاره که در دهه‌های اخیر مورد توجه محققین قرار گرفته‌است به جای استفاده از یک معیار سنجش بهینگی از چند معیار سنجش استفاده می‌شود.

خدمات فرابگیر

1. تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
2. مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
3. برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
4. طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
5. خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
6. پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تص
7. آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت

باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.