روش های آماری چند متغیره
روش های آماری چند متغیره آن دسته از روش های آماری هستند که به طور همزمان داده ها را بر روی چندین متغیر تجزیه می کنند. در تجزیه چند متغیره روابط همزمان متغیرها با هم مورد بحث قرار می گیرد. در این تکنیک ها پیرامون میانگین و یا واریانس یک متغیر و یا رابطه دو متغیر بحث نمی شود، بلکه کواریانس و هم بستگی های بین سه یا چند مورد بحث قرار می گیرد.
روش های آماری چند متغیره
فرض کنید یک شرکت می خواهد دو محصول مسواک و خمیر دندان را به بازار عرضه کند و مدیر کارخانه در نظر دارد که وضعیت مصرف کننده ها را از نظر این دو محصول ارزیابی کند. نوع تجزیه بستگی به این دارد که مدیر کارخانه چه چیزی را در نظر دارد. ممکن است مردم هر دو محصول را با هم مورد توجه قرار دهند. اگر دو محصول بهم وابسته باشند، در آن صورت دریافت دو محصول دارای همبستگی خواهد بود. در تجزیه رگرسیون و کورالاسیون نیز ممکن است چندین متغیر مورد بحث قرار گیرند، اما در اینجا معمولا فرض بر آن است که متغیرهای مستقل، تصادفی نبوده بلکه ثابت هستند.
در تجزبه چند متغیره داده ها را بر روی چندین متغیر مثلا مجموعه ای از X ها از قبیل X1,X2,X3,X4 و غیره به عنوان یک عنصر واحد در تجزیه مورد توجه قرار می گیرند. مثلا در تجزیه وضعیت مصرف کننده ها، مصرف کننده ها از نظر دو محصول نمره می گیرند. یعنی برای هر مصرف کننده یک جفت پاسخ وجود دارد به نام های X1,X2 لذا دو نمره دارد X1 که وضعیت مصرف کننده از نظر مسواک و دیگری X2 که وضعیت مصرف کننده از نظر خمیر دندان است. اگر k متغیر در تجزیه داشته باشیم در آن صورت K عدد بعنوان یک عنصر خواهد بود. چنین ترتیبی از داده ها را یک بردار می گویند. لذا عنصر اصلی تجزیه در اینجا بردار است.
توزیع نرمال دارای اهمیت زیادی در تجزیه های آماری است، در تجزیه چند متغیره نیز توزیع نرمال از اهمیت ویژه ای برخوردار است. توزیع نرمال در تجزیه چند متغیره عبارت از توزیع متغیر های تصادفی در یک بردار به صورت X = (X1, X2, XK) می باشد.
اگرK=2 باشد آن را حالت دو متغیره گویند و لذا با یک توزیع نرمال دو بعدی مواجه هستیم. در اینجا بجای یک منحنی زنگوله ای با یک منحنی سه یعدی پشته مانند یا تپه مانند مواجه هستیم که اگر K بزرگتر از 2 باشد آنگاه تابع احتمال دارای سطحی بیشتر از سه بعد است و نمی توان آن را رسم نمود.
اهداف کلی روش های آماری چند متغیره در پژوهش های علمی را می توان در مواردی همچون کاهش داده ها و ساده کردن ساختار، گروه بندی، رابطه بین متغیرها، پیش بینی و ساختن فرضیه و آزمون مشاهده نمود.
توزیع نرمال چند متغیره
تعمیم منحنی نرمال از یک متغیر به چندین متغیر نقش مهمی را در تجزیه چند متغیره بازی می کند. یکی از مزایای توزیع نرمال آن است که از نظر ریاضی انعطاف پذیر است و لذا می توان نتایج مفیدی را بدست آورد. اما این انعطاف پذیری فی نفسه ارزش علمی ندارد اما می توان عنوان داشت که این توزیع به دو دلیل ارزش علمی دارد. نخست اینکه در برخی از موارد دارای شرایط مدل جمعیت است و ثانیاً توزیع های نمونه گیری بسیاری از آماره های چند متغیره تقریباً و صرف نظر از جمعیت منشا دارای توزیع نرمال هستند.
اگر یک متغیر تصادفی kبعدی را با X نمایش دهیم، در آن صورت خواهیم داشت: (X=(X1, X2…XK که در آن K اعداد صحیح می باشند. برای مثال در وضعیت مصرف کننده ها نسبت به دو محصول با یک متغیر تصادفی دو بعدی یا دو جزئی مواجه هستیم لذا (X=(X1,X2 است که در آن وضعیت مصرف کننده از نظر مسواک را با X1 و از نظر خمیردندان را با X2 نشان می دهیم.
اگرX ها را با اعداد حقیقی بنویسیم در آن صورت آن هارا با x کوچک نمایش می دهیم:
(x=(x1, x2…xk
تابع توزیع احتمال تجمعی را می توان به صورت F=(X1, X2, …, XK) تعریف کرد که یک تابع احتمال توام برایK متغیر تصادفی Xi است که در آن i=1,2…k می باشد. بنابراین می توان گفت که تابع توزیع احتمال تجمعی توام یک متغیر تصادفی k بعدی عبارت است از:
= P(X1≤x1, X2≤x2…Xk ≤ xk) F=(X1, X2, …, XK)
به عنوان مثال در مثال خمیردندان و مسواک F(55, 60) احتمال توام این است که نمره وضعیت مصرف کننده برای مسواک کمتر یا مساوی 55 و وضعیت او از نظر خمیردندان کمتر یا مساوی 60 باشد.
توزیع احتمال حاشیه ای هر یک از k متغیر Xi عبارت از توزیع احتمال آن متغیر به تنهایی (صرف نظر از اینکه احتمال هر یک از اجزا متغیر تصادفی در بردار چقدر است) می باشد که در آن xi یک مقدار است.
F (Xi) = P (Xi ≤ xi)
به طور کلی تابع توزیع احتمال توام به حاصلضرب توزیع احتمال حاشیه ای گفته نمی شود زیرا مقداری همبستگی بین متغیرهای تصادفی وجود دارد یعنی مستقل از یکدیگر نیستند. اگر متغیر های تصادفی مستقل از یکدیگر باشند، دارای مزیت کمتری برای تجزیه چند متغیره است. توزیع نرمال چند متغیره یک متغیر تصادفی دارای توزیع احتمال زیر است:
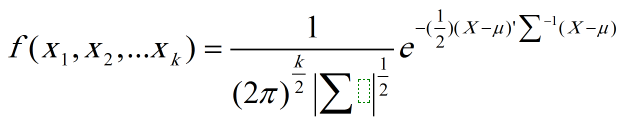
X بردار متغیر تصادفی، µ بردار میانگین های اجزا متغیرهای Xi و ∑ ماتریس واریانس کواریانس است. علامت ‘ به معنای برگردان ماتریس و -1 به معنای عکس ماتریس و || بیانگر دترمینان ماتریس می باشد.
روش-های-آماری-چند-متغیره
توزیع نرمال دو متغیره
ساده ترین توزیع نرمال چند متغیره، توزیع نرمال دو متغیره است که می توان آنرا به صورت زیر تعریف کرد. یک متغیر تصادفی نرمال دو متغیره (X=(X1,X2 دارای بردار های میانگین
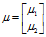
و ماتریس واریانس (∑) به صورت زیر تعریف می است.
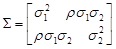
ماتریس واریانس کواریانس متقارن بوده و عناصر خارج از قطر، کواریانس X1 و X2 می باشند.
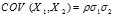
کواریانس ← P ضریب همبستگی و σ انحراف از معیار می باشد. مقادیر 21 σ 22 , σ واریانس های متغیر X1 و X2 می باشند.
حال می توان با جایگزینی مقادیر بالا توزیع نرمال چند متغیره را به صورت توزیع نرمال دو متغیره بازنویسی نمود.
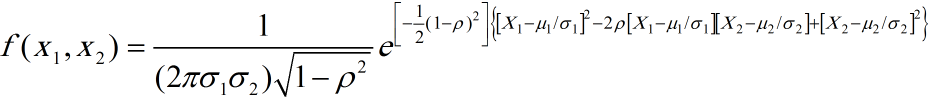
میانگین چند متغیره یک جمعیت یا توزیع را با µ1, µ2 ,…µk نمایش می دهند و آن را مرکز جمعیت یا توزیع می نامند.
ارزیابی احتمالات
در آمار تک متغیره احتمال اینکه یک متغیر تصادفی نرمال در داخل یک محدوده از یک خط قرار گیرد را بوسیله سطح زیر منحنی نرمال بین دو حد در نظر می گیرند. در یک آماره دو متغیره تصادفی احتمال اینکه بردار دو متغیره(X1, X2) در داخل ناحیه ای در فضای X1-X2 قرار گیرید را بوسیله حجم تابع نرمال دو متغیره در بالای فضای مورد نظر، مورد توجه قرار می دهند. با استفاده از توزیع کیدو می توان احتمال اینکه یک متغیر تصادفی دو متغیره در داخل یک بیضی قرار گیرد را بدست آورد.
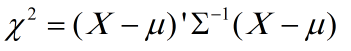
در این فرمول X, µ بردارهای چند بعدی و ∑ ماتریس واریانس-کواریانس است. مقدار نیز دارای توزیع کیدو با k درجه آزادی می باشد. بعنوان مثال، احتمال اینکه متغیر تصادفی دوتایی در داخل بیضی قرارگیرد برابراست با =5.99 با احتمال 95% که مقدار نقطه بحرانی توزیع کیدو با درجه آزادی k=2 می باشد و دارای مساحت 0.95 در طرف چپ منحنی است.
روش های آماری چند متغیره
برآورد نمونه
در آمار تک متغیره انحراف معیار جامعه برای ما معلوم نیست یعنی σ نامعلوم است و آنرا توسط انحراف معیار نمونه یعنی S برآورد می کنیم لذا توزیع احتمال نمونه بجای توزیع نرمال را بوسیله t نمایش می دهیم. به همین صورت در آمار چند متغیره نیز ماتریس واریانس-کواریانس جامعه یعنی ∑ نیز برای ما نامعلوم است و لذا باید ∑ را برآورد نموده و توزیع t معادل آن را بدست آوریم. برای برآورد∑ از ماتریس مجموع مربعات (SS) و حاصل ضرب ها (SSCP) استفاده می کنیم. ماتریس حاصل ضرب ها را به طور خلاصه با S نشان می دهیم. می توان نشان داد که S/n-1 یک ماتریس برآورد کننده نااُریب برای∑ است.
روش های آماری چند متغیره
شاخص نمونه (آماره) برای تجزیه چند متغیره
میانگین نمونه چند متغیره را مرکز نمونه گویند و عبارت از بردار میانگین نمونه های k متغیر است. خواهیم داشت:

ماتریس مجموع مربعات و مجموع حاصل ضرب ها(S) عبارت است از:
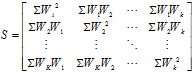
در این ماتریس Wi انحراف داده ها از نقاط Xij از میانگین Ẍi نمونه می باشد. در Wi مقدار I,j نشان دهنده تعداد نقاط در داخل اندازه نمونه(n) می باشد.
بردار همبستگی نمونه ها برای تعداد n اندازه گیری و بر روی P متغیر به صورت زیر نمایش داده می شود:
روش-های-آماری-چند-متغیره
مثال: تعداد کتاب های فروخته شده در 4 مرحله و مقدار فروش به شرح زیر است.
متغیر یک ( مقدار فروش): 42 52 48 58
متغیر دوم ( تعداد کتاب): 4 5 4 3
ابتدا اعداد را در قالب ماتریس می نویسیم:

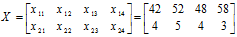
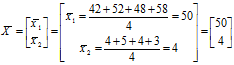
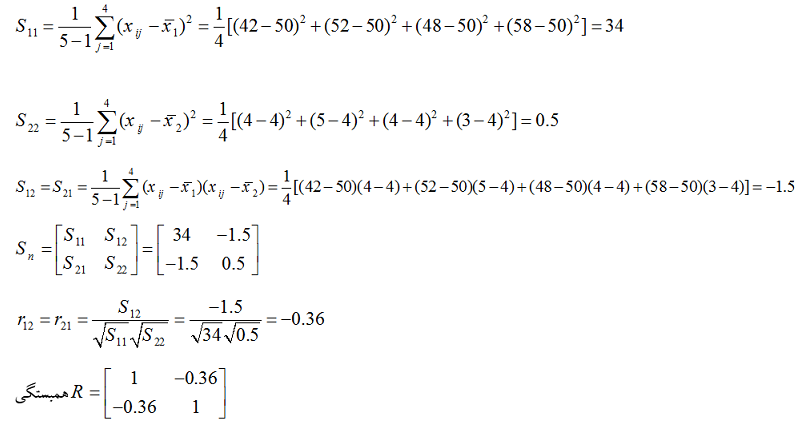
مطلب بسیار خوبی بود.ممنون
ممنونم از شما
سلام.ممنون .خیلی خوب بود.از دست اندرکاران وبسایت به این خوبی
سپاسگزارم
ممنونم از شما
سلام.واقعا وبسایت خوبی دارید
خسته نباشید مرسی به خاطر این مطلب مفید
وای خیلی خوبه ساییتون
ممنون و متشکر
تو زمینه ای که فعالیت میکنید جزو بهترین سایت ها هستید.
ممنونیم
سلام.خواستم بابت وبسایت خوبتون
ازتون تشکر کنم و امیدوارم باعث ایجاد انگیزه براتون بشه
خیلی ممنونیم.
سلام لطفا در مورد کواریانس چند متغیره وپیش فرضهای ان مطلب بگذارید ممنون
با سلام حتما در اولین فرصت