محتوای اختصاصی
مطالب انحصاری تیم فرابگیر
ثبت سفارشات
در کوتاه ترین زمان و قیمت مناسب

پشتیبانی آنلاین
پاسخگویی سریع و مطمئن
آخرین مطالب آموزشی
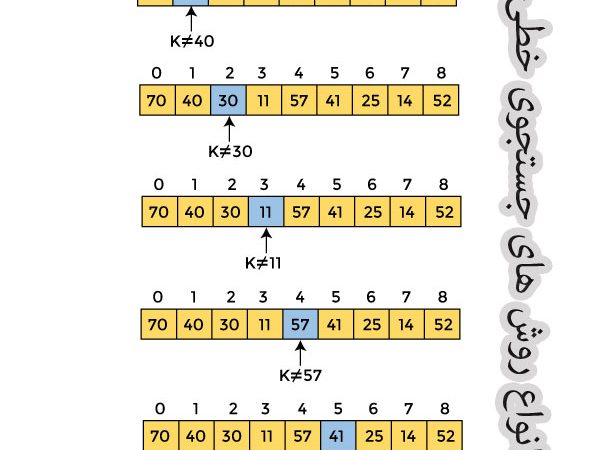
روش های جستجوی خطی، الگوریتم هایی ساده و کارآمد برای یافتن یک عنصر خاص در یک لیست یا آرایه هستند. این روش ها به طور خطی با اندازه لیست یا
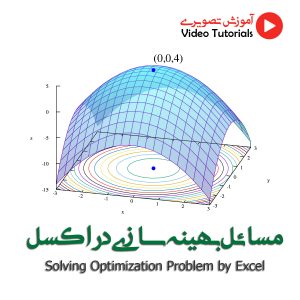
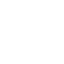
در بسیاری از مسائل علمی و مهندسی، یافتن نقطه بهینه یک تابع، چالشی مهم محسوب می شود. این نقطه، بهترین مقدار تابع را در فضای جستجو نشان می دهد. روش
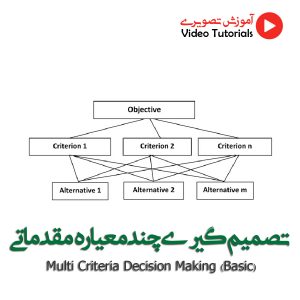
انتخاب بهترین گزینه از بین چندین گزینه با معیارهای مختلف، چالشی است که در بسیاری از زمینه ها با آن روبرو هستیم. روش UTA (Utility Theory Additive) روش مطلوبیت جمع