مثال روش الکتره فازی
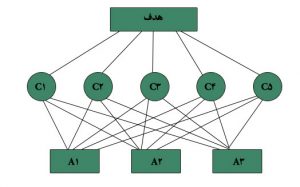
یک شرکت قصد دارد، از بین 5 تامین کننده بر اساس معیارهای C1 تا C5 که به ترتیب سودآوری تامین کننده، میزان سهولت ارتباط با تامین کننده، ظرفیت های تکنولوژیکی، مطابقت سطح کیفی با سطح شرکت و قدرت تشخیص خطا می باشند، مطلوب ترین تامین کننده را انتخاب کند. بر اساس جدول اطلاعات زیر، مساله را از طریق روش الکتره فازی حل نموده و گزینه ارجح را اعلام نمایید.
مثال روش الکتره فازی
گام اول: ماتریس تصمیم نرمالایز شده به صورت زیر درنظر گرفته شده است.
| A1 | 0.583 | 0.725 | 0.768 | 0.873 | 0.594 | 0.708 | 0.738 | 0.841 | 0.575 | 0.752 | 0.786 | 0.916 | 0.596 | 0.701 | 0.732 | 0.837 |
| A2 | 0.197 | 0.476 | 0.514 | 0.799 | 0.615 | 0.757 | 0.799 | 0.905 | 0.73 | 0.852 | 0.934 | 0.979 | 0.502 | 0.652 | 0.681 | 0.783 |
| A3 | 0.682 | 0.814 | 0.854 | 0.936 | 0.626 | 0.761 | 0.78 | 0.888 | 0.498 | 0.636 | 0.684 | 0.829 | 0.474 | 0.581 | 0.645 | 0.758 |
| وزن | 0.218 | 0.218 | 0.218 | 0.218 | 0.041 | 0.041 | 0.041 | 0.041 | 0.183 | 0.183 | 0.183 | 0.183 | 0.558 | 0.558 | 0.558 | 0.558 |
گام دوم شاخص ها را در اوزان تعیین شده ضرب می نماییم تا ماتریس نرمال وزین بدست آید.
| A1 | 0.127 | 0.158 | 0.167 | 0.190 | 0.024 | 0.029 | 0.030 | 0.034 | 0.105 | 0.138 | 0.144 | 0.168 | 0.333 | 0.391 | 0.408 | 0.467 |
| A2 | 0.043 | 0.104 | 0.112 | 0.174 | 0.025 | 0.031 | 0.033 | 0.037 | 0.134 | 0.156 | 0.171 | 0.179 | 0.280 | 0.364 | 0.380 | 0.437 |
| A3 | 0.149 | 0.177 | 0.186 | 0.204 | 0.026 | 0.031 | 0.032 | 0.036 | 0.091 | 0.116 | 0.125 | 0.152 | 0.264 | 0.324 | 0.360 | 0.423 |
گام سوم دیفازی کردن مقادیر
در این قسمت جهت سهولت کار متغیرها را از فازی به قطعی تبدیل می کنیم و به این عمل دیفازی سازی می گویند.
به طور مثال برای شاخص اول میانگین 0.161 = 4/(0.127+0.158+0.167+0.190)
| A1 | 0.161 | 0.030 | 0.139 | 0.400 |
| A2 | 0.108 | 0.032 | 0.160 | 0.365 |
| A3 | 0.179 | 0.031 | 0.121 | 0.343 |
گام چهارم تشکیل ماتریس هماهنگی C
| A12 | 0.218 | 0.041 | – | – | 0.259 |
| A13 | – | 0.041 | 0.183 | – | 0.224 |
| A21 | – | – | 0.183 | 0.558 | 0.741 |
| A23 | – | – | 0.183 | – | 0.183 |
| A31 | 0.218 | – | – | 0.558 | 0.776 |
| A32 | 0.218 | 0.041 | – | 0.558 | 0.817 |
مثال روش الکتره فازی مثال روش الکتره فازی مثال روش الکتره فازی مثال روش الکتره فازی
در ادامه مجموع هر ستون در ماتریس مورد نظر قرار می گیرد. به طور مثال 0.259 در سطر اول و ستون دوم قرار می گیرد.
| A1 | A2 | A3 | |
| A1 | – | 0.259 | 0.224 |
| A2 | 0.741 | – | 0.183 |
| A3 | 0.776 | 0.817 | – |
سپس میانگین عناصر ماتریس محاسبه می شود 0.50=6/(0.259+0.224+…) . هر عنصری که مقدار آن از 0.5 کمتر باشد مقدار 0 و هر کدام که بیشتر باشد مقدار 1 را به خود اختصاص می دهد تا ماتریس هماهنگی موثر F تشکیل شود.
| A1 | A2 | A3 | |
| A1 | – | 0 | 0 |
| A2 | 1 | – | 0 |
| A3 | 1 | 1 | – |
گام پنجم تشکیل ماتریس ناهماهنگی D
- در این گام ابتدا قدرمطلق اختلاف میان در دو گزینه مورد نظر را محاسبه می کنیم. به طور مثال 0.0525 =|A12C1=|0.161-0.108
- سپس ماکزیمم شاخص هایی را در که ماتریس هماهنگی قرار نمی گیرند را محاسبه می نماییم و در ستون MAX loss قرار می دهیم. برای مثال MAX(0.0213,0.0346)= 0.0346
- در ادامه ماکزیمم هر ردیف را محاسبه کرده و در ستون Max row قرار می دهیم.
- در آخر جهت محاسبه مقدار ناهماهنگی مقدار Max loss را بر Max row تقسیم می نماییم تا مقدار ناهماهنگی در شاخص محاسبه گردد.
| C1 | C2 | C3 | C4 | Max Loss | Max row | loss/row | |
| A12 | 0.0525 | 0.0020 | 0.0213 | 0.0346 | 0.0346 | 0.0525 | 0.6592 |
| A13 | 0.0184 | 0.0018 | 0.0175 | 0.0569 | 0.0569 | 0.0569 | 1.0000 |
| A21 | 0.0525 | 0.0020 | 0.0213 | 0.0346 | 0.0525 | 0.0525 | 1.0000 |
| A23 | 0.0709 | 0.0002 | 0.0388 | 0.0223 | 0.0709 | 0.0709 | 1.0000 |
| A31 | 0.0184 | 0.0018 | 0.0175 | 0.0569 | 0.0175 | 0.0569 | 0.3071 |
| A32 | 0.0709 | 0.0002 | 0.0388 | 0.0223 | 0.0388 | 0.0709 | 0.5476 |
در ادامه مجموع هر ستون در ماتریس مورد نظر قرار می گیرد. به طور مثال 0.6592 در سطر اول و ستون دوم قرار می گیرد.
| A1 | A2 | A3 | |
| A1 | – | 0.659 | 1.000 |
| A2 | 1.000 | – | 1.000 |
| A3 | 0.307 | 0.548 | – |
مثال روش الکتره فازی مثال روش الکتره فازی مثال روش الکتره فازی مثال روش الکتره فازی
سپس میانگین عناصر ماتریس محاسبه می شود 0.75=6/(0.659+1.000+…) . هر عنصری که مقدار آن از 0.75 کمتر باشد مقدار 1 و هر کدام که بیشتر باشد مقدار 0 را به خود اختصاص می دهد تا ماتریس هماهنگی موثر F تشکیل شود.
| A1 | A2 | A3 | |
| A1 | – | 1 | 0 |
| A2 | 0 | – | 0 |
| A3 | 1 | 1 | – |
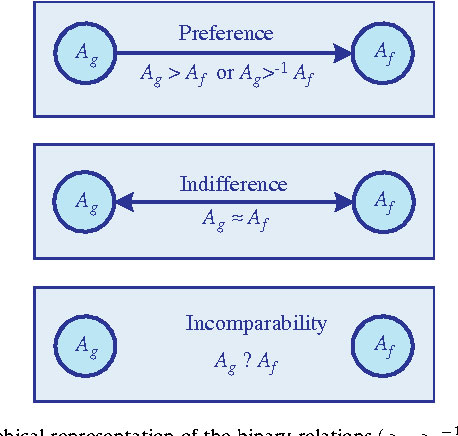
در این گام برای تعیین برتری ها دو ماتریس F و G در هم ضرب برداری می شوند.
این ضرب به گونه ای است که وقتی هر دو مقدار ۱ باشد جواب یک می گردد و در غیر این صورت جواب ۰ خواهد بود.
| A1 | A2 | A3 | |
| A1 | – | 0 | 0 |
| A2 | 0 | – | 0 |
| A3 | 1 | 1 | – |
در این مرحله تعداد ۱ و ۰ های هر ردیف شمرده می شود. مانند جدول زیر جمع یک ها در ستون Win و جمع صفرها در ستون loss و اختلاف آن ها در Different قرار می گیرد. سپس بر اساس ستون Different شاخص ها رتبه بندی می شوند.
| Win | Loss | Different | Rank | |
| 0 | 2 | -2 | 2 | A1 |
| 0 | 2 | -2 | 2 | A2 |
| 2 | 0 | 2 | 1 | A3 |
همان طور که مشاهده می شود شاخص A3 دارای رتبه اول می باشند و دو شاخص A1 ,A2 داریی یک رتبه برتری می باشند که نمی توان در مورد برتری آنها از یکدیگر نظری داشت.