مثال روش دیمتل DEMATEL
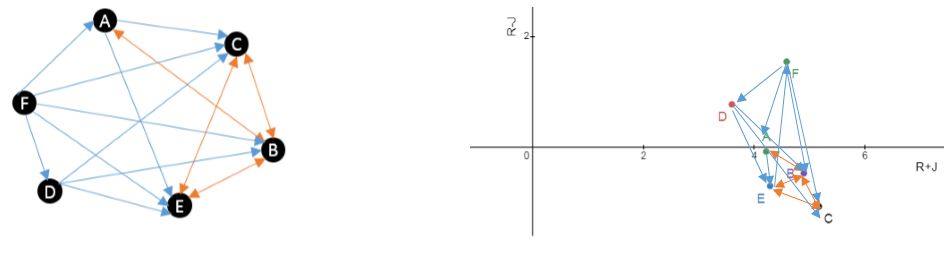
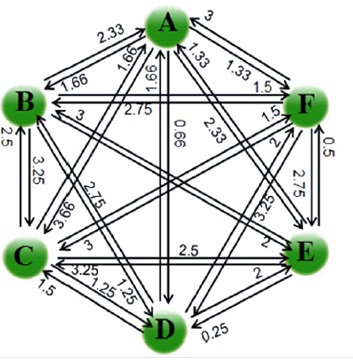
مثال روش دیمتل DEMATEL، فرض کنید دیاگراف روابط مستقیم 6 عامل A, B, C, D, E, F به صورت زیر می باشد. روش دیمتل را گام به گام بر روی آن اعمال کرده و سلسله مراتب آنها را مشخص نمایید.
گام اول: تشکیل ماتریس Mمثال روش دیمتل DEMATEL
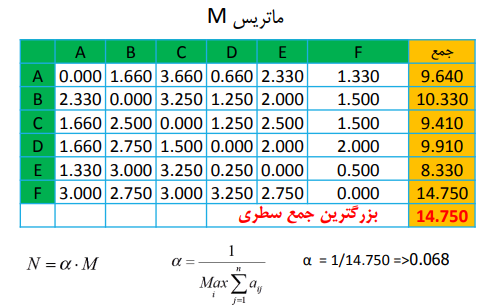
براساس روابط مشخص شده بر روی گراف، ماتریس M را تشکیل می دهیم. به طور مثال ارتباط میان A-F برابر 1.33 خواهد بود. سپس مجموع هر کدام از سطرهای ماتریس را محاسبه می نماییم و بزرگترین مقدار جمع سطری را بدست می آوریم.
مثال روش دیمتل DEMATEL
گام دوم: محاسبه مقدار α
با توجه به فرمول مدنظر که همان معکوس بزرگترین مقدار جمع سطری است مقدار α بدست می آید.
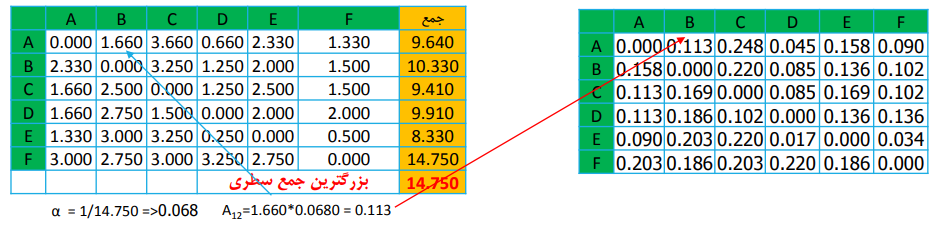
مقدار بدست آمده را در تمامی عناصر ماتریس ضرب می نماییم تا ماتریس N بدست آید
(به این عمل نرمال سازی ماتریس M گفته می شود)
α= (1/14.75) =0.068
به طور مثال برای عنصر A -D = 0.660 * 0.068 = 0.045

مثال روش دیمتل DEMATEL
گام سوم : محاسبه ماتریس معکوسه I-N)-1)
گام چهارم : محاسبه ماتریس روابط کل S = N(I-N)-1
با ضرب ماتریس N در معکوس خود ماتریس S بدست می آید. در ادامه مجموع سطری ماتریس S برابر R و مجموع ستونی ماتریس S مقدار J را تشکلیل می دهد.
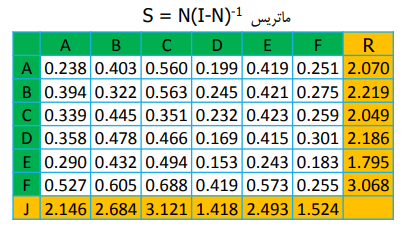
گام پنجم : تعیین میزان تاثیرگذاری و تاثیر پذیری عوامل
با رتبه بندی این مقادیر تاثیر گذاری و تاثیر پذیری آن ها محاسبه شده و برای رسم آن بر روی گراف نیز مقدار R+J و R-J محاسبه می شود.
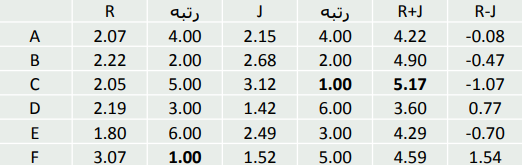
مثال روش دیمتل DEMATEL
گام ششم : رسم ﻧﻘﺸﻪ رواﺑﻂ ﺷﺒﮑﻪ ( NRM )
محور مختصات را با X= R+J و Y = R -J ترسیم نموده و مقادیر بدست آمده برای هر کدام از عوامل را بر روی آن مشخص می نماییم. سپس از ماتریس S میانگین می گیریم. سپس مقادیری را که از میانگین کمتر می باشند صفر و مابقی اعداد را در نظر می گیریم.
ماتریس بدست آمده شدت روابط هر کدام از عناصر بر یکدیگر را به ما نشان می دهد.
در صورتی که در ماتریس بدست آمده برروی قطر اصلی اعداد وجود داشته باشد بدین معناست که عنصر دارای حلقه بوده و با خود رابطه دارد.
میانگین ماتریس S برابر 0.372 می باشد.
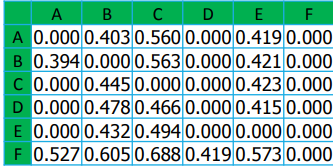
ماتریس S همان ماتریس عنوان شده در بالاست
تمامی عواملی که از 0.372 کمتر می باشند برابر 0 و سایر مقادیر برای ترسیم نوشته می شوند.