تصمیم گیری چند شاخصه فازی
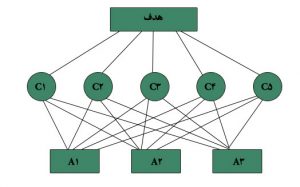
در تصمیم گیری چند شاخصه، هدف انتخاب گزینه برتر بین چندین گزینه با در نظر گرفتن معیارهای مورد نظر است. در حالت عمومی m گزینه وجود دارد که می بایست با در نظر گرفتن n معیار بررسی شود. در ساده ترین حالت فرض بر این است که معیارها از درجه اهمیت یکسانی برخوردار هستند.
تصمیم گیری چند شاخصه فازی تصمیم گیری چند شاخصه فازی
تصمیم گیری چند شاخصه فازی
مثال: مسئه طراحی دامنه الکترونیکی اتوبوس را در نظر بگیرید. در این مساله سعی می کنیم پروتکل ارتباطی مناسبی را بین سه گزینه انتخاب کنیم. سه گزینه عبارتند از:
- CSMA/CD
- MAADS
- TP

فرض کنید این گزینه ها در یک سیستم با معیارهای عملکردی سلسله مراتبی با در نظرگرفتن فاکتورهایی مانند موارد زیر ارزیابی میشوند:
- یکپارچگی سیستم
- پاسخ
- ساختار پیام
- استراتژی کنترل شبکه منعطف
- هزینه و پیچیدگی
- سازگاری
- دامنه خطا
- ردیابی خطا (FD)
- شمولیت خطا (FC)
- تجزیه خطا(FI)
- اصلاح سیستم(RC)
با توجه به فاکتورهای مطرح شده چهار هدف به شرح زیر تعریف می شود:
- پروتکل می باسیت توانایی تعیین ردیابی عملیات اشتباه را داشته باشد. (FD)
- پروتکل می بایست توانایی اندازه گیری وسعت و اندازه خطاهای ممنوع در سیستم را که از کل سیستم نشأت می گیرد داشته باشد (FC)
- پروتکل می بایست توانایی تجزیه خطا را داشته باشد (FI)
- پروتکل می بایست مهیا اصلاح سیستم باشد (RC)
گزینه های تصمیم گیری X={CSMA/CD , MAADS, TP}
اهداف تصمیم گیری G1=FD G2=FC G3=FI G4=RC
در این مساله محدودیتی وجود ندارد و اهداف توسط خبرگان اندازه گیری شده و نتایج ذیل بدست آمده است.
G1= {0.5, 0.7, 0.3}
G2= {0.5, 0.4, 0.8}
G3= {0.2, 0.01, 0.6}
G4= {0.6, 0.4, 0.9}
تصمیم گیری چند شاخصه فازی تصمیم گیری چند شاخصه فازی
با درنظر گرفتن روش تعیین تصمیم متناسب، تابع عضویت با اشتراک اهداف به دست می آید.
D(x) = G1 П G2 П G3П G4
µD(x) = minx {Gi(x)}={minx1 (0.5,0.5,0.2,0.7),minx2(0.7,0.4,0.01,0.4),minx3(0.3,0.8,0.6,0.9)
µD(x) = {0.2 , 0.01, 0.3}
تصمیم بهینه معادل حداکثر درجه عضویت در تابع عضویت تصمیم است که به صورت ذیل بدست می آید:
X*=arg{max(x)D(x)} -> arg{max(0.2 , 0.01 , 0.3 )} =arg {0,3} x*=x3
پس پروتکل سوم بهینه است
نکته: حال اگر عناصر نسبت به هم ارجحیت داشته باشند ماتریس n*n را به نام ماتریس ارزش مقایسه زوجی معیارها تشکیل می دهند. پس از تکمیل ماتریس با جمع عناصر هر سطر و تقسیم آن بر جمع کل عناصر ماتریس وزن معیار مربوط به سطر بدست می آید.
تصمیم گیری چند شاخصه فازی تصمیم گیری چند شاخصه فازی
مثال تصمیم گیری چند شاخصه فازی با وزن
مثال قبل را با ماتریس مقایسه نسبی معیارها به صورت ذیل حل می کنیم:
| ماتریس مقایسات زوجی | ||||||
| FD | FC | FI | RC | جمع | وزن | |
| FD | 1 | 5 | 3 | 1 | 10 | 0.311 |
| FC | 0.2 | 1 | 0.14 | 0.14 | 1.48 | 0.046 |
| FI | 0.33 | 7 | 1 | 0.33 | 8.66 | 0.269 |
| RC | 1 | 7 | 3 | 1 | 12 | 0.373 |
| جمع | 2.53 | 20 | 7.14 | 2.47 | 32.14 | 1.000 |
D (CSMA/CD) = {min (0.5 0.31 , 0.5 0.05 , 0,2 0.27 , 0.6 0.37)} =min(0.80, 0.96, 0.65, 0.83) = 0.65
D (MAADS) =0.29
D (TP) =0.69 بهینه
X* = TP = arg {max D(x)}
همانطور که پیشتر ذکر شد، مدل های MADM برای انتخاب مناسب ترین گزینه از بین گزینه های ممکن بکار می روند. این مدل ها معمولا توسط یک ماتریس تصمیم به صورت زیرفرموله می شوند:
تصمیم گیری چند شاخصه فازی تصمیم گیری چند شاخصه فازی
در این ماتریس، Ai بیانگر گزینه iام، xj نشانگرشاخص jام، aij نشان دهنده ارزش شاخص jام برای گزینه iام است. روش های MADM معمولا شامل دو مرحله به صورت زیر می باشند:
- اجماع نقطه نظرات نسبت به شاخص ها و گزینه ها
- ترتیب گزینه ها بر اساس نقطه نظرات جمعه
در مدل های MADM قطعی معمولا فرض بر این است که نقطه نظر نهایی در مورد یک گزینه به صورت یک عدد حقیقی بیان می گردد، اما در شرایط واقعی ممکن است دیگر این فرض وجود نداشته باشد و نتوان از اعداد طبیعی برای بیان اهمیت شاخص ها یا ارزش گزینه ها نسبت به شاخص ها مختلف استفاده کرد، در این حالت روش های FMADM مناسب می باشند.
درادامه دو مدل از مدل های FMADM تشریح می گردد. ابتدا مدل یاگر که به روشنی ساختار اینگونه مسائل را توضیح می دهد بیان می گردد و در ادامه آن مدل فرایند تحلیل سلسله مراتبی فازی(FAHP) گسترش یافته توسط یانگ بیان می گردد.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چند معیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.