روش نیوتن-رافسون (Newton-Raphson Method) یک الگوریتم عددی قدرتمند برای یافتن ریشه معادلات غیرخطی تک متغیره است. این روش از تقریب خطی برای تخمین ریشه معادله در هر مرحله استفاده میکند.
ریشه این روش به قرن هفدهم و دو ریاضیدان برجسته، اسحاق نیوتن و جوزف رافسون، باز میگردد. نیوتن ایده اصلی این روش را در سال 1685 ارائه کرد و رافسون در سال 1690 آن را به طور کامل شرح داد.
آنچه می خوانید
کاربرد روش نیوتن-رافسون
روش نیوتن-رافسون (Newton-Raphson Method) یک الگوریتم عددی قدرتمند برای یافتن ریشه معادلات غیرخطی تک متغیره است. این روش کاربردهای گستردهای در زمینههای مختلف دارد، از جمله:
مهندسی:
- تحلیل سازه ها: برای محاسبه تنش، کرنش و تغییر شکل سازه ها
- طراحی سیستم ها: برای یافتن پارامترهای بهینه سیستم ها
- کنترل فرآیندها: برای کنترل دما، فشار و سایر متغیرهای فرآیند
علوم کامپیوتر:
- هوش مصنوعی: برای آموزش شبکه های عصبی مصنوعی
- یادگیری ماشین: برای حل مسائل رگرسیون و طبقه بندی
- پردازش تصویر: برای تشخیص اشیاء و چهره ها
مسائل مالی:
- تحلیل سهام: برای پیش بینی قیمت سهام
- مدیریت ریسک: برای محاسبه ارزش در معرض خطر (VaR)
- قیمت گذاری اوراق قرضه: برای محاسبه قیمت اوراق قرضه
علوم پایه:
- فیزیک: برای حل معادلات دیفرانسیل
- شیمی: برای شبیه سازی واکنش های شیمیایی
- زیست شناسی: برای مدل سازی سیستم های بیولوژیکی
- ریاضیات: برای یافتن ریشه معادلات چند متغیره
پزشکی:
- تصویربرداری پزشکی: برای بازسازی تصاویر پزشکی
- تشخیص بیماری: برای تجزیه و تحلیل داده های پزشکی
- درمان بیماری: برای برنامه ریزی درمان های پزشکی
مزایای روش نیوتن-رافسون
- سرعت: این روش در مقایسه با روشهای دیگر مانند روش نصف کردن بازه، سرعت همگرایی بالاتری دارد.
- دقت: به طور کلی، روش نیوتن-رافسون به دقت بالایی در یافتن ریشهها دست مییابد.
- سادگی: پیادهسازی این روش نسبتاً ساده است.
- کاربرد گسترده: این روش در حل مسائل مختلف مهندسی، فیزیک و ریاضیات کاربرد دارد.
معایب روش نیوتن-رافسون
- همگرایی: این روش همیشه همگرا نمیشود. در برخی موارد، ممکن است به ریشه مورد نظر نرسد یا به سمت بینهایت میل کند.
- انتخاب نقطه شروع: دقت و سرعت روش نیوتن-رافسون به انتخاب نقطه شروع مناسب بستگی دارد.
- مشتقپذیری: تابع مورد نظر باید مشتقپذیر باشد.
- خطای گردشی: محاسبه مشتق تابع میتواند خطای گردشی را به همراه داشته باشد.
گامهای روش نیوتن-رافسون:
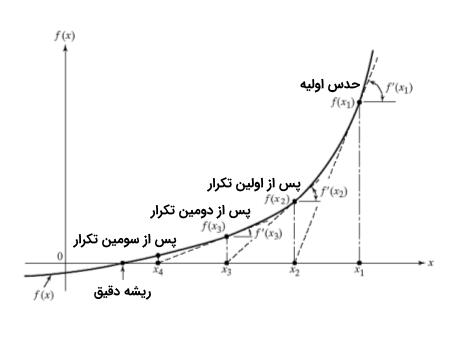
انتخاب نقطه شروع
مجدداً فرض نمایید ما با مشکل به حداقل رساندن تابع f با یک متغیر واقعی X مواجه باشیم. حال فرض می کنیم که در هر نقطه اندازه گیری (X(k می توانیم، مشتق اول ((f'(X(k ، مشتق دوم ((f”(X(k تابع ((f (X(k را محاسبه نماییم.
محاسبه مشتق
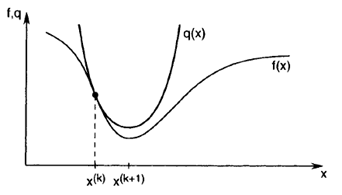
با این فرض می توانیم یک تابع درجه دوم را از طریق منطبق نمودن تابع ((f (X(k با مشتق اول و دوم آن با تابعf بدست آورد. این تابع درجه دوم به صورت زیر می باشد:
q(x) = f(X(k)) + f'(X(k)) (x – x(k)) + 1/2 f”(X(k)) (x – x(k))2
توجه داشته باشید که ((f (X(k)) = q (X(k))، f’ (X(k)) = q’ (X(k))، f” (X(k)) = q”(X(k خواهد بود. سپس، به جای به حداقل رساندن تابع f ، ما تقریب آنq را به حداقل می رسانیم.. شرط لازم مرتبه اول برای حداقل رساندن q برابر خواهد بود با:
0 = q'(x) = f'(x(k))+ f”(x(k)) (x – x(k))2
محاسبه نقطه بعدی
با جایگزینی مقدار (x = x (k+1 خواهیم داشت:
x (k+1) = x (k) – (f'(x(k)) / f”(x(k)))
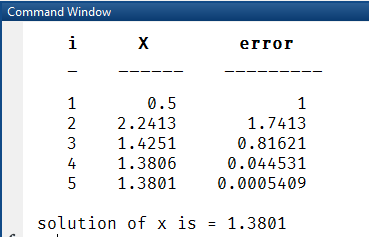
تکرار
گامهای 2 و 3 را تا زمانی که به دقت مورد نظر برسید، تکرار کنید.
نکات:
- اگر مشتق تابع در نقطه x0 صفر باشد، روش نیوتن-رافسون در آن نقطه همگرا نمیشود.
- اگر تابع در نقطه x0 دارای نقطه خم باشد، روش نیوتن-رافسون ممکن است به سمت ریشه مورد نظر همگرا نشود.
- برای افزایش دقت روش نیوتن-رافسون، میتوان از روشهای مختلفی مانند روش برنت استفاده کرد.
نتیجهگیری
روش نیوتن-رافسون یک روش قدرتمند برای یافتن ریشههای توابع پیوسته و مشتقپذیر است. این روش مزایای متعددی مانند سرعت بالا، دقت و سادگی دارد. با این حال، این روش معایبی مانند عدم همگرایی در برخی موارد و وابستگی به انتخاب نقطه شروع مناسب نیز دارد.
در انتخاب روش مناسب برای یافتن ریشههای یک تابع، باید به مزایا و معایب هر روش توجه کرد. روش نیوتن-رافسون در بسیاری از موارد، انتخابی مناسب است، اما در برخی موارد خاص، ممکن است روشهای دیگر مانند روش نصف کردن بازه یا روش برنت، کارایی بیشتری داشته باشند.
از مشاوره با ما پشیمان نمی شوید
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.
