مثال روش نیوتن رافسون

قبل از حل مثال روش نیوتن رافسون باید بدانیم که روش نیوتن-رافسون یک روش قدرتمند برای یافتن ریشه‌های توابع پیوسته و مشتق‌پذیر است. این روش مزایای متعددی مانند سرعت بالا، دقت و سادگی دارد. با این حال، این روش معایبی مانند عدم همگرایی در برخی موارد و وابستگی به انتخاب نقطه شروع مناسب نیز دارد.

در انتخاب روش مناسب برای یافتن ریشه‌های یک تابع، باید به مزایا و معایب هر روش توجه کرد. روش نیوتن-رافسون در بسیاری از موارد، انتخابی مناسب است، اما در برخی موارد خاص، ممکن است روش‌های دیگر مانند روش نصف کردن بازه یا روش برنت، کارایی بیشتری داشته باشند.

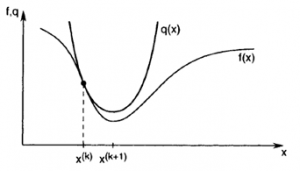
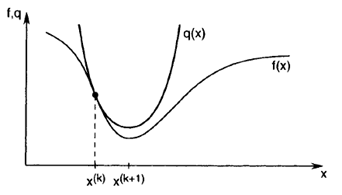
با توجه به شکل زیر مشاهده می شود که تا زمانی که مقدار مشتق دوم بیشتر از صفر باشد روش نیوتن روش مناسبی برای حل مسائل حداقل رسانی خواهد بود.

مثال روش نیوتن رافسون

با استفاده از روش نیوتن رافسون مقدار حداقل x را در تابع F(x) = 1/2 x² – sin x بدست آورید. مقدار اولیه x⁽⁰⁾ = 0.5 می باشد. حدقل دقت مورد نیاز e = 10^-5 به شرطی که x ^(k+1) – x^(k)| < e| باشد.

1)انتخاب نقطه شروع

نقطه x0​=0.5 را به عنوان نقطه شروع انتخاب می‌کنیم.

F'(x) = x – cos x           F”(x) = 1 + sin x

X⁽¹⁾ = 0.5 – (0.5 –cos 0.5 / 1 + sin 0.5 ) = 0.7552

2)محاسبه مشتق

مشتق تابع را محاسبه می کنیم.

X⁽²⁾ = X⁽¹⁾ – (f'(x⁽¹⁾) / f”(x⁽¹⁾)) = x⁽¹⁾ – (0.02710 / 1.685) = 0.7391

3)محاسبه نقطه بعدی و تکرار

حال همین روند را برای سایر مقادیر به کار می بریم لذا خواهیم داشت:

X⁽³⁾ = X⁽²⁾ – (f'(x⁽²⁾) / f”(x⁽²⁾)) = x⁽²⁾ – (9.461* 10^-5 / 1.673) = 0.7390

X⁽⁴⁾ = X⁽³⁾ – (f'(x⁽³⁾) / f”(x⁽³⁾)) = x⁽³⁾ – (1.17 * 10^-9 / 1.673) = 0.7390

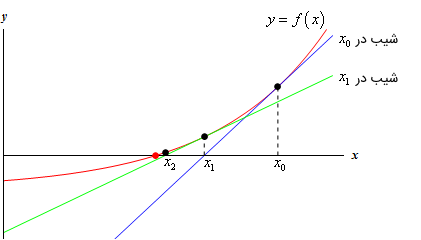
مشاهده می شود x ⁽⁴⁾ – x⁽³⁾| < 10^-5| می باشد. همچنین مقدار  f'(x⁽⁴⁾) = -8.6 * 10 ^-6 = 0 می باشد. از طرفی f”(x⁽⁴⁾) = 1.673 >0 می باشد. با این تفاسیر مقدار ⁽x⁽⁴  را می توانیم یک نقطه مینیم مطلق نامیم.

مثال روش نیوتن رافسون مثال روش نیوتن رافسون مثال روش نیوتن رافسون مثال روش نیوتن رافسون

سوالات متداول

از مشاوره با ما پشیمان نمی شوید

خدمات فرابگیر

1. تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
2. مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
3. برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
4. طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
5. خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
6. پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
7. آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت

باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.