وزن دهی در AHP
روش AHP (Analytic Hierarchy Process) یکی از پرکاربردترین روشهای تصمیمگیری چندمعیاره است که برای وزن دهی معیارها در مسائل پیچیده استفاده میشود. در بسیاری از مسائل واقعی، تصمیمگیرنده با مجموعهای از معیارهای مختلف روبهروست که اهمیت یکسانی ندارند و لازم است میزان تأثیر هر معیار بهصورت عددی مشخص شود. وزن دهی در AHP دقیقاً برای پاسخ به همین نیاز طراحی شده است.
در این روش، بهجای وزن دهی مستقیم و ذهنی، معیارها بهصورت مقایسههای زوجی با یکدیگر مقایسه میشوند. این کار باعث میشود تصمیمگیرنده بتواند اهمیت نسبی معیارها را با دقت و سازگاری بیشتری بیان کند. نتیجه این مقایسهها، استخراج وزنهایی است که مجموع آنها برابر با یک بوده و میزان اهمیت هر معیار را نشان میدهد.
آنچه می خوانید
چرا وزن دهی در AHP اهمیت دارد؟
در بسیاری از روشهای ساده تصمیمگیری، فرض میشود همه معیارها اهمیت یکسانی دارند؛ اما در دنیای واقعی این فرض تقریباً همیشه اشتباه است. برای مثال، در انتخاب یک پروژه، ممکن است «هزینه» بسیار مهمتر از «زمان اجرا» باشد یا برعکس. اگر وزن دهی بهدرستی انجام نشود، نتیجه نهایی تصمیمگیری میتواند کاملاً گمراهکننده باشد.
AHP این مشکل را با تبدیل قضاوتهای کیفی به مقادیر کمی حل میکند. بهجای اینکه بگوییم «این معیار مهمتر است»، مشخص میکنیم چقدر مهمتر است. این موضوع باعث میشود خروجی تصمیمگیری قابل دفاع، شفاف و قابل تحلیل باشد.
روش های وزن دهی دقیق در AHP
1) روش حداقل مربعات

برای حل مساله فوق ، معادله لاگرانژی آن به صورت زیر در نظرگرفته می شود:
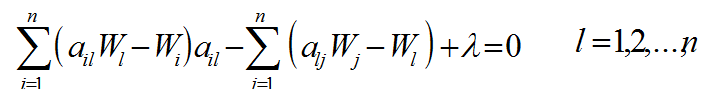
مثال روش حداقل مربعات
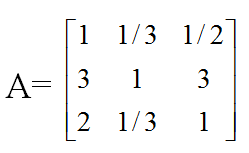
- نشان می دهیم ماتریس مقایسه ، ناسازگار است.
- وزن هر معیار را با روش حداقل مربعات به دست می آوریم:
اگر رابطه aik.akj=aij برای یکی از i,j,k ها برقرار نباشد ماتریس ناسازگار خواهد بود.

2) روش حداقل مربعات لگاریتمی

3) روش بردار ویژه
گام های روش:
- ماتریس A را تشکیل می دهیم.
- ماتریس (A – λI) را مشخص کنید.
- دترمینان ماتریس (A – λI) را محاسبه کرده و آن را مساوی صفر قرار داده و مقادیر λ را محاسبه کنید.
- بزرگترین λ را λmaxنامیده و آن را در رابطه A – λmax I) x W =0) قرار داده و با استفاده ازرابطه A – λmax I) x W =0) مقادیر Wi ها را محاسبه نمایید.

مثال روش بردار ویژه
برای ماتریس زیر، بردار و مقدار ویژه را محاسبه می کنیم.
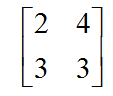
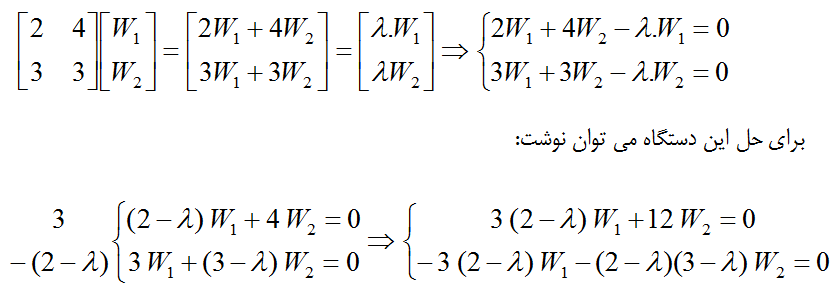

روش های وزن دهی تقریبی در AHP
1) مجموع سطری
ماتریس مقایسه زوجی زیر در دست است. با چهار روش ذکر شده بردار وزن را محاسبه می کنیم.
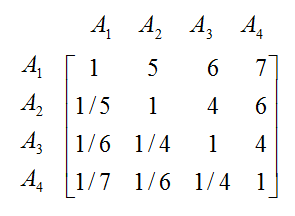
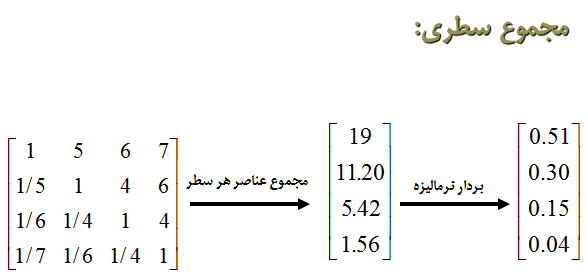
2) مجموع ستونی

3) میانگین حسابی
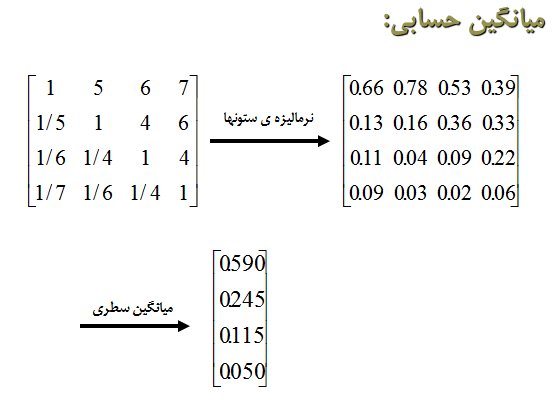
4) میانگین هندسی

مقایسههای زوجی در AHP چگونه انجام میشود؟
هسته اصلی وزن دهی در AHP، ماتریس مقایسههای زوجی است. در این ماتریس، هر معیار با سایر معیارها بهصورت دوتایی مقایسه میشود. تصمیمگیرنده مشخص میکند که یک معیار نسبت به معیار دیگر چه میزان اهمیت دارد. این اهمیت معمولاً با استفاده از مقیاس ۱ تا ۹ ساعتی (Saaty Scale) بیان میشود.
در این مقیاس:
- عدد ۱ به معنای اهمیت برابر دو معیار است
- عدد ۳ نشاندهنده اهمیت کم
- عدد ۵ اهمیت زیاد
- عدد ۷ اهمیت خیلی زیاد
- عدد ۹ اهمیت مطلق یک معیار نسبت به معیار دیگر
اعداد زوج (۲، ۴، ۶، ۸) برای حالتهای بینابینی استفاده میشوند. اگر معیار A نسبت به معیار B عدد ۵ بگیرد، در جهت معکوس مقدار ۱/۵ ثبت میشود. این ساختار باعث میشود ماتریس مقایسه زوجی خاصیت تقارن معکوس داشته باشد.
استخراج وزن معیارها در AHP
پس از تشکیل ماتریس مقایسههای زوجی، مرحله بعدی استخراج وزن معیارهاست. یکی از رایجترین روشها برای این کار، استفاده از بردار ویژه (Eigenvector) ماتریس است. در این روش، برداری محاسبه میشود که نشاندهنده اهمیت نسبی هر معیار است و سپس نرمالسازی میشود تا مجموع وزنها برابر با یک شود.
در عمل، برای مسائل کوچک و متوسط، میتوان از روشهای سادهتر مانند میانگین هندسی سطرها نیز استفاده کرد که نتایجی بسیار نزدیک به روش بردار ویژه ارائه میدهد. انتخاب روش محاسبه وزن بستگی به دقت موردنیاز و ابزار مورد استفاده (مانند اکسل یا نرمافزارهای تخصصی) دارد.
بررسی سازگاری وزن دهی در AHP
یکی از مزیتهای مهم AHP نسبت به بسیاری از روشهای وزندهی، امکان بررسی سازگاری قضاوتها است. از آنجا که مقایسهها توسط انسان انجام میشود، امکان وجود ناسازگاری منطقی وجود دارد. برای مثال، اگر معیار A از B مهمتر باشد و B از C مهمتر، انتظار میرود A از C هم مهمتر باشد.
AHP این موضوع را با شاخصهایی مانند نرخ ناسازگاری (Consistency Ratio) بررسی میکند. اگر این نرخ کمتر از ۰٫۱ باشد، قضاوتها قابل قبول در نظر گرفته میشوند. در غیر این صورت، لازم است مقایسهها بازبینی شوند تا وزن دهی معتبرتر شود.
کاربرد وزن دهی AHP در مسائل واقعی
وزن دهی در AHP در حوزههای مختلفی کاربرد دارد؛ از انتخاب پروژه و ارزیابی تأمینکنندگان گرفته تا برنامهریزی استراتژیک، انتخاب فناوری و حتی تصمیمگیریهای شخصی. دلیل این گستردگی کاربرد، انعطافپذیری بالا و قابلیت ترکیب AHP با سایر روشهاست.
در بسیاری از پژوهشها، AHP بهعنوان مرحله وزن دهی و سپس با روشهایی مانند TOPSIS، VIKOR یا ANP ترکیب میشود تا تصمیمگیری دقیقتری انجام شود. در این حالت، وزنهای استخراجشده از AHP نقش بسیار مهمی در نتیجه نهایی دارند.
وزن دهی در AHP با استفاده از نرمافزار و اکسل
در عمل، محاسبه وزن معیارها در AHP معمولاً بهصورت دستی انجام نمیشود و از ابزارهایی مانند نرمافزار Expert Choice، Super Decisions یا فایلهای اکسل استفاده میشود. این ابزارها فرآیند تشکیل ماتریس مقایسه زوجی، محاسبه وزنها و بررسی نرخ ناسازگاری را بهصورت خودکار انجام میدهند و احتمال خطای محاسباتی را کاهش میدهند.
در اکسل، وزن دهی در AHP معمولاً با محاسبه میانگین هندسی سطرهای ماتریس مقایسه زوجی انجام میشود. پس از نرمالسازی مقادیر، وزن نهایی هر معیار بهدست میآید و میتوان نرخ ناسازگاری را نیز بهصورت عددی بررسی کرد. این روش برای مسائل آموزشی و پروژههای دانشگاهی بسیار رایج است و در بسیاری از مقالات علمی نیز مورد استفاده قرار میگیرد.
استفاده از نرمافزار یا اکسل باعث میشود فرآیند وزن دهی شفافتر، قابل تکرار و مستند باشد؛ بهویژه در پروژههایی که تصمیمگیری باید برای دیگران قابل دفاع و قابل ارائه باشد. به همین دلیل، انتخاب ابزار مناسب نقش مهمی در دقت و اعتبار نتایج AHP دارد.
جمعبندی
وزن دهی در AHP روشی ساختارمند و منطقی برای تعیین اهمیت معیارها در مسائل تصمیمگیری چندمعیاره است. این روش با استفاده از مقایسههای زوجی، قضاوتهای انسانی را به وزنهای عددی تبدیل میکند و با بررسی سازگاری، اعتبار نتایج را افزایش میدهد. اگر وزن دهی بهدرستی انجام شود، AHP میتواند پایهای بسیار قدرتمند برای تصمیمگیریهای پیچیده و حساس فراهم کند.
