روش EDAS فازی

در دنیای پیچیده امروزی، تصمیم‌گیری‌های مدیریتی اغلب با چالش‌هایی همراه هستند که به دلیل وجود معیارهای متعدد و بعضاً متضاد، ماهیت چندمعیاره دارند. در چنین شرایطی، اتخاذ تصمیمی صحیح و کارآمد مستلزم استفاده از روش‌ها و ابزارهای نوین است.

روش EDAS (Evaluation of Distance from Average Solution) یکی از این ابزارها است که توسط M. Zavadskas, E. Zadunaite, R. Tamošaitiene, Ž. Žilinskaitė در سال 2012 معرفی و در سال 2016 توسط M. Keshavarz, E. Zavadskas, H. Amiri, Z. Zanon به صورت فازی تعمیم داده شد.

روش EDAS فازی، ابزاری قدرتمند برای حل مسائل تصمیم‌گیری چندمعیاره فازی (FCMDM) است که در آن اطلاعات با اعداد فازی که عدم قطعیت و ابهام را به طور ذاتی نشان می‌دهند، ارائه می‌شوند. این روش با اتکا به مفهوم فاصله از میانگین، گزینه‌های مختلف را بر اساس معیارهای فازی ارزیابی و رتبه‌بندی می‌کند.

در این مقاله، به آموزش جامع روش EDAS فازی می‌پردازیم. در ادامه، گام‌های این روش، مفاهیم کلیدی و کاربردهای آن به طور مفصل شرح داده خواهند شد. همچنین، مثال‌هایی از کاربرد این روش در مسائل مختلف ارائه می‌شود.

مفاهیم پایه EDAS فازی

در روش EDAS فازی، از مفاهیم مختلفی برای حل مسائل تصمیم‌گیری چندمعیاره فازی (FCMDM) استفاده می‌شود. در ادامه، به شرح برخی از این مفاهیم کلیدی می‌پردازیم:

1. اعداد فازی

اعداد فازی ابزاری ریاضی برای نشان دادن عدم قطعیت و ابهام در اطلاعات هستند. هر عدد فازی با یک تابع عضویت نشان داده می‌شود که مقادیر آن بین 0 و 1 قرار دارند. تابع عضویت نشان می‌دهد که هر مقدار در بازه مورد نظر چقدر با آن عدد فازی سازگار است.

انواع مختلفی از اعداد فازی وجود دارند، از جمله:

• اعداد فازی مثلثی: این نوع اعداد فازی با یک تابع عضویت مثلثی شکل نشان داده می‌شوند.
• اعداد فازی ذوزنقه ای: این نوع اعداد فازی با دو تابع عضویت نشان داده می‌شوند که هر کدام شکل ذوزنقه دارند.
• اعداد فازی بازه: این نوع اعداد فازی با یک بازه مشخص و تابع عضویت 1 در آن بازه نشان داده می‌شوند.

2. میانگین فازی

میانگین اعداد فازی با استفاده از روش‌های مختلفی مانند میانگین حسابی، هندسی یا ترکیبی از آنها محاسبه می‌شود.

• میانگین حسابی فازی: برای محاسبه میانگین حسابی اعداد فازی، ابتدا میانگین هر مؤلفه از اعداد فازی محاسبه شده و سپس عدد فازی جدیدی با آن مؤلفه‌ها ایجاد می‌شود.
• میانگین هندسی فازی: برای محاسبه میانگین هندسی اعداد فازی، ابتدا لگاریتم هر مؤلفه از اعداد فازی محاسبه شده و سپس میانگین لگاریتم‌ها محاسبه می‌شود. عدد فازی جدید با استفاده از آنتی‌لگاریتم میانگین لگاریتم‌ها ایجاد می‌شود.
• میانگین ترکیبی فازی: برای محاسبه میانگین ترکیبی اعداد فازی، از ترکیبی از روش‌های میانگین حسابی و هندسی استفاده می‌شود.

انتخاب روش مناسب برای محاسبه میانگین فازی به نوع اعداد فازی مورد استفاده و شرایط خاص مسئله بستگی دارد.

3. فاصله فازی

فاصله بین دو عدد فازی با استفاده از معیارهای مختلفی مانند فاصله هامینگ، اقلیدسی یا ترکیبی از آنها محاسبه می‌شود.

• فاصله هامینگ فازی: فاصله هامینگ بین دو عدد فازی، مجموع اختلاف مطلق هر مؤلفه از آن دو عدد فازی است.
• فاصله اقلیدسی فازی: فاصله اقلیدسی بین دو عدد فازی، ریشه دوم مجموع مربعات اختلاف هر مؤلفه از آن دو عدد فازی است.
• فاصله ترکیبی فازی: برای محاسبه فاصله ترکیبی فازی، از ترکیبی از روش‌های فاصله هامینگ و اقلیدسی استفاده می‌شود.

انتخاب روش مناسب برای محاسبه فاصله فازی به نوع اعداد فازی مورد استفاده و شرایط خاص مسئله بستگی دارد.

4. ایدآل‌های مثبت و منفی

ایدآل‌های مثبت و منفی در EDAS فازی، بهترین و بدترین مقادیر ممکن برای هر معیار را نشان می‌دهند. ایدآل‌های مثبت برای معیارهای مطلوب (معیارهایی که هرچه مقدار آنها بیشتر باشد بهتر است) و ایدآل‌های منفی برای معیارهای نامطلوب (معیارهایی که هرچه مقدار آنها کمتر باشد بهتر است) در نظر گرفته می‌شوند.

ایدآل‌های مثبت و منفی می‌توانند بر اساس دانش خبرگان، داده‌های تاریخی یا سایر اطلاعات مربوط به مسئله تعیین شوند.

5. وزن معیارها

وزن معیارها نشان‌دهنده اهمیت نسبی هر معیار در فرایند تصمیم‌گیری است. معیارهای مهم‌تر، وزن‌های بیشتری به آنها اختصاص داده می‌شود. انتخاب وزن معیارها می‌تواند به روش‌های مختلفی مانند روش AHP، روش دلفی یا روش خوشه‌بندی انجام شود. درک مفاهیم پایه EDAS فازی برای استفاده مؤثر از این روش در حل مسائل FCMDM ضروری است.

در ادامه این مقاله، به سایر مفاهیم و گام‌های این روش خواهیم پرداخت.

مزایای EDAS فازی

روش EDAS فازی مزایای متعددی دارد که از جمله آنها می‌توان به موارد زیر اشاره کرد:

• قابلیت ‌مدیریت عدم قطعیت: EDAS فازی به طور ذاتی عدم قطعیت و ابهام را در اطلاعات مدیریت می‌کند. این امر در بسیاری از مسائل دنیای واقعی که با داده‌های ناقص یا غیر دقیق سروکار دارند، حائز اهمیت است.
• سادگی و سهولت استفاده: EDAS فازی روشی نسبتاً ساده و قابل فهم است که به راحتی می‌توان آن را در عمل پیاده‌سازی کرد. این امر آن را به ابزاری مناسب برای تصمیم‌گیرندگانی تبدیل می‌کند که دانش تخصصی در زمینه روش‌های تصمیم‌گیری چندمعیاره ندارند.
• قدرت تفکیک: EDAS فازی قدرت تفکیک بالایی دارد و می‌تواند گزینه‌های مختلف را به طور دقیق از یکدیگر تفکیک کند. این امر در مسائلی که گزینه‌های بسیار نزدیک به یکدیگر هستند، حائز اهمیت است.
• قابلیت انعطاف‌پذیری: EDAS فازی روشی انعطاف‌پذیر است که می‌توان از آن در مسائل مختلف FCMDM استفاده کرد. این روش می‌تواند با انواع مختلف اعداد فازی، معیارها و ترجیحات تصمیم‌گیرنده سازگار شود.

کاربردهای روش EDAS فازی

روش EDAS فازی در طیف گسترده‌ای از مسائل FCMDM کاربرد دارد، از جمله:

• انتخاب تامین کننده: انتخاب بهترین تامین کننده برای یک محصول یا خدمات.
• انتخاب مکان: انتخاب بهترین مکان برای احداث یک تاسیسات جدید.
• انتخاب پروژه: انتخاب بهترین پروژه برای سرمایه‌گذاری.
• ارزیابی عملکرد: ارزیابی عملکرد کارکنان، دانش‌آموزان یا سایر افراد.
• حل مسئله: حل مسائل پیچیده با چندین معیار متضاد.

EDAS فازی به دلیل مزایای متعدد و کاربردهای گسترده، به ابزاری محبوب برای تصمیم‌گیری در شرایط عدم قطعیت تبدیل شده است.

مراحل روش EDAS فازی

این روش با استفاده از مفهوم فاصله از میانگین، گزینه‌های مختلف را بر اساس معیارهای فازی ارزیابی و رتبه‌بندی می‌کند. گام‌های روش EDAS فازی به شرح زیر است:

مرحله 1: ماتریس ارزیابی را بسازید که می تواند به صورت زیر نمایش داده شود:

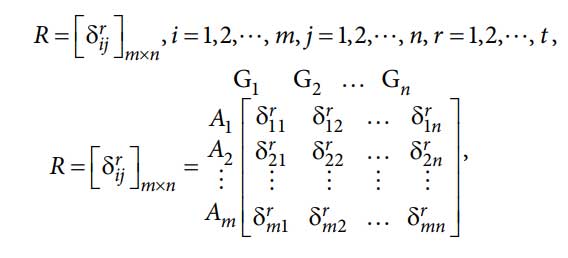
مرحله 2: عادی سازی ماتریس ارزیابی Rij برای معیارهای مثبت و منفی

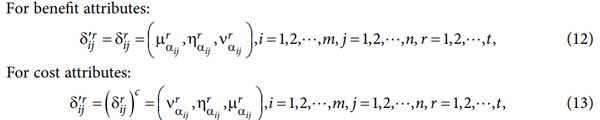
مرحله 3: با توجه به ماتریس تصمیم‌گیری rij و بردار وزن خبرگان، می‌توان rij کلی را با استفاده از عملگر PFWA استخراج کرد که نتایج محاسبات را می‌توان به صورت زیر ارائه کرد.

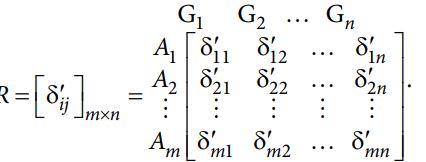
مرحله 4: مقدار راه حل متوسط ​​(AV) را بر اساس تمام ویژگی های پیشنهادی محاسبه کنید:

مرحله 5: با توجه به نتایج حل میانگین (AV) می‌توان فاصله مثبت از میانگین (PDA) و فاصله منفی از میانگین (NDA) را با استفاده از فرمول زیر محاسبه کرد:

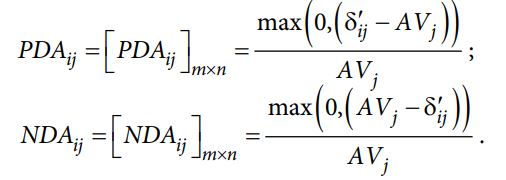
برای راحتی، می توانیم از تابع امتیاز PFN ارائه شده در تعریف 3 برای تعیین نتایج PDA و NDA به صورت زیر استفاده کنیم:

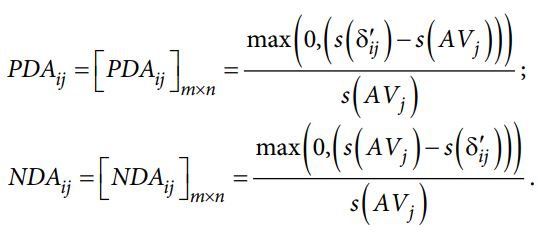
مرحله 6: مقادیر SPi و SNi را که بیانگر مجموع وزنی PDA و NDA است محاسبه کنید، فرمول محاسباتی به صورت زیر ارائه می شود:

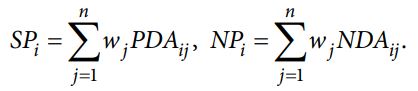
مرحله 7: نتایج معادله (20) را می توان به صورت زیر نرمال کرد:

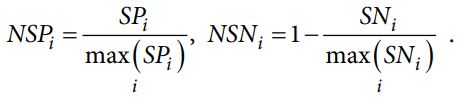
مرحله 8: مقادیر امتیاز ارزیابی (AS) را بر اساس NSPi و NSNi هر جایگزین محاسبه کنید.

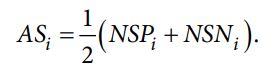
مرحله 9. با توجه به نتایج محاسباتی AS، می‌توانیم همه گزینه‌ها را رتبه‌بندی کنیم، هر چه مقدار AS بزرگتر باشد، بهترین جایگزین انتخاب شده خواهد بود.

مثال روش EDAS فازی

این مثال از مقاله EDAS METHOD FOR MULTIPLE CRITERIA GROUP DECISION MAKING WITH PICTURE FUZZY INFORMATION AND ITS APPLICATION TO GREEN SUPPLIERS SELECTIONS استخراج شده است.

پنج تامین کننده سبز(A=1،2،3،4،5) انتخاب شده اند و چهار ویژگی برای ارزیابی این تامین کنندگان سبز وجود دارد: G1 عامل قیمت است. G2 عامل تحویل است. G3 عوامل محیطی است. G4 فاکتور کیفیت محصول است.

پنج تامین کننده سبز ممکن (A=1،2،3،4،5) باید با PFN با چهار معیار اوزان معیارها w = (0.25،0.18،0.35،0.22)، وزن خبرگانE = (0.35،0.2،0.45) ارزیابی شوند. ماتریس ارزیابی در جداول 1-3 فهرست شده است.

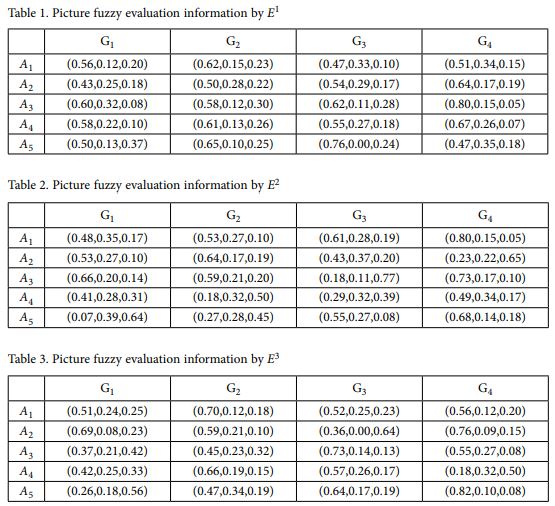
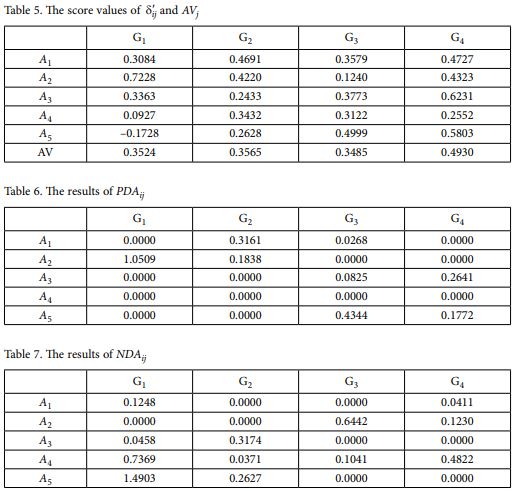
با توجه به ماتریس تصمیم گیری و بردار وزن متخصص، rij کلی را با استفاده از عملگر تجمع PFWA محاسبه می کنیم، نتایج محاسبات را می توان در جدول 4 ارائه کرد.

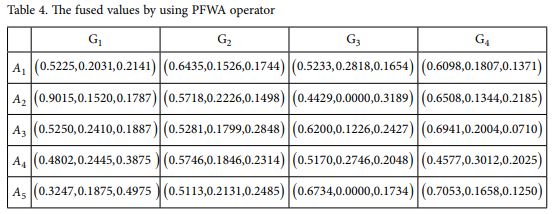
با توجه به جدول 4، می توانیم مقدار جواب متوسط ​​(AV) را بر اساس تمام ویژگی های پیشنهادی با فرمول (17) بدست آوریم:

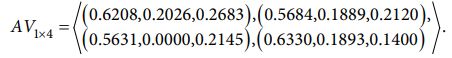
با توجه به نتایج حل میانگین (AV) می توان فاصله مثبت از میانگین (PDA) و فاصله منفی از میانگین (NDA) را با استفاده از فرمول (20) و (21) که در جداول 5-7 آورده شده است محاسبه کرد.

مقادیر SPi و SNi را با معادله (23) و بردار وزنی صفات w = (0.25، 0.18، 0.35، 0.22) محاسبه کنید، می توانیم نتایج را به صورت زیر بدست آوریم:

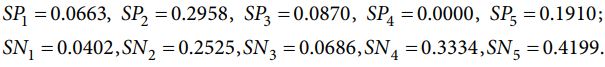
نتایج مرحله 6 را می توان با فرمول (24) نرمال کرد و نتایج به شرح زیر است:

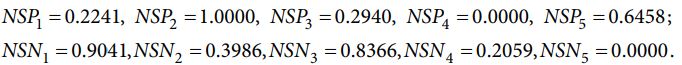
بر اساس NSPi و NSNi هر جایگزین برای محاسبه مقادیر AS.

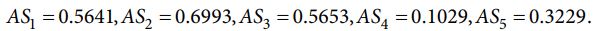
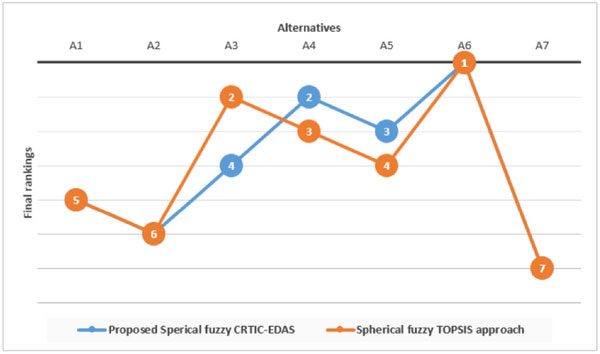
با توجه به نتایج محاسباتی AS، می‌توانیم همه گزینه‌ها را رتبه‌بندی کنیم، هر چه مقدار AS بیشتر باشد، بهترین جایگزین انتخاب شده خواهد بود. بدیهی است که رتبه همه جایگزین ها A2>A3>A1>A5>A4 است و A2 بهترین تامین کننده سبز است.

نتیجه گیری

روش EDAS فازی ابزاری قدرتمند و کارآمد برای حل مسائل FCMDM است. این روش به طور ذاتی عدم قطعیت و ابهام را در اطلاعات مدیریت می‌کند و از مزایای دیگری مانند سادگی، قدرت تفکیک و انعطاف‌پذیری برخوردار است. EDAS فازی در طیف گسترده‌ای از مسائل کاربرد دارد و می‌تواند به تصمیم‌گیرندگان در اتخاذ تصمیمات صحیح و کارآمد کمک کند.

در این مقاله، به آموزش جامع روش EDAS فازی پرداخته شد. با این حال، برای درک عمیق‌تر این روش و استفاده مؤثر از آن در حل مسائل واقعی، مطالعه منابع تخصصی و انجام تمرینات عملی ضروری است.

همچنین، توجه به این نکته ضروری است که EDAS فازی تنها یکی از روش‌های متعدد برای حل مسائل FCMDM است. انتخاب روش مناسب برای یک مسئله خاص به عوامل مختلفی مانند نوع مسئله، در دسترس بودن اطلاعات و ترجیحات تصمیم‌گیرنده بستگی دارد.

سوالات متداول در مورد روش EDAS فازی