فایل اکسل ahp چند سطحی

توضیحات

فایل اکسل AHP چند سطحی؛ ابزار پیشرفته محاسبات سلسله‌مراتب پیچیده

زمانی که مسئله تصمیم‌گیری شما از حالت ساده خارج شده و دارای چندین لایه از زیرمعیارهاست، محاسبات دستی تقریباً غیرممکن و بسیار خطا‌پذیر می‌شود. فایل اکسل AHP چند سطحی به عنوان یک راهکار حرفه‌ای، به شما اجازه می‌دهد تا ساختارهای درختی با سطوح مختلف را با دقت ۱۰۰٪ مدل‌سازی کنید. در این ابزار، تمامی روابط بین معیارهای اصلی و زیرمعیارها فرمول‌نویسی شده است تا شما بدون درگیری با پیچیدگی‌های ریاضی، بر تحلیل نتایج روش AHP چند سطحی تمرکز کنید.

ویژگی‌های فنی و محاسباتی این فایل اکسل

این فایل اکسل AHP چند سطحی به گونه‌ای طراحی شده است که تمامی نیازهای یک پژوهش علمی را پوشش می‌دهد:

• محاسبه وزن‌های ترکیبی (Global Weights): اصلی‌ترین ویژگی این ابزار، ضرب خودکار وزن‌های نسبی هر سطح در سطح بالادستی برای استخراج اهمیت نهایی زیرمعیارها است. این دقیقاً همان بخشی است که در آموزش وزن دهی در AHP به عنوان چالش اصلی محققان معرفی کردیم.

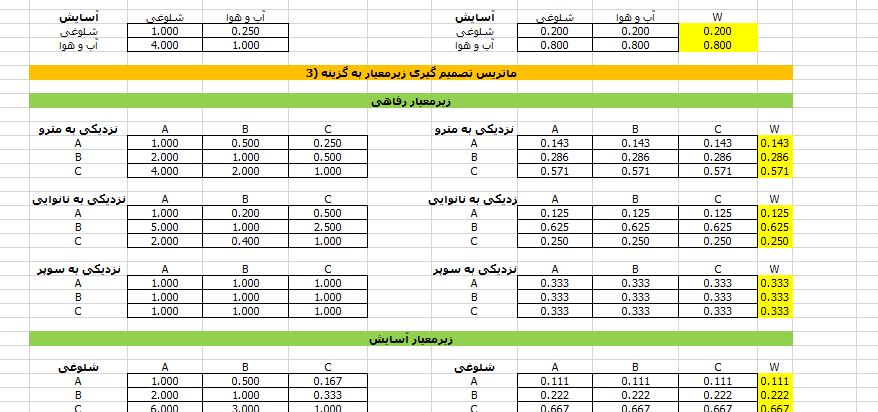
• کنترل نرخ ناسازگاری در هر خوشه: در این فایل اکسل AHP چند سطحی، برای هر ماتریس مقایسات زوجی (چه در سطح معیارها و چه زیرمعیارها)، یک بخش مجزا برای محاسبه نرخ ناسازگاری در AHP تعبیه شده است تا از اعتبار تک‌تک بخش‌های مدل اطمینان حاصل کنید.

• رتبه‌بندی نهایی گزینه‌ها: پس از تعیین وزن‌ها، این فایل به شما اجازه می‌دهد گزینه‌ها را نسبت به آخرین سطح زیرمعیارها مقایسه کرده و اولویت‌بندی نهایی را در قالب نمودارهای بصری دریافت کنید.

چرا استفاده از فایل اکسل AHP چند سطحی الزامی است؟

در اکثر پروژه‌های تصمیم‌گیری چندمعیاره (MCDM)، اشتباه در انتقال وزن از سطوح بالاتر به پایین‌تر باعث می‌شود که نتایج نهایی کاملاً اشتباه از آب درآیند. با استفاده از این فایل اکسل AHP چند سطحی، این ریسک به طور کامل از بین می‌رود. فرمول‌نویسی زنجیره‌ای این فایل به گونه‌ای است که با تغییر یک عدد در بالاترین سطح، تمامی وزن‌های سطوح پایین‌تر به صورت خودکار به‌روزرسانی می‌شوند. این قابلیت برای محققانی که نیاز به انجام تحلیل حساسیت در بخش آمار و تحلیل داده دارند، یک مزیت حیاتی است.

علاوه بر دقت، کاربری آسان این فایل اکسل AHP چند سطحی باعث شده تا جایگزین مناسبی برای نرم‌افزارهای پیچیده باشد. اگر شما مطابق با اصول روش AHP پیش رفته باشید، تنها کافیست داده‌های پرسشنامه خود را در خانه‌های مشخص شده وارد کنید. این محصول با استانداردهای آموزشی آکادمی نرم‌افزار فرابگیر کاملاً منطبق است و به شما کمک می‌کند تا پایان‌نامه یا مقاله خود را در رشته‌های آموزش مدیریت و مهندسی صنایع با بالاترین کیفیت ممکن ارائه دهید.

💡 پیشنهاد ویژه: اگر پروژه شما علاوه بر چند سطحی بودن، به صورت گروهی نیز انجام می‌شود، توصیه می‌کنیم از پکیج ترکیبی فایل اکسل AHP گروهی و چند سطحی استفاده کنید تا تمامی ابعاد مسئله را پوشش دهید.