مثال روش AHP یا (Analytical Hierarchy process-AHP) که به فرایند تحلیل سلسه مراتبی مشهور است، یکی از کارآمد ترین تکنیک های تصمیم گیری می باشد که بر اساس مقایسه های زوجی بنا نهاده شده و اولین بار توسط توماس ال ساعتی در سال 1980 مطرح شد. این روش امکان بررسی سناریوهای مختلف را به مدیران می دهد.
فرآیند تحلیل سلسله مراتبی (AHP) برای تصمیمگیری با معیارهای چندگانه بهکار میرود زیرا با استفاده از این مدل میتوان معیارها را به صورت سلسله مراتبی با هم مقایسه کرد. این معیارها میتوانند کمی و یا کیفی باشند. تحلیل سلسله مراتبی (AHP) توسط توماس ال، ساعتی در دهه 1970 ارائه شده است. این روش بر اساس مقایسات زوجی انجام میشود.
به عنوان مثال میخواهیم چندین مکان را برای احداث سالن ورزشی با هم مقایسه کنیم. این مکانها دارای ویژگیهای متفاوت هستند. تمام معیارهایی که برای انتخاب یک سالن ورزشی مناسب باید در نظر گرفته شود را بررسی کردهایم.
میخواهیم با استفاده از این معیارها زمینهای مناسب را شناسایی و اولویت بندی کنیم. برای اینکار از روش تحلیل سلسله مراتبی استفاده میکنیم و با توجه به نظرات خبرگان تصمیمگیری چندمعیاره را انجام میدهیم. در ادامه مثالی از روش AHP برای شما آورده شده است.
مثال روش AHP مثال روش AHP مثال روش AHP مثال روش AHP
مثال روش AHP
تصور کنید که از بین سه اتومبیل A,B,C یکی را انتخاب کنیم چهار معیار: راحتی، قیمت، مصرف سوخت، مدل مطرح می باشد .حل این مثال را طی قدم های زیر تشریح می کنیم:
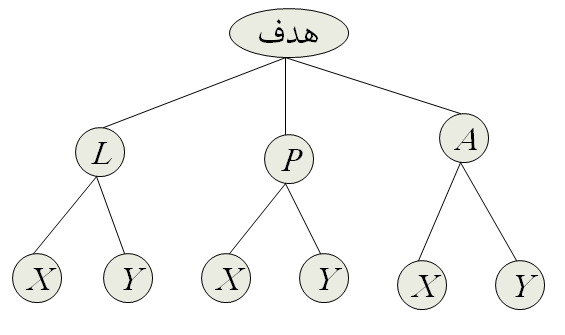
1) رسم سلسله مراتب
ابتدا سلسله مراتب را بر اساس معیارها رسم می نماییم.
2) جمع آوری نظرات خبرگان
پس از تهیه پرسش نامه و ارائه آن به خبرگان، بر اساس جدول ترجیحات نظرات آن ها جمع آوری می گردد.
| ترجیحات (قضاوت شفاهی) | مقدار عددی | |
| کاملا مرجح یا کاملا مهم تر یا کاملا مطلوب تر | Extremely preferred | 9 |
| ترجیح با اهمیت یا مطلوبیت خیلی قوی | Very strongly preferred | 7 |
| ترجیح با اهمیت یا مطلوبیت قوی | Strongly preferred | 5 |
| کمی مرجح یا کمی مهم تر یا کمی مطلوب تر | Moderately preferred | 3 |
| ترجیح یا اهمیت یا مطلوبیت یکسان | Equally preferred | 1 |
| ترجیحات بین فواصل قوی | 8،6،4،2 | |
3) محاسبه اوزان زیر معیارها
جهت محاسبه وزن ها ابتدا ماتریس های مقایسه زوجی را برای هر 4 شاخص: راحتی، قیمت، مصرف، مدل و همچنین خود اتومبیل ها نسبت به هم تشکیل می دهیم.
مثال روش AHP مثال روش AHP مثال روش AHP مثال روش AHP
| Aاتومبیل | Bاتومبیل | Cاتومبیل | |
| Aاتومبیل | 1 | 2 | 8 |
| Bاتومبیل | 1/2 | 1 | 6 |
| Cاتومبیل | 1/8 | 1/6 | 1 |
| A اتومبیل | B اتومبیل | C اتومبیل | |
| Aاتومبیل | 1 | 1/3 | 1/4 |
| B اتومبیل | 3 | 1 | 1/2 |
| C اتومبیل | 4 | 2 | 1 |
| A اتومبیل | B اتومبیل | C اتومبیل | |
| Aاتومبیل | 1 | 1/4 | 1/6 |
| B اتومبیل | 4 | 1 | 1/3 |
| C اتومبیل | 6 | 3 | 1 |
| A اتومبیل | B اتومبیل | C اتومبیل | |
| A اتومبیل | 1 | 4 | 4 |
| B اتومبیل | 3 | 1 | 7 |
| C اتومبیل | 1/4 | 1/7 | 1 |
نکته: عناصر زیر قطر ماتریس برعکس عناصر بالای ماتریس می باشند. مثلا اگر A به B در بالای ماتریس 2 باشد B به A در زیر ماتریس 1/2 خواهد بود. برای محاسبه اوزان از روش میانگین سطری استفاده می کنیم. گام های زیر را برای هر 4 ماتریس انجام می دهیم تا وزن هر کدام بدست آید.
مثال روش AHP مثال روش AHP مثال روش AHP مثال روش AHP
مقادیر هر یک از ستون ها را با هم جمع می کنیم.
| راحتی | A اتومبیل | B اتومبیل | C اتومبیل |
| Aاتومبیل | 1 | 2 | 8 |
| B اتومبیل | 1/2 | 1 | 6 |
| Cاتومبیل | 1/8 | 1/6 | 1 |
| جمع هر ستون | 13/8 | 19/6 | 15 |
گام دوم: تقسیم هر عنصر از ماتریس به جمع کل ستون همان عنصر( نرمالایز کردن)
| راحتی | A اتومبیل | B اتومبیل | C اتومبیل |
| Aاتومبیل | 8/13 | 12/19 | 8/15 |
| B اتومبیل | 4/13 | 6/19 | 6/15 |
| Cاتومبیل | 1/13 | 1/19 | 1/15 |
گام سوم: محاسبه متوسط عناصر در هر سطر
| راحتی | Aاتومبیل | B اتومبیل | C اتومبیل | متوسط سطر |
| Aاتومبیل | 0.615 | 0.631 | 0.533 | 0.593 |
| B اتومبیل | 0.308 | 0.316 | 0.400 | 0.341 |
| Cاتومبیل | 0.077 | 0.053 | 0.067 | 0.066 |
| جمع کل | 1 | 1 | 1 | 1 |
تمامی گام های فوق را برای 3 شاخص باقیمانده قیمت، مصرف و مدل انجام داده و برای هر کدام از آن ها نیز متوسط سطر را بدست می آوریم که حاصل آن در جدول زیر آورده شده است.
| اوزان | قیمت | مصرف | مدل |
| A اتومبیل | 0.123 | 0.087 | 0.449 |
| B اتومبیل | 0.320 | 0.274 | 0.495 |
| C اتومبیل | 0.557 | 0.639 | 0.057 |
4) محاسبه اوزان معیارها
حال در که وزن هر کدام از زیر معیارهای قیمت، مصرف، مدل و راحتی محاسبه شد زمان آن رسیده که معیار ها نیز با هم مقایسه شوند.
| معیارها | قیمت | مصرف | راحتی | مدل |
| قیمت | 1 | 3 | 2 | 2 |
| مصرف | 1/3 | 1 | 1/4 | 1/4 |
| راحتی | 1/2 | 4 | 1 | 1/2 |
| مدل | 1/2 | 4 | 2 | 1 |
مانند قبل برای این ماتریس هم گام ها را ادامه می دهیم و اوزان معیارها به صورت زیر بدست می آید:
0.398 قیمت | 0.085 مصرف | 0.218 راحتی |0.299 مدل
مثال روش AHP مثال روش AHP مثال روش AHP مثال روش AHP
5) محاسبه وزن نهایی
حال با ضرب وزن هر کدام از زیر معیارها در معیار اصلی آن وزن کلی را بدست می آوریم:
وزن نهائی اتومبیل A: 0.398*0.123+0.085*0.087+0.218*0.593+0.299*0.0.449=0.320
وزن نهائی اتومبیل B: 0.398*0.320+0.085*0.274+0.218*0.341+0.299*0.495=0.373
وزن نهائی اتومبیل C: 0.398*0.557+0.085*0.639+0.218*0.066+0.299*0.057=0.307
با توجه به اوزان بدست آمده اولویت ها به ترتیب B>C>A خواهد بود.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.