
تحلیل پوششی داده ها (DEA)
در سال 1957 فارل با استفاده از روشی مانند اندازه گیری کارایی در مباحث مهندسی اقدام به اندازه گیری کارایی برای یک واحد تولیدی نمود. روش وی دارای یک ورودی و یک خروجی بود و او در ارائه روشی که در برگیرنده ورودی ها و خروجی های متعدد باشد موفق نبود. چارنز،کوپر و رودز دیدگاه فارل را توسعه داده و مدلی را ارائه کردند که توانایی اندازه گیری کارایی با چند ورودی و چند خروجی را داشت.
در سال 1976 مدل تحلیل پوششی داده ها اولین بار در رساله دکتری ” ادوارد رودز” به راهنمایی” کوپر” با عنوان “ارزیابی پیشرفت تحصیلی دانش آموزان مدارس ملی آمریکا” مورد استفاده قرار گرفت و در سال 1978 در مقاله ای تحت عنوان “اندازه گیری واحدهای تصمیم گیرنده ”ارائه شد.
تحلیل پوششی داده ها چیست؟
تحلیل پوششی داده ها یک روش برنامه ریزی خطی برای تعیین کارایی نسبی عملکرد واحدهای تصمیم گیرنده (DMU) یک سیستم است. از شرایط واحدهای مورد ارزیابی(واحد تصمیم گیری) این است که با صرف تعدادی ورودی، تعداد معینی خروجی را تولید می کنند.
نکته قابل توجه این است که در یک مساله تصمیم گیری می توان با شبیه سازی گزینه ها و معیارهای مورد ارزیابی به عنوان واحدها و ورودی ها و خروجی های آن ها از تکنیک در راستای رتبه بندی گزینه ها با در نظر گرفتن معیارهای مورد نظر استفاده کرد.
به عبارت دیگر در مسائل مربوط به تحلیل پوششی داده ها، مفهوم کارایی لزوماً به معنی کارایی یک واحد فیزیکی نخواهد بود، بلکه می توان با تعریف کارایی برای یک واحد مجازی به هدف مورد نظر دست یافت. براساس این روش مدیر می تواند با استفاده از بهترین واحد تصمیم گیری برای سایر واحدها الگوگیری نماید.
کاربردهای تحلیل پوششی داده ها
از زمان انتشار این روش تاکنون تحلیل پوششی داده ها در زمینه های بسیار متنوعی برای ارزیابی کارآیی نسبی واحدهای تصمیم گیری همچون سنجش و مقایسه کارآیی شعب بانک ها، بیمه ها، مدارس و دانشگاه ها، بیمارستان ها، فروشگاه های زنجیره ای، سهام های موجود در یک صنعت در بازار سرمایه، صندوق های سرمایه گذاری مشترک، پایگاه های نظامی، مکان یابی شهرها و پایتخت ها تجاری و سیاسی، ارزیابی خودروسازان مختلف، مسائل جایابی و چیدمان، آژانس های خدمات مسافرتی و هوایی و ده ها زمینه دیگر به کار رفته است و به مرور زمان بر کاربرهای آن از علوم مختلف اقتصادی – مهندسی گرفته تا پزشکی و زیست شناختی افزوده می گردد.
روش تحلیل پوششی داده ها (DEA) اگرچه ابتدا به عنوان یکی از روش های ارزیابی کارآیی مطرح گردید ولی با توجه به کاربردهای فراوان بویژه در امر تصمیم گیری امروزه به عنوان ابزاری قدرتمند در زمینه تصمیم گیری و سنجش کارآیی واحد های تصمیم گیری مطرح می باشد.
دو مشخصه اصلی روش تحلیل پوششی داده ها
استفاده از الگوی DEA، برای ارزیابی نسبی واحدها، نیازمند تعیین دو مشخصه اساسی دیدگاه الگو و بازده به مقیاس الگو می باشد که در ادامه به تشریح هریک پرداخته می شود.
الف) دیدگاه الگو
- دیدگاه ورودی: در صورتی که در فرآیند ارزیابی با ثابت نگه داشتن سطح خروجی ها سعی در حداقل سازی ورودی ها داشته باشیم ماهیت الگو مورد استفاده ورودی است.
- دیدگاه خروجی: در صورتی که در فرآیند ارزیابی با ثابت نگه داشتن سطح ورودی ها سعی در حداقل سازی خروجی داشته باشیم ماهیت الگو مورد استفاده خروجی است.
در الگوی DEA، با دیدگاه ورودی به دنبال به دست آوردن ناکارایی فنی به عنوان نسبتی می باشیم که بایستی در ورودی ها کاهش داده شود تا خروجی بدون تغییر بماند و واحد در مرز کارایی قرار گیرد.
در دیدگاه خروجی به دنبال نسبتی هستیم که باید خروجی ها افزایش یابند بدون اینکه تغییری در ورودی ها به وجود آید تا واحد مورد نظر به مرز کارایی برسد.
علت انتخاب دیدگاه برای یک الگو DEA در ارزیابی نسبی عملکرد واحدهایی است که در بعضی موارد مدیریت واحد هیچ کنترلی بر میزان خروجی ندارد و مقدار آن از قبل مشخص و ثابت می باشد.
برعکس در بعضی از موارد میزان ورودی ثابت و مشخص است و میزان تولید ( خروجی) متغیر است و در چنین شرایطی، دیدگاه خروجی مناسب می باشد. در نهایت انتخاب دیدگاه ورودی و خروجی بر اساس میزان کنترل مدیر بر هر یک از ورودی ها و خروجی ها تعیین می گردد.
ب) بازده به مقیاس الگو
بازده به مقیاس بیانگر پیوند بین تغییرات ورودی ها و خروجی ها یک سیستم می باشد. یکی از توانایی های روش DEA کاربرد الگوهای مختلف متناظر با بازده به مقیاس های متفاوت و همچنین اندازه گیری بازده به مقیاس واحدهاست.
تحلیل پوششی داده ها
این الگو دارای دو نوع می باشد:
- بازده به مقیاس ثابت (CCR): یعنی هر مضربی از ورودی ها همان مضرب از خروجی ها را تولید می کند. الگوی CCR بازده به مقیاس واحد ها را ثابت فرض می کند. بنابراین واحد های کوچک و بزرگ باهم مقایسه می شوند.
- بازده به مقیاس متغیر(BCC): یعنی هر مضربی از ورودی ها می تواند همان مضرب از خروجی ها یا کمتر از آن و یا بیشتر از آن را تولید کند.
- الگوی BCC بازده به مقیاس را متغیر فرض می کند.
در الگوی CCR مقادیر بدست آمده برای کارایی در دو دیدگاه مساوی هستند ولی در مدل BCC این مقادیر متفاوت هستند.
بازده به مقیاس ثابت (CCR)
این الگو دارای بازده ثابت به مقیاس است و سعی دارد با انتخاب وزن های بهینه برای متغیر های ورودی و خروجی واحد تحت بررسی، کسر کارایی این واحد (واحد صفر) را به گونه ای بیشتر کند که کارایی سایر واحدها از حد بالای یک تجاوز نکند.
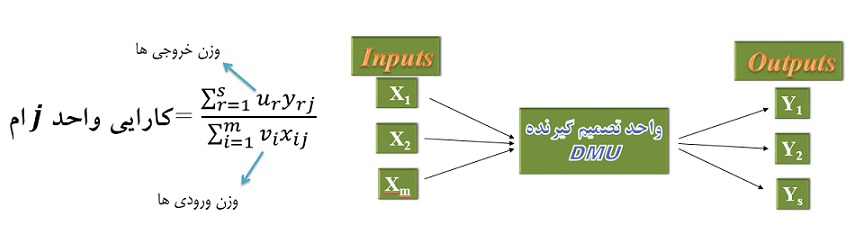
در این مدل ورودی xij و خروجی Yij اعداد مثبت بوده و مقادیر Ur و Vr اوزان مجهول و به عبارت دیگر متغیرهای تصمیم مدل برنامه ریزی می باشند.
در این مدل با تخصیص وزن ها به صورت ضرایب به هرکدام از ورودی ها و خروجی ها، ورودی های و خروجی های چندگانه به یک ورودی و خروجی مجازی تبدیل می شود.
مدل مضربی و ثانویه CC
مدل اولیه DEA یک برنامه کسری خطی است که باید به مدل خطی تبدیل شود تا بتوان به روش های برنامه ریزی خطی آن را حل کرد. مدل CCR را با استفاده از روش های پیشنهادی چانز می توان به قالب برنامه ریزی خطی تبدیل کرد.
روش تحلیل پوششی داده ها
برای حداکثر کردن مقدار مقدار یک عبارت کسری کافی است مخرج کسر را معادل یک عدد ثابت در نظر گرفته و صورت کسر را حداکثر نمود.
در مدل CCR مخرج کسر تابع هدف را برابر یک در نظر گرفته و مدل برنامه ریزی خطی به این صورت نوشته می شود.
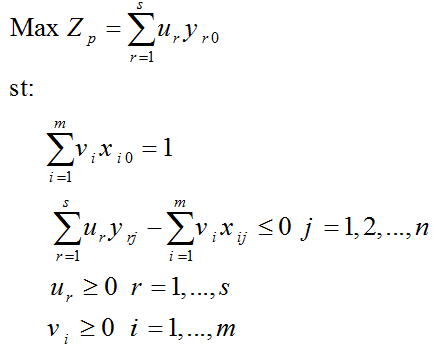

در ارزیابی واحد تصمیم گیری p ام جواب بهینه نشان دهنده ترکیبی از واحدهای تصمیم گیری با ضرایب jλ است که این ترکیب با نسبتی از ورودی های واحد p ام بتواند ستاده های واحد p ام را تولید کند.
تحلیل پوششی داده ها (DEA) تحلیل پوششی داده ها (DEA) تحلیل پوششی داده ها (DEA) تحلیل پوششی داده ها (DEA)
دو مشکل در بکارگیری مدلهای کلاسیک (مدل های CCR) رخ می دهد:
- ضعف قدرت تفکیک
- توزیع غیرواقعی وزن به ورودیها و خروجی های مدل
بازده به مقیاس متغیر (BCC)
درسال 1984 بنکر چارلز و کوپر با تغییر در مدل CCR مدل جدید را عرضه کردند. که با توجه به حروف اول نام آنان به مدل BCC شهرت یافت.
مدل BCC مدلی از انواع مدل های تحلیل پوششی داده هاست که در ارزیابی کارایی نسبی واحدهایی با بازده متغیر نسبت به مقیاس می پردازد.
مدل مضربی و ثانویه BCC
به این معنی که افزایش خروجی بیشتر یا کمتر از نسبت افزایش در ورودی است. مدل BCC برای ارزیابی کارایی واحد تحت بررسی p به صورت زیر می باشد.
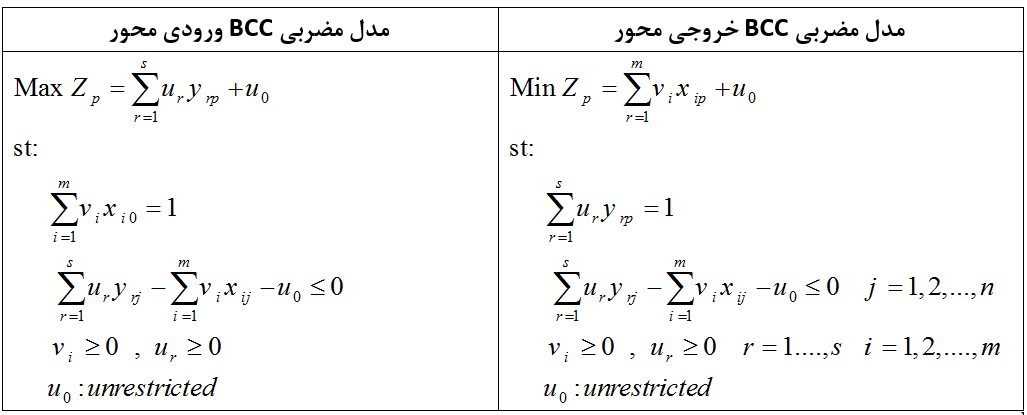
روش DEA
در این مدل، علامت متغیر u0 که یک متغیر آزاد است، نشانگر نوع بازده به مقیاس تولید واحد مورد ارزیابی است. فرض بازدهی ثابت نسبت به مقیاس تنها در صورتی قابل اعمال است که بنگاه ها در مقایسه بهینه عمل کنند. مسایل متفاوتی از قبیل اثرات ناشی از رقابت، محدودیت ها و غیره موجب می شود بنگاه ها در مقیاس بهینه عمل نکنند.
تحلیل پوششی داده ها (DEA) تحلیل پوششی داده ها (DEA) تحلیل پوششی داده ها (DEA) تحلیل پوششی داده ها (DEA)
الگوی BCC، بازده به مقیاس را متغیر فرض می کند.
مدل های بازده به مقیاس ثابت واحدهای کارای کمتری را در بر می گیرد و محدودکننده تر از مدل بازده به مقیاس متغیر می باشد. لذا می توان گفت بازده به مقیاس واحد ارزیابی:
- کاهشی است اگر u0<0
- ثابت است اگرu0=0
- افزایشی است اگر u0>0
مدل های ثانویه BCC در حالت خروجی محور و ورودی محور به صورت جدول می باشند.(D

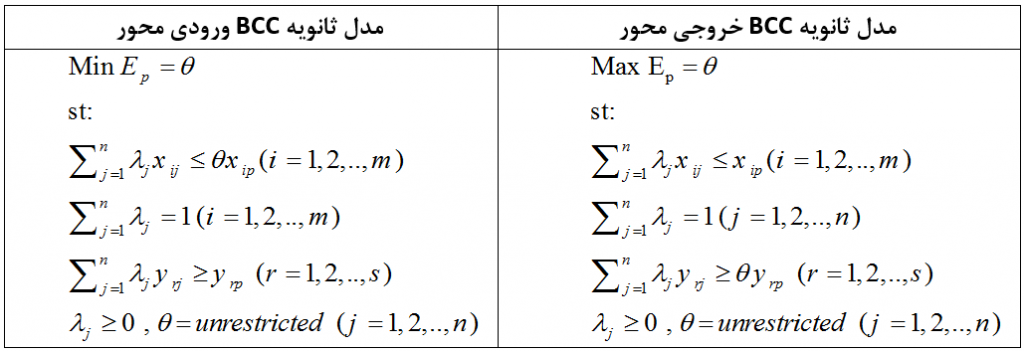
در دیدگاه خروجی ما سعی در حداکثر سازی خروجی با ثابت ماندن ورودی ها داریم.
بله، کجا خلاف این مطلب گفته شده؟