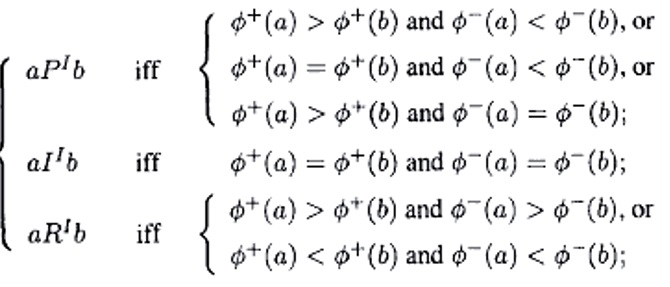آموزش جامع روش PROMETHEE

روش PROMETHEE که مخفف Preference Ranking Organization Method for Enrichment Evaluations است، در دهه ۸۰ میلادی به عنوان پاسخی به نیازهای پیچیده تصمیم‌گیری معرفی شد. این متد برخلاف روش‌های کلاسیک که گزینه‌ها را مستقیماً امتیازدهی می‌کنند، بر پایه مفهوم «رتبه‌بندی برتری» استوار است. در واقع، پرومتی به دنبال این است که با مقایسه دو به دوی گزینه‌ها، شدت ترجیح یکی بر دیگری را بر اساس توابع ریاضی مشخص کند، که این امر دقت مدل‌سازی را در محیط‌های واقعی به شدت افزایش می‌دهد.

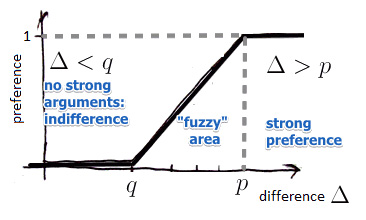
در دنیای تصمیم‌گیری چندمعیاره (MCDM)، روش پرومتی به دلیل انعطاف‌پذیری در تعریف انواع مختلف توابع ترجیح (مانند تابعی، پله‌ای یا خطی) شناخته می‌شود. این ویژگی به تصمیم‌گیرنده اجازه می‌دهد تا آستانه‌های بی‌تفاوتی و ترجیح را با دقت بسیار بالایی وارد مدل کند. به همین دلیل، در پروژه‌هایی که نظرات خبرگان دارای جزئیات ظریف است، پرومتی از روش‌هایی مثل روش TOPSIS یا روش SAW پیشی می‌گیرد و خروجی‌های واقعی‌تری ارائه می‌دهد.

استفاده از این متد در حوزه تحقیق در عملیات نیازمند درک عمیق از جریان‌های مطلوبیت است. ما در سایت فرابگیر، این روش را به عنوان یک تکنیک استراتژیک برای مسائل حساس مانند انتخاب تکنولوژی، مکان‌یابی صنعتی و مدیریت منابع انسانی پیشنهاد می‌کنیم. پرومتی با ارائه دو نسخه اصلی (نسخه I برای رتبه‌بندی جزئی و نسخه II برای رتبه‌بندی کامل)، ابزاری همه‌جانبه برای متخصصان آموزش مدیریت فراهم می‌آورد تا پیچیده‌ترین سناریوها را تحلیل کنند.

آنچه می خوانید

مقدمه و تبارشناسی روش پرومتی

روش PROMETHEE (PROMETHEE) به عنوان یکی از روش‌های نوین و کارآمد در تصمیم‌گیری چندمعیاره (MCDM) شناخته می‌شود. این روش که در دهه 1980 توسط دو محقق بلژیکی به نام‌های “ژان پیر برنز” و “برتراند مارسکال” ارائه شد، بر پایه نظریه ترجیح بنا شده و با هدف ساده‌سازی و شفاف‌سازی فرآیند تصمیم‌گیری توسعه یافته است.

تصمیم‌گیری در دنیای پیچیده امروزی، همواره با چالش‌های متعددی همراه بوده است. انتخاب بهترین گزینه از بین چندین گزینه با معیارهای مختلف، یکی از این چالش‌ها است. در این میان، روش‌های گوناگونی برای حل این مسأله وجود دارد که روش PROMETHEE (PROMETHEE) به عنوان یکی از روش‌های نوین و کارآمد در تصمیم‌گیری چندمعیاره (MCDM) شناخته می‌شود.

پیشینه روش PROMETHEE: ریشه در نظریه ترجیح

دهه 1970: نقطه عطفی در تاریخ MCDM

دهه 1970 را می‌توان به عنوان نقطه عطفی در تاریخ MCDM دانست. در این دهه، شاهد ظهور روش‌های جدیدی برای حل مسائل چندمعیاره بودیم که روش‌های مبتنی بر ترجیح، جایگاه ویژه‌ای در میان آنها داشتند.

نظریه ترجیح: مبنای روش‌های نوین MCDM

نظریه ترجیح، به بررسی چگونگی انتخاب افراد بین گزینه‌های مختلف می‌پردازد. این نظریه بیان می‌کند که افراد در انتخاب خود، به ترجیحات و اولویت‌هایشان توجه می‌کنند.

روش‌های مبتنی بر ترجیح: گامی فراتر از روش‌های سنتی

روش‌های سنتی MCDM مانند روش مجموع وزنی، تنها به معیارها و امتیاز آنها توجه می‌کنند و ترجیحات تصمیم‌گیرنده را در نظر نمی‌گیرند. در مقابل، روش‌های مبتنی بر ترجیح، با در نظر گرفتن ترجیحات و اولویت‌های تصمیم‌گیرنده، به انتخابی دقیق‌تر و متناسب با نیازهای او کمک می‌کنند.

تولد روش PROMETHEE: فرزند نظریه ترجیح

روش PROMETHEE به عنوان یکی از روش‌های مبتنی بر ترجیح، در سال 1982 توسط دو محقق بلژیکی به نام‌های “ژان پیر برنز” و “برتراند مارسکال” معرفی شد. این روش که بر پایه نظریه ترجیح بنا شده است، به دنبال ساده‌سازی و شفاف‌سازی فرآیند تصمیم‌گیری چندمعیاره است.

مزایای روش PROMETHEE

قابلیت انعطاف‌پذیری: روش PROMETHEE برای حل مسائل مختلف با معیارهای متنوع و گاه متضاد، قابل استفاده است.
توانایی در نظر گرفتن ترجیحات تصمیم‌گیرنده: این روش با در نظر گرفتن ترجیحات و نظرات شما در فرآیند تصمیم‌گیری، انتخابی ایده‌آل و متناسب با نیازهایتان را به ارمغان می‌آورد.
ارائه اطلاعات دقیق: روش PROMETHEE با ارائه اطلاعات دقیق در مورد برتری و ترجیح گزینه‌ها، به شما در انتخابی مطمئن و با آگاهی کامل کمک می‌کند.
سادگی و شفافیت: روش PROMETHEE به زبان ساده قابل فهم و اجرا است.

معایب روش PROMETHEE

محاسبات پیچیده: در برخی از موارد، محاسبات مربوط به روش PROMETHEE می‌تواند پیچیده باشد.
نیاز به اطلاعات: برای استفاده از روش PROMETHEE به اطلاعات کامل و دقیقی در مورد معیارها و گزینه‌ها نیاز است.

کاربردهای روش PROMETHEE

روش PROMETHEE به عنوان یک روش قدرتمند در تصمیم‌گیری چندمعیاره، در زمینه‌های مختلفی کاربرد دارد. برخی از کاربردهای این روش عبارتند از:

انتخاب:

بهترین تامین‌کننده: با توجه به معیارهایی مانند قیمت، کیفیت، زمان تحویل و …
بهترین پروژه: با توجه به معیارهایی مانند سودآوری، ریسک، زمان انجام و …
بهترین محل: برای احداث یک کارخانه، با توجه به معیارهایی مانند دسترسی به مواد اولیه، نیروی کار، بازار و …
بهترین شغل: با توجه به معیارهایی مانند حقوق، مزایا، فرصت‌های پیشرفت، علاقه و …
بهترین رشته تحصیلی: با توجه به معیارهایی مانند علاقه، بازار کار، رتبه دانشگاه و …

رتبه‌بندی:

دانشگاه‌ها: با توجه به معیارهایی مانند کیفیت آموزشی، امکانات رفاهی، رتبه علمی و …
بیمارستان‌ها: با توجه به معیارهایی مانند کیفیت خدمات، تخصص پزشکان، هزینه و …
محصولات: با توجه به معیارهایی مانند قیمت، کیفیت، کارایی، برند و …
پروژه‌های تحقیقاتی: با توجه به معیارهایی مانند نوآوری، اهمیت، امکان‌پذیری و …

انتخاب و رتبه‌بندی در:

بانکداری: انتخاب بهترین طرح تسهیلات
بیمه: انتخاب بهترین نوع بیمه
بازاریابی: انتخاب بهترین استراتژی بازاریابی
تولید: انتخاب بهترین روش تولید
منابع انسانی: انتخاب بهترین روش استخدام

انواع روش های پرومته: تنوعی برای انتخابی دقیق

روش PROMETHEE در دو نوع اصلی ارائه شده است که هر کدام مزایا و معایب خاص خود را دارند:

1. روش PROMETHEE 1:

مبتنی بر ماتریس ترجیحات: این روش از ماتریس ترجیحات برای رتبه‌بندی گزینه‌ها استفاده می‌کند.
سادگی و سهولت استفاده: روش PROMETHEE 1 به دلیل سادگی و سهولت استفاده، برای حل مسائل ساده‌تر مناسب است.
محاسبات کم: این روش به محاسبات کمتری نسبت به روش PROMETHEE 2 نیاز دارد.

2. روش PROMETHEE 2:

مبتنی بر ماتریس جریان ورودی و خروجی: این روش از ماتریس جریان ورودی و خروجی برای رتبه‌بندی گزینه‌ها استفاده می‌کند.
اطلاعات دقیق‌تر: روش PROMETHEE 2 اطلاعات دقیق‌تری در مورد برتری و ترجیح گزینه‌ها ارائه می‌دهد.
قابلیت در نظر گرفتن ترجیحات غیرخطی: این روش قادر به در نظر گرفتن ترجیحات غیرخطی تصمیم‌گیرنده است.
محاسبات پیچیده‌تر: روش PROMETHEE 2 به محاسبات پیچیده‌تری نسبت به روش PROMETHEE 1 نیاز دارد.

انتخاب روش مناسب:

انتخاب روش مناسب از بین دو روش PROMETHEE 1 و 2 به عوامل مختلفی مانند ماهیت مسأله، ترجیحات تصمیم‌گیرنده و در دسترس بودن اطلاعات بستگی دارد. علاوه بر دو روش اصلی، روش‌های دیگری نیز از خانواده پرومته وجود دارند که عبارتند از:

پرومته 3: برای تحلیل روابط ترجیح و غیرترجیح
پرومته 4: برای حل مسائل با تعداد گزینه‌های نامحدود
پرومته 5: برای حل مسائل با محدودیت
پرومته 6: برای شبیه‌سازی مغز انسان در تصمیم‌گیری

گام های روش PROMETHEE

1. تعریف معیارها:

در این گام، معیارهای مؤثر در تصمیم‌گیری مشخص می‌شوند. معیارها می‌توانند کیفی یا کمی باشند.

2. تعیین وزن معیارها:

در این گام، اهمیت هر معیار با توجه به نظر تصمیم‌گیرنده تعیین می‌شود. برای تعیین وزن معیارها می‌توان از روش‌های مختلفی مانند روش AHP، روش دلفی و … استفاده کرد.

3. محاسبه ماتریس ترجیحات:

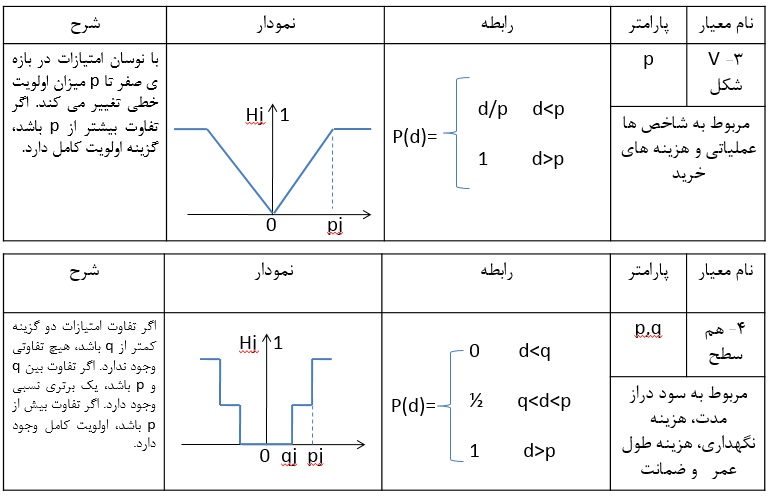
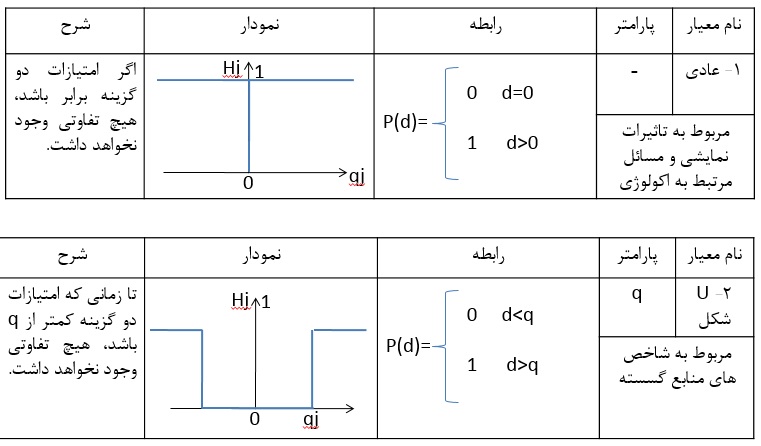
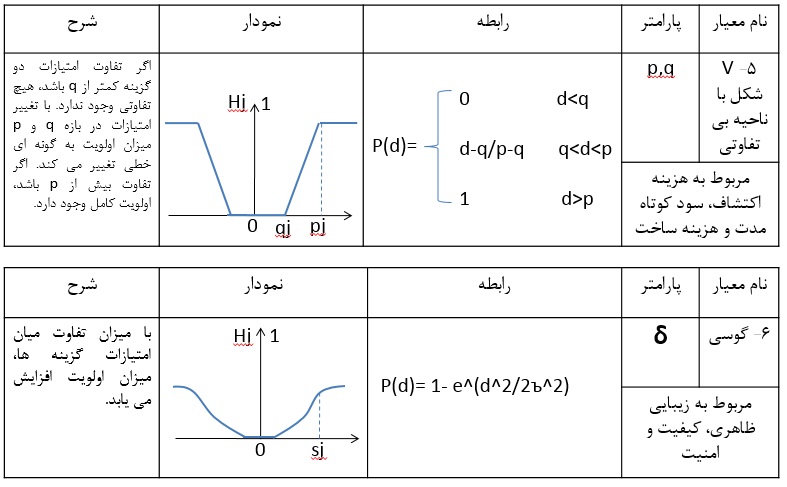
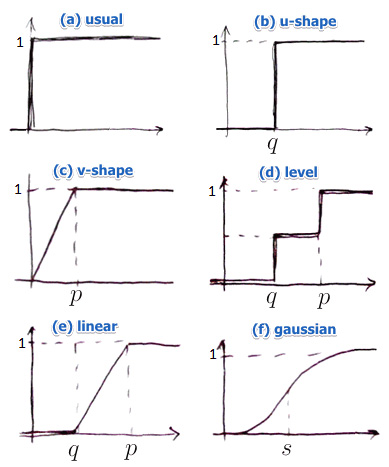
در این گام، ترجیح هر گزینه نسبت به سایر گزینه‌ها برای هر معیار محاسبه می‌شود. برای محاسبه ماتریس ترجیحات می‌توان از روش‌های مختلفی مانند روش تابع عادی، روش U شکل و … استفاده کرد.

4. محاسبه موزون برتری

مجموع موزون برتری گزینه a نسبت به b كه آن را با (π(a,b نشان می دهند.

π(a,b) = Σ P_j(a,b)W_j

π(b,a) = Σ P_j(b,a)W_j

5. محاسبه جریان ورودی و خروجی

جریان ورودی و جریان خروجی در این گام صورت می پذیرد:

جریان خروجی: بیان می کند یک گزینه مانند a چه قدر از گزینه های دیگر برتر است. هرچه این مقدار بیشتر باشد این گزینه برتر خواهد بود.

Φ⁺(a) = Σ π(a,x)

جریان ورودی: بیان می کند که گزینه های دیگر چه قدر برگزینه a برتر می باشند. هرچه این مقدار کمتر باشد این گزینه بهتر خواهد بود.

Φ^–(a) = Σ π(x,a)

6. رتبه‌بندی نهایی

رتبه بندی ها از مقایسه جریان های برتری مثبت و منفی به دست می آیند. که p و I و R به ترتیب نشان دهنده ارجحیت،بی تفاوتی و غیر قابل مقایسه بودن است.

رابطه a p^I b نشان می دهد برتری a ناشی از ضعف b است.
وقتی که a I^I b ، جریان های مثبت و منفی با هم برابرند.
وقتی a R^I b قدرت بیشتر یک گزینه ناشی ازضعف گزینه دیگر است.در چنین حالتی اطلاعاتی که توسط دو جریان به وجود می آیند سازگار نیستند.

به دلیل پیچیدگی بالای مقایسات زوجی در این روش، استفاده از فایل اکسل روش PROMETHEE در آکادمی نرم‌افزار فرابگیر، برای محققان بسیار حیاتی است تا از صحت محاسبات اطمینان یابند.

مثال روش promethee

فردی قصد دارد كه یكی از 4 مدل گوشی همراه سامسونگ، ال جی، سونی، اپل را خریداری كند. برای این گوشی ها 4 شاخص در نظر گرفته شده است. با روش پرومته این رتبه بندی را انجام می دهیم.

اوزان	0.35	0.25	0.25	0.15
نوع	منفی	مثبت	مثبت	مثبت
گزینه ها	قیمت	حافظه	دوربین	زیبایی
M1	250	16	12	5
M2	200	16	8	3
M3	300	32	16	4
M4	275	32	8	2

ماتریس تصمیم گیری

گام اول: نرمال سازی ماتریس

برای از بین بردن اثر علامت شاخص ها ابتدا ماتریس را نرمال می کنیم. می توانیم از انواع روش های نرمال سازی نرم، اقلیدسی و غیره برای این منظور استفاده کنیم.

ماتریس تصمیم گیری نرمال
گزینه ها	قیمت	حافظه	دوربین	زیبایی
M1	0.50	0.00	0.50	1.00
M2	1.00	0.00	0.00	0.33
M3	0.00	1.00	1.00	0.67
M4	0.25	1.00	0.00	0.00

ماتریس نرمال شده

گام دوم: محاسبه اختلاف بین گزینه ها

در این گام اختلاف هر یک از گزینه ها را با همدیگر محاسبه می کنیم.

گزینه ها	قیمت	حافظه	دوربین	زیبایی
M1-M2	-0.50	0.00	0.50	0.67
M1-M3	0.50	-1.00	-0.50	0.33
M1-M4	0.25	-1.00	0.50	1.00
M2-M1	0.50	0.00	-0.50	-0.67
M2-M3	1.00	-1.00	-1.00	-0.33
M2-M4	0.75	-1.00	0.00	0.33
M3-M1	-0.50	1.00	0.50	-0.33
M3-M2	-1.00	1.00	1.00	0.33
M3-M4	-0.25	0.00	1.00	0.67
M4-M1	-0.25	1.00	-0.50	-1.00
M4-M2	-0.75	1.00	0.00	-0.33
M4-M3	0.25	0.00	-1.00	-0.67

ماتریس اختلاف بین گزینه ها

گام سوم: محاسبه ترجحات بین گزینه

برای محاسبه ترجیحات، از انواع تابع ترجیح می توان استفاده کرد. در این مثال از تابع ترجیح عادی استفاده شده است.

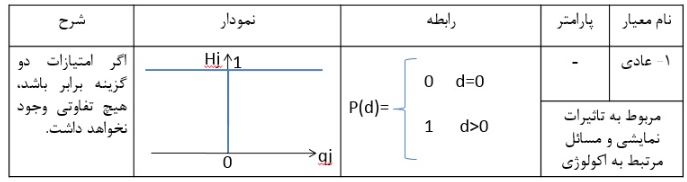
بدین معنی که گزینه هایی که اختلاف آنها کمتر یا مساوی صفر باشد مقدار صفر و سایر گزینه ها مقدار اختلاف را به خود اختصاص می دهند.

اوزان	0.35	0.25	0.25	0.15
گزینه ها	قیمت	حافظه	دوربین	زیبایی
M1-M2	0.00	0.00	0.50	0.67
M1-M3	0.50	0.00	0.00	0.33
M1-M4	0.25	0.00	0.50	1.00
M2-M1	0.50	0.00	0.00	0.00
M2-M3	1.00	0.00	0.00	0.00
M2-M4	0.75	0.00	0.00	0.33
M3-M1	0.00	1.00	0.50	0.00
M3-M2	0.00	1.00	1.00	0.33
M3-M4	0.00	0.00	1.00	0.67
M4-M1	0.00	1.00	0.00	0.00
M4-M2	0.00	1.00	0.00	0.00
M4-M3	0.25	0.00	0.00	0.00

ماتریس ترجیحات

گام چهارم: محاسبه ماتریس ترجیح وزن دار

در این گام اوزان هر یک از معیارها در مقدار ترجیح آن ضرب و ماتریس ترجیح وزن دار محاسبه می شود. در ادامه مقدار ترجیح وزن دار هر یک از اختلافات با هم جمع می شود

گزینه ها	قیمت	حافظه	دوربین	زیبایی	SUM
M1-M2	0.000	0.000	0.125	0.100	0.2250
M1-M3	0.175	0.000	0.000	0.050	0.2250
M1-M4	0.088	0.000	0.125	0.150	0.3625
M2-M1	0.175	0.000	0.000	0.000	0.1750
M2-M3	0.350	0.000	0.000	0.000	0.3500
M2-M4	0.263	0.000	0.000	0.050	0.3125
M3-M1	0.000	0.250	0.125	0.000	0.3750
M3-M2	0.000	0.250	0.250	0.050	0.5500
M3-M4	0.000	0.000	0.250	0.100	0.3500
M4-M1	0.000	0.250	0.000	0.000	0.2500
M4-M2	0.000	0.250	0.000	0.000	0.2500
M4-M3	0.088	0.000	0.000	0.000	0.0875

ماتریس ترجیح وزن دار

در ادامه با توجه به مجموع وزن های بدست آمده ماتریس ارتباط بین گزینه ها تشکیل می شود.

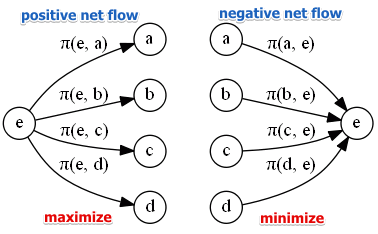
گزینه ها	M1	M2	M3	M4	ф+
M1	0.00	0.23	0.23	0.36	0.8125
M2	0.18	0.00	0.35	0.31	0.8375
M3	0.38	0.55	0.00	0.35	1.2750
M4	0.25	0.25	0.09	0.00	0.5875
ф-	0.8000	1.0250	0.6625	1.0250

ماتریس ارتباط بین گزینه ها

گام پنجم: رتبه بندی گزینه ها

برای رتبه بندی گزینه ها از قاعده اصلی مقایسه جریان های ورودی و خروجی استفاده می کنیم.

M1>M2	R
M3>M1	P
M1>M4	R
M3>M2	P
M2>M4	P
M3>M4	R

مقایسه گزینه ها

با مقایسه نتایج می بینم که گزینه سوم بر گزینه دوم و اول ارحج است. گزینه دوم به گزینه چهارم ارحج است. بین گزینه اول و دوم، و اول و چهارم نمی توانیم تصمیم گیری انجام دهیم.

اکسل روش promethee به همراه فیلم آموزشی

تفاوت PROMETHEE I و PROMETHEE II

یکی از ویژگی‌های منحصر به فرد این روش، امکان ارائه رتبه‌بندی ناقص است. در PROMETHEE I، ممکن است دو گزینه غیرقابل مقایسه تشخیص داده شوند (زمانی که یکی در جریان خروجی بهتر و دیگری در جریان ورودی بدتر باشد). اما در PROMETHEE II، با استفاده از جریان خالص، یک رتبه‌بندی کامل و قطعی ارائه می‌شود. این تفکیک به تحلیل‌گران در رتبه‌بندی گزینه‌ها کمک می‌کند تا نقاط ابهام در تصمیم‌گیری را شناسایی کنند.

سوالات متداول

تابع ترجیح در روش پرومتی بر چه اساسی انتخاب می‌شود؟

بر اساس ماهیت معیار و نظر خبره؛ مثلاً برای معیارهای عددی پیوسته معمولاً از تابع V-shape یا Linear با آستانه ترجیح استفاده می‌شود.

آیا پرومتی از روش VIKOR دقیق‌تر است؟

پرومتی به دلیل استفاده از توابع ترجیح متنوع، انعطاف بیشتری در مدل‌سازی ذهنیات تصمیم‌گیرنده دارد، در حالی که روش VIKOR بیشتر بر تعامل بین سودمندی اکثریت و مخالفت اقلیت تمرکز دارد.

خروجی نهایی پرومتی چیست؟

خروجی نهایی عددی بین ۱- و ۱+ (جریان خالص) است که هرچه بزرگتر باشد، گزینه مطلوب‌تر است.

نتیجه‌گیری و جمع‌بندی نهایی

روش PROMETHEE به عنوان یکی از پیشرفته‌ترین ابزارهای رتبه‌بندی گزینه‌ها، با عبور از محدودیت‌های روش‌های سنتی، استانداردی نوین در مدل‌سازی ترجیحات انسانی ایجاد کرده است. قدرت اصلی این روش در استفاده از توابع ترجیح و آستانه‌های بی‌تفاوتی نهفته است که اجازه می‌دهد تفاوت‌های کوچک بین گزینه‌ها به شکلی واقع‌گرایانه در خروجی نهایی اثر بگذارند. این رویکرد در مباحث تحقیق در عملیات، پرومتی را به انتخابی بی‌بدیل برای مسائلی تبدیل کرده است که در آن‌ها دقت مدل‌سازی بر سادگی محاسبات اولویت دارد.

پیاده‌سازی موفق این روش در پروژه‌های پژوهشی، نیازمند تسلط بر مفاهیم جریان‌های ورودی و خروجی و تحلیل روابط برتری است. محققان با ارائه رتبه‌بندی‌های حاصل از پرومتی در بخش آمار و تحلیل داده، سطح علمی کار خود را به استانداردهای مقالات تراز اول دنیا نزدیک می‌کنند. ترکیب این متد با روش‌های وزن‌دهی قدرتمند مانند روش BWM، زنجیره‌ای از تصمیم‌گیری مستدل و منطقی را ایجاد می‌کند که قدرت دفاع از نتایج را در هر مجمع علمی و مدیریتی تضمین می‌نماید.

در نهایت، برای غلبه بر پیچیدگی‌های عددی این روش، بهره‌گیری از ابزارهای تخصصی در آکادمی نرم‌افزار فرابگیر یک راهکار هوشمندانه است. استفاده از فایل‌های محاسباتی استاندارد، نه تنها سرعت اجرای پروژه را افزایش می‌دهد، بلکه امکان تمرکز بر تحلیل‌های حساسیت و تفسیر نمودارهای GAIA (که بخش بصری پرومتی است) را فراهم می‌آورد. ما بر این باوریم که یادگیری روش پرومتی، گامی بزرگ برای هر متخصص حوزه تصمیم‌گیری چندمعیاره (MCDM) است تا بتواند در دنیای پر از متغیرهای متضاد، بهترین و پایدارترین انتخاب را رقم بزند.

نمایش: 32