آموزش جامع روش ELECTRE
روش ELECTRE که مخفف ELimination Et Choix Traduisant la REalité است، در اواخر دهه ۶۰ میلادی در فرانسه ابداع شد تا با نگاهی واقعبینانهتر به حذف گزینههای نامناسب بپردازد. این روش برخلاف متدهایی که با یک عدد نهایی گزینهها را رتبهبندی میکنند (مانند روش SAW)، بر پایه مفهوم «رابطه برتری» (Outranking Relation) استوار است. منطق الکتره بر این است که یک گزینه بر گزینه دیگر برتری دارد، اگر و تنها اگر شواهد کافی برای برتری آن وجود داشته باشد و شواهد مخالف (ناهماهنگی) شدیدی علیه آن وجود نداشته باشد.
در دنیای تصمیمگیری چندمعیاره (MCDM)، روش ELECTRE (الکتره) به عنوان ابزاری برای غربالگری و رتبهبندی گزینهها در محیطهایی با معیارهای متضاد شناخته میشود. این روش با استفاده از آستانههای پذیرش، اجازه میدهد تا گزینههایی که در برخی معیارها بسیار ضعیف هستند، حتی اگر در مجموع امتیاز خوبی داشته باشند، حذف یا به رتبههای پایینتر منتقل شوند. این ویژگی، روش ELECTRE (الکتره) را از روشهایی مثل روش TOPSIS متمایز کرده و آن را به گزینهای ایدهآل برای مسائل حساس مهندسی و محیط زیست تبدیل کرده است.
استفاده از نسخههای مختلف این روش (مانند ELECTRE I, II, III, IV) در حوزه تحقیق در عملیات نیازمند دقت بالا در تشکیل ماتریسهای مقایسات زوجی است. ما در سایت فرابگیر، آموزش این متد را به عنوان یک مهارت ضروری برای متخصصان آموزش مدیریت ارائه میدهیم تا بتوانند فرآیند انتخاب را از یک جمع ساده امتیازات به یک تحلیل عمیق از روابط تسلط تبدیل کنند. روش ELECTRE (الکتره) با حذف گزینههای “تحت سلطه”، مسیر را برای اتخاذ تصمیم نهایی با بالاترین درجه اطمینان هموار میسازد.
آنچه می خوانید
جایگاه روش ELECTRE الکتره در تصمیمگیری
تاریخچه روش روش ELECTRE (الکتره) به اروپا در اواسط دهه 1960 میلادی بر می گردد و می توان به عنوان یکی از بهترین روش های در نظر گرفته شده در حل مسائل تصمیم گیری با معیارهای چندگانه برشمرد. برنارد روی به عنوان پدر روش الکتره شناخته می شود.
این روش برای اولین بار توسط برنارد روی و همکارانش در شرکت مشاوره سما پیشنهاد گردید. این شرکت تیمی را تشکیل داد تا در مورد مسائل چند معیاره، برای تصمیم گیری در مورد فعالیت های جدید شرکت به تخقیق بپردازند که در اصل این روش جزو یکی از اولین رویکردهای تصمیم گیری بود.
در این روش، وقتی تصمیم گیرنده با بیشتر از 5 معیار در بررسی گزینه هایش روبه رو باشد نتیجه دارایی کارایی مناسبی می باشد. اگر تا 12 الی 13 معیار باشد هنوز کارایی خود را حفظ می کند. در مقایسات زوجی درجه توافق از اوزان به صورت Wj و مقادیر ارزیابی وزین به صورت ماتریس Vij می باشد.
کلیه این مراحل بر مبنای یک مجموعه هماهنگ و یک مجموعه ناهماهنگ پایه ریزی می شوند . به دلیل این موضوع این روش به آنالیز همگانی هم معروف می باشد. برای استفاده از این روش فرضیاتی مورد نیاز است که عبارتند از:
- معیارهای باید کمی یا قابل تبدیل به صورت کمی باشند.
- معیارها باید به طور کامل ناهمگن باشند.
در اصل هدف روش روش ELECTRE (الکتره) جداکردن گزینه هایی است که در ارزیابی بر اساس بیشتر معیارها ترجیح داده می شوند.
نقاط ضعف و قوت روش ELECTRE الکتره
- یکی از نقاط ضعف روش الکتری استفاده از حداقل آستانه C و D برای محاسبه ماتریس هماهنگی و ناهماهنگی موثرمی باشد.
- زیرا با توجه به این که D وC به نسبت دلخواه بوده و همچنین می توانند روی جواب نهایی تا حد زیادی تاثیرگذار باشند، بنابراین تغییر در میزان حد آستانه جواب های مساله را تا حدود زیادی دستخوش تغییر می نماید.
- از طرفی، این روش، رتبه بندی کامل و نهایی را به ما نمی دهد و به ارایه گزینه های برتر اکتفا می کند.
- از مزایای آن می توان به قوانین ساده، حداکثر استفاده از اطلاعات ماتریس تصمیم و در نهایت محاسبات منظم و منسجم آن اشاده نمود.
مراحل روش ELECTRE الکتره
مراحل الگوریتم حل مسایل تصمیم از طریق روش ELECTRE (الکتره) را می توان به صورت زیر تشریح کرد:
1- از بین بردن تفاوت مقیاسی داده های تصمیم گیری با استفاده از نرم اقلیدسی ( ماتریس نرمال R):
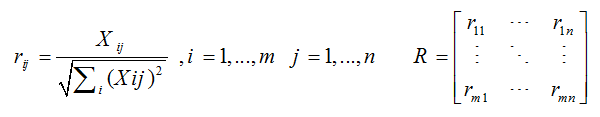
2- اعمال اوزان معیارها و تشکیل ماتریس وزین V با استفاده از بردار معلوم W :
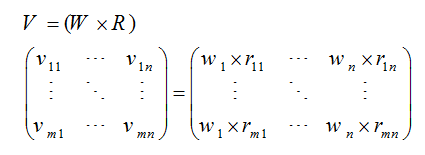
3- تعیین مجموعه هماهنگی و ناهماهنگی برای هر زوج از گزینه های k,l:
(k, l = 1,2,3…, m ; l≠k)
مجموعه شاخص های موجود {J={j|j = 1,2,…,n را به دو زیرمجموعه متمایز هماهنگ (Ckj) و ناهماهنگ (Dkl) تقسیم می کنیم. به طوری که اگر شاخص مورد نظر دارای جنبه مثبت باشد، داریم:
CKI = {j€ J | Xkj ≥ Xlj}
مجموعه هماهنگ (Ckl) از مقایسه گزینه های Al و Ak که در آن در صورت مثبت بودن جنبه معیار، Ak از Al بیشتر بوده و در صورت منفی بودن جنبه معیار ( مانند هزینه) Ak از Al کمتر باشد، تشکیل می شود. بنابراین اگر شاخص، دارای جنبه منفی باشد، داریم:
CKI = {j€ J | Xkj ≤ Xlj}
و برعکس زیرمجموعه مکمل به نام مجموعه ناهماهنگ (Dkl) مجموعه ای از شاخص هاست که به ازای آنها برای معیارها با جنبه مثبت داشته باشیم:
D KI = {j€ J | Xkj ≤ Xlj} = J – CKI
4- محاسبه ماتریس هماهنگی
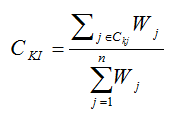
برای ساخت ماتریس هماهنگی، معیار هماهنگی برابر با مجموع اوزان (wj) شاخص هایی است که مجموعه CKI را تشکیل می دهند. بدین صورت معیار هماهنگی (Ckl) بین Al و Ak بدین قرار است:
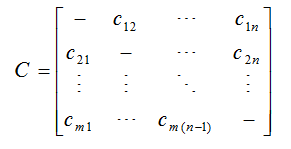
معیار هماهنگی (Ckl) منعکس کننده برتری Ak در مقایسه با Al است به طوری که l 0≤Clk≤1 l خواهد بود. هرچه مقدار به 1 نزدیک باشد، به ارجحیت بیشتر گزینه k نسبت به گزینه I اشاره دارد.
بنابراین در ادامه می بینیم مقادیر مختلف معیارهای (Ckl (k, l=1,2,…;m, k≠l ماتریس هماهنگی C را که به طور طبیعی نامتقارن خواهد بود، تشکیل می دهند.
5- محاسبه ماتریس ناهماهنگی
معیار ناهماهنگی مجموعه DKI برعکس معیار CKI نشان دهنده شدت عدم ترجیح Ak در مقایسه با Al می باشد. در اصل در این قدم، بعد از مشخص کردن مجموعه ناهماهنگی برای تمام جفت گزینه ها ( هم برای DKI و هم برای DIK)، برای محاسبه معیار ناهماهنگی، مقدار بیشینه « اختلافات دو گزینه» در معیارهای مجموعه ناهماهنگی بر مقدار بیشینه « اختلاف گزینه» در کل معیارهای موجود تقسیم می نماییم. فرمول زیر مفهوم بالا را به صورت واضح تری نشان می دهد.
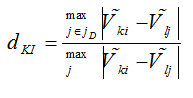
لذا در ادامه می توانیم بر اساس رابطه ریاضی بالا، ماتریس ناهماهنگی D را تشکیل دهیم.
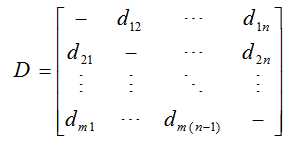
6-مشخص نمودن ماتریس هماهنگ موثر
حال بازهم برای اینکه یک بررسی نسبی بهتری در رابطه با ارجحیت گزینه ها نسبت به هم را داشته باشیم، مولفه های ماتریس هماهنگی را با یک مقدار حد آستانه مقایسه می کنیم تا ببینیم کدام یک از این مولفه ها از این آستانه هماهنگی C2 بیشتر می باشندو حداقل انتظارات ما را برآورده می سازند. C را می توان به صورت متوسط از معیارهای هماهنگی بدست آورد.
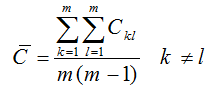
در ادامه بعد از مقایسه تمام مولفه ها با مقدار حداقل آستانه، ماتریس بولین h که یک ماتریس با مولفه های 0 و 1 می باشد را تشکیل می دهیم. قاعده اختصاص به 0 و 1 به ازای هر کدام از مولفه ها به صورت زیر می باشد.
HKI=1 اگر CKI ≥ Ĉ
HKI=0 اگر CKI < Ĉ
بنابراین به راحتی می توانیم تشخیص دهیم هر مولفه ای در ماتریس H ( ماتریس هماهنگ موثر) که دارای مقدار 1 باشد، نشان دهنده یک گزینه موثر و به طور محسوس مسلط بر دیگری است.
7- مشخص نمودن ماتریس ناهماهنگ موثر
حال به همان صورت که مقدار ماتریس هماهنگی موثر رابرای مولفه های ماتریس هماهنگی محاسبه کردیم، این روش را یرای مثادیر ماتریس ناهماهنگی جهت محاسبه ماتریس ناهماهنگی موثر نیز پیاده می کنیم. بنابراین برای تشکیل ماتریس ناهماهنگی موثر، باید مقدار حداقل آستانه را که سطح ناهماهنگی نیز نامیده می شود، محاسبه و مولفه های ماتریس را با آن مقدار آستانه مقایسه کنیم.
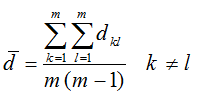
حال ماتریس ناهماهنگی موثر را که ماتریس بولین G نام گذاری می کنیم ، با رعایت قاعده زیر تشکیل می دهیم.
gKI=0 اگر dKI ≥ ḏ
gKI=1 اگر dKI < ḏ
نتیجه حال از این مرحله، یک ماتریس با مولفه های 0 و1 می باشه که مقادیر 1 در این مولفه، نشان دهنده تسلیم بود مسلم گزینه k درمقابل گزینه I می باشد.
8- مشخص نمودن ماتریس کلی و موثر
حال برای اینکه در نهایت بتوانیم یک نتیجه گیری از برتری گزینه ها باهم را داشته باشیم، دو ماترس هماهنگی موثر و ناهماهنگی موثر را در هم ضرب می کنیم. این ماتریس در صورتی دارای مولفه 1 است که وقتی ضرب ماتریسی در آن انجام می شود، هر دو مولفه متناظری که در هم ضرب می شوند 1 باشند. برای دو گزینه k و l زمانی ekl=1 رخ میدهد که k نسبت به I دارای برتری قابل قبول در ماتریس hKI و I نسبت به k تسلیم کامل در ماتریس gkl باشد.
eKI = hKI . gKI
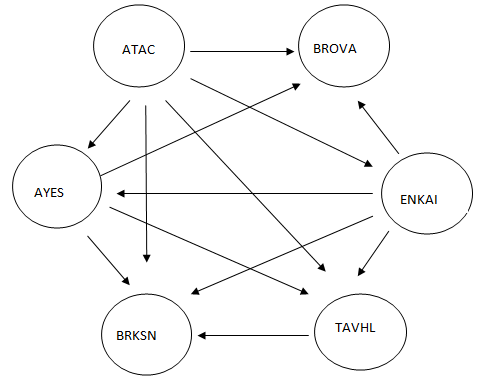
9- رسم شبکه ترجیح
حال باید به تعداد گزینه های مساله ای که با آن مواجه هستیم گره رسم کنیم. برای رسم کمان بین این گره ها، اگر در ماتریس E بین دو گزینه مولفه 1 وجود داشت، از گره سطر مربوطه در ماتریس به گره ستون مربوطه در ماتریس یک فلش جهت دار رسم می کنیم. هر کدام که بیشترین خروجی را داشته باشند، از ترجیح و برتری بیشتری برخوردار است.
به دلیل حجم عظیم مقایسات زوجی (n*(n-1) مقایسه)، استفاده از ابزارهای محاسباتی در آکادمی نرمافزار فرابگیر برای جلوگیری از اشتباهات انسانی توصیه میشود.
مثال روش ELECTRE الکتره
یک کشور قصد خرید هواپیما جنگنده ای را برای تکمیل ارتش خود دارد. کارشناسان برای انتخاب جنگنده مطلوب خود با معیارهای مانور، میزان ثبت ( اطمینان)، هزینه، شتاب، ظرفیت و سرعت مواجه هستند که ماتریس اطلاعات مربوطه به صورت زیر می باشد. این کارشناسان را با استفاده از روش روش ELECTRE (الکتره) راهنمایی نمایید.
| ماتریس تصمیم گیری | ||||||
| علامت | + | + | + | – | + | + |
| سرعت | ظرفیت | شتاب | هزینه | اطمینان | مانور | |
| A1 | 2 | 1.5 | 2 | 5.5 | 5 | 9 |
| A2 | 2.5 | 2.7 | 1.8 | 6.5 | 3 | 5 |
| A3 | 1.8 | 2 | 2.1 | 4.5 | 7 | 7 |
| A4 | 2.2 | 1.8 | 2 | 5 | 5 | 5 |
| اوزان | 0.2 | 0.1 | 0.1 | 0.1 | 0.2 | 0.3 |
همان طور که مشاهده می شود به غیر از هزینه که دارای جنبه منفی می باشد، بقیه شاخص ها دارای جنبه مثبت می باشند و هرچه بیشتر باشند از ترجیح بیشتری برخوردار هستند.
گام اول: ماتریس را براساس روش ارائه شده بی مقیاس می کنیم.
| بی مقیاس سازی | ||||||
| علامت | + | + | + | – | + | + |
| سرعت | ظرفیت | شتاب | هزینه | اطمینان | مانور | |
| A1 | 0.467 | 0.366 | 0.506 | 0.507 | 0.481 | 0.671 |
| A2 | 0.584 | 0.659 | 0.455 | 0.599 | 0.289 | 0.373 |
| A3 | 0.420 | 0.488 | 0.531 | 0.415 | 0.674 | 0.522 |
| A4 | 0.514 | 0.439 | 0.506 | 0.461 | 0.481 | 0.373 |
| اوزان | 0.2 | 0.1 | 0.1 | 0.1 | 0.2 | 0.3 |
گام دوم: حال در این مرحله با اعمال اوزان، ماتریس وزین V را تشکیل می دهیم.
| ضرب در اوزان و ماتریس وزین | ||||||
| علامت | + | + | + | – | + | + |
| سرعت | ظرفیت | شتاب | هزینه | اطمینان | مانور | |
| A1 | 0.093 | 0.037 | 0.051 | 0.051 | 0.096 | 0.201 |
| A2 | 0.117 | 0.066 | 0.046 | 0.060 | 0.058 | 0.112 |
| A3 | 0.084 | 0.049 | 0.053 | 0.041 | 0.135 | 0.157 |
| A4 | 0.103 | 0.044 | 0.051 | 0.046 | 0.096 | 0.112 |
گام سوم: ماتریس هماهنگی را بر اساس روش ذکر شده محاسبه می کنیم.
نکته: یادآوری می کنیم که شاخص هزینه منفی است لذا در حالت مقایسه خلاف سایر شاخص ها اعمال می گردد.
به طور مثال دو گزینه A1,A2 را با هم مقایسه می کنیم:
- آیا 0.093 > 0.117 ؟ آیا 0.037 > 0.066 ؟ آیا 0.051 > 0.046 ؟ این شاخص منفی است و برعکس: آیا 0.051 < 0.060 ؟ آیا 0.096 > 0.058 ؟ آیا 0.201 > 0.112 ؟
- پس از مقایسه این شروط فقط برای شاخص شتاب، هزینه، اطمینان و مانور برقرار است و برای سایر شاخص ها “-” قرار می گیرد. لذا {C12={3,4,5,6 خواهد بود.
- حال در جدول به جای هر گزینه وزن آن را می نویسیم. به طور مثال اوزان { C12 = {0.1 , 0.1 , 0.2 , 0.3 و مجموع آن 0.7 خواهد شد. به همین ترتیب جدول هماهنگی را به صورت زیر تشکیل می دهیم.
| مقاسیه هماهنگی گزینه ها C | |||||||
| اوزان | 0.2 | 0.1 | 0.1 | 0.1 | 0.2 | 0.3 | مجموع |
| سرعت | ظرفیت | شتاب | هزینه | اطمینان | مانور | ||
| C12 | – | – | 0.10 | 0.10 | 0.20 | 0.30 | 0.70 |
| C13 | 0.20 | – | – | – | – | 0.30 | 0.50 |
| C14 | – | – | 0.10 | – | 0.20 | 0.30 | 0.60 |
| C21 | 0.20 | 0.10 | – | – | – | – | 0.30 |
| C23 | 0.20 | 0.10 | – | – | – | – | 0.30 |
| C24 | 0.20 | 0.10 | – | – | – | 0.30 | 0.60 |
| C31 | – | 0.10 | 0.10 | 0.10 | 0.20 | – | 0.50 |
| C32 | – | – | 0.10 | 0.10 | 0.20 | 0.30 | 0.70 |
| C34 | – | 0.10 | 0.10 | 0.10 | 0.20 | 0.30 | 0.80 |
| C41 | 0.20 | 0.10 | 0.10 | 0.10 | 0.20 | – | 0.70 |
| C42 | – | – | 0.10 | 0.10 | 0.20 | 0.30 | 0.70 |
| C43 | 0.20 | – | – | – | – | – | 0.20 |
حال با جایگزینی مجموع اوزان در ماتریس، ماتریس هماهنگی را به صورت زیر تشکیل می دهیم. به طور مثال مقدار 0.50 شاخص تفاوت C13 در سطر اول ستون دوم ماتریس قرار می گیرد.
| ماتریس هماهنگ C | |||
| – | 0.70 | 0.50 | 0.60 |
| 0.30 | – | 0.30 | 0.60 |
| 0.50 | 0.70 | – | 0.80 |
| 0.70 | 0.70 | 0.20 | – |
در این مرحله میانگین (حداقل آستانه) تمامی عناصر ماتریس را محاسبه می کنیم.
AVERAGE = (0.7+0.50+…)/12 = 0.55
حال ماتریس هماهنگی موثر را تشکیل می دهیم. اگر مقادیر ماتریس از میانگین کمتر باشد، 0 و اگر مقدار آن بیشتر باشد در ماتریس 1 قرار می دهیم. به طور مثال عنصر A12=0.7 از0.55 بیشتر است پس در ماتریس 1 قرار می دهیم.
| ماتریس F | |||
| – | 1 | 0 | 1 |
| 0 | – | 0 | 1 |
| 0 | 1 | – | 1 |
| 1 | 1 | 0 | – |
گام چهارم روش ELECTRE الکتره:
حال در این گام ماتریس ناهماهنگی را بر اساس روش ذکر شده محاسبه می کنیم. به طور مثال دو گزینه A1,A2 را با هم مقایسه می کنیم:
- برای هر گزینه 6 شاخص داریم. در بخش هماهنگی {C12={3,4,5,6 این شاخص ها به عنوان شاخص های هماهنگ تعیین شدند پس شاخص ها ناهماهنگی آن {D12={1,2 خواهد بود. شاخص های ناهماهنگ در جدول با رنگ قرمز مشخص شده اند.
- ابتدا بر اساس فرمول ذکر شده قدر مطلق تفاوت بین تمامی شاخص ها را حساب می کنیم. به طور مثال: |0.093-0.117| = 0.234 ، |0.037-0.066|=0.0293 و …
- حال که تمامی تفاوت ها را محاسبه نمودیم براساس فرمول ذکر شده، ماکسیمم شاخص های ناهماهنگ را محاسبه می کنیم. به طور مثال: MAX(0.243,0.293) = 0.293 تمامی این مقادیر در فیلد MAX Loss جدول قرار گرفته است.
- حال ماکسیمم هر ردیف محاسبه می شود که در جدول زیر با MAX Row مشخص شده است.
- در اتنها بر اساس فرمول MAX Loss/ Max Row تقسیم می شود تا مقدار شاخص ناهماهنگی بدست آید.
| سرعت | ظرفیت | شتاب | هزینه | اطمینان | مانور | MAX Loss | MAX Row | Loss/Row | |
| D12 | 0.0234 | 0.0293 | 0.0051 | 0.0092 | 0.0385 | 0.0894 | 0.0293 | 0.0894 | 0.3275 |
| D13 | 0.0093 | 0.0122 | 0.0025 | 0.0092 | 0.0385 | 0.0447 | 0.0385 | 0.0447 | 0.8607 |
| D14 | 0.0093 | 0.0073 | 0.0000 | 0.0046 | 0.0000 | 0.0894 | 0.0093 | 0.0894 | 0.1045 |
| D21 | 0.0234 | 0.0293 | 0.0051 | 0.0092 | 0.0385 | 0.0894 | 0.0894 | 0.0894 | 1 |
| D23 | 0.0327 | 0.0171 | 0.0076 | 0.0184 | 0.0770 | 0.0447 | 0.0770 | 0.0770 | 1 |
| D24 | 0.0140 | 0.0220 | 0.0051 | 0.0138 | 0.0385 | 0.0000 | 0.0385 | 0.0385 | 1 |
| D31 | 0.0093 | 0.0122 | 0.0025 | 0.0092 | 0.0385 | 0.0447 | 0.0447 | 0.0447 | 1 |
| D32 | 0.0327 | 0.0171 | 0.0076 | 0.0184 | 0.0770 | 0.0447 | 0.0327 | 0.0770 | 0.4248 |
| D34 | 0.0187 | 0.0049 | 0.0025 | 0.0046 | 0.0385 | 0.0447 | 0.0187 | 0.0447 | 0.4178 |
| D41 | 0.0093 | 0.0073 | 0.0000 | 0.0046 | 0.0000 | 0.0894 | 0.0894 | 0.0894 | 1 |
| D42 | 0.0140 | 0.0220 | 0.0051 | 0.0138 | 0.0385 | 0.0000 | 0.0220 | 0.0385 | 0.5708 |
| D43 | 0.0187 | 0.0049 | 0.0025 | 0.0046 | 0.0385 | 0.0447 | 0.0447 | 0.0447 | 1 |
حال با جایگزینی مجموع اوزان در ماتریس، ماتریس ناهماهنگی را به صورت زیر تشکیل می دهیم. به طور مثال مقدار 0.1045 شاخص D14 در ماتریس سطر اول، ستون سوم قرار می گیرد.
| ماتریس ناهماهنگ D | |||
| – | 0.33 | 0.86 | 0.10 |
| 1.00 | – | 1.00 | 1.00 |
| 1.00 | 0.42 | – | 0.42 |
| 1.00 | 0.57 | 1.00 | – |
در این مرحله میانگین (حداقل آستانه) تمامی عناصر ماتریس را محاسبه می کنیم.
AVERAGE = (0.33+0.86+…)/12 = 0.73
حال ماتریس ناهماهنگی موثر را تشکیل می دهیم. اگر مقادیر ماتریس از میانگین بیشتر باشد، 0 و اگر مقدار آن کمتر باشد در ماتریس 1 قرار می دهیم. به طور مثال عنصر A12=0.33 از0.73 کمتر است پس در ماتریس 1 قرار می دهیم.
| ماتریس G | |||
| – | 1 | 0 | 1 |
| 0 | – | 0 | 0 |
| 0 | 1 | – | 1 |
| 0 | 1 | 0 | – |
گام پنجم روش ELECTRE الکتره:
در این گام برای تعیین برتری ها دو ماتریس F و G در هم ضرب برداری می شوند. این به گونه ای است که وقتی هر دو مقدار 1 باشد جواب یک می گردد و در غیر این صورت جواب 0 خواهد بود.
| – | 1 | 0 | 1 |
| 0 | – | 0 | 0 |
| 0 | 1 | – | 1 |
| 0 | 1 | 0 | – |
در این مرحله تعداد 1 و 0 های هر ردیف شمرده می شود. مانند جدول زیر جمع یک ها در ستون Win و جمع صفرها در ستون loss و اختلاف آن ها در Different قرار می گیرد. سپس بر اساس ستون Different شاخص ها رتبه بندی می شوند.
| Win | Loss | Different | Rank | |
| 2 | 1 | 1 | 1 | A1 |
| 0 | 3 | -3 | 4 | A2 |
| 2 | 1 | 1 | 1 | A3 |
| 1 | 2 | -1 | 3 | A4 |
همان طور که مشاهده می شود شاخص های A1,A3 دارای رتبه اول می باشند که نمی توان در مورد برتری آنها از یکدیگر نظری داشت و در ادامه شاخص A4 و در نهایت A2 قرار می گیرد.
حال باید به تعداد گزینه های مساله ای که با آن مواجه هستیم گره رسم کنیم. برای رسم کمان بین این گره ها، اگر در ماتریس E بین دو گزینه مولفه 1 وجود داشت، از گره سطر مربوطه در ماتریس به گره ستون مربوطه در ماتریس یک فلش جهت دار رسم می کنیم. هر کدام که بیشترین خروجی را داشته باشند، از ترجیح و برتری بیشتری برخوردار است.
۳. تفاوت روش ELECTRE الکتره با روشهای دیگر
یکی از چالشهای روش روش ELECTRE الکتره نسبت به روش PROMETHEE، پیچیدگی در تعیین آستانهها و احتمال ایجاد چرخه در گراف تسلط است. با این حال، روش ELECTRE الکتره در شناسایی گزینههایی که در برخی معیارها “بسیار بد” هستند، بیرقیب است. این روش به جای ارائه یک رتبهبندی خطی ساده، یک “مجموعه برگزیده” از گزینهها را معرفی میکند که در مسائل رتبهبندی گزینهها بسیار ارزشمند است.
سوالات متداول
چرا شاخص ناهماهنگی در روش ELECTRE الکتره حیاتی است؟
چون این شاخص اجازه نمیدهد قدرت زیاد یک گزینه در یک معیار، ضعف فاحش آن در معیار دیگر را بپوشاند.
آستانه هماهنگی (Threshold) چگونه تعیین میشود؟
معمولاً از میانگین مقادیر ماتریس هماهنگی به دست میآید، اما میتواند بر اساس نظر خبره نیز تغییر کند.
آیا ELECTRE الکتره همیشه یک رتبه اول قطعی دارد؟
خیر؛ ممکن است خروجی روش ELECTRE الکتره مجموعهای از چند گزینه برتر باشد که نسبت به هم برتری ندارند اما بر تمام گزینههای دیگر مسلط هستند.
نتیجهگیری و جمعبندی نهایی
روش ELECTRE به عنوان یکی از کلاسیکترین و در عین حال دقیقترین روشها در دسته رتبهبندی گزینهها، با تکیه بر مفاهیم روابط برتری، نگاهی عمیق به فرآیند انتخاب ارائه میدهد. قدرت این روش در مدلسازی همزمان شواهد موافق (هماهنگی) و مخالف (ناهماهنگی) نهفته است که اجازه میدهد تصمیمگیرنده از ریسکهای پنهان در پس امتیازات میانگین عبور کند. این رویکرد در مباحث تحقیق در عملیات، روش ELECTRE الکتره را به ابزاری استراتژیک برای حذف گزینههای غیربهینه و تمرکز بر گزینههای با عملکرد متوازن تبدیل کرده است.
پیادهسازی این متد در پروژههای تحقیقاتی و بخش آمار و تحلیل داده، نیازمند دقت بالا در تشکیل ماتریسهای تسلط و تفسیر گرافهای خروجی است. محققانی که از روش ELECTRE الکتره استفاده میکنند، قادرند تحلیلهای “غربالگری” قدرتمندی ارائه دهند که در محیطهای صنعتی و مدیریتی بسیار پرطرفدار است. ترکیب این روش با متدهای مدرن وزندهی معیارها مانند روش BWM، به ویژه در شرایطی که معیارهای کیفی و کمی در کنار هم قرار دارند، یک مدل تصمیمگیری بسیار منعطف و قابل دفاع ایجاد میکند.
در نهایت، برای مدیریت پیچیدگیهای عددی و ترسیم دقیق گرافهای تسلط، بهرهگیری از فایلهای تخصصی در آکادمی نرمافزار فرابگیر یک ضرورت به شمار میآید. استفاده از ابزارهای آماده نه تنها سرعت انجام پروژه را دوچندان میکند، بلکه امکان تمرکز بر تحلیلهای حساسیت آستانهها را فراهم میآورد. ما معتقدیم یادگیری روش روش ELECTRE الکتره ، دانش شما را در حوزه تصمیمگیری چندمعیاره (MCDM) به سطح حرفهای میرساند و شما را قادر میسازد تا در مسائل پیچیده، انتخابی فراتر از محاسبات ساده ریاضی داشته باشید.
