آموزش جامع روش PROMETHEE II
روش PROMETHEE II به عنوان تکاملیافتهترین نسخه از خانواده روشهای پرومتی، با هدف رفع ابهام در رتبهبندی گزینهها معرفی شد. در حالی که نسخه اول این روش (PROMETHEE I) ممکن بود برخی گزینهها را به دلیل تضاد در جریانهای ورودی و خروجی “غیرقابل مقایسه” تشخیص دهد، نسخه دوم با معرفی مفهوم “جریان خالص”، یک رتبهبندی خطی و کامل ارائه میدهد. این ویژگی باعث شده است که در پروژههای تحقیق در عملیات، زمانی که نیاز به انتخاب یک گزینه واحد یا رتبهبندی تمامی موارد است، PROMETHEE II اولویت اول محققان باشد.
منطق زیربنایی این روش در ساختار تصمیمگیری چندمعیاره (MCDM)، بر پایه ترازوی میان قدرت و ضعف گزینهها استوار است. در واقع، پرومتی ۲ معتقد است که برای رسیدن به یک تصمیم نهایی، باید برتریهای یک گزینه بر دیگران را در مقابل ضعفهای آن قرار داد تا برایند نهایی (جریان خالص) مشخص شود. این رویکرد دقیق، به تصمیمگیرندگان در بخش آموزش مدیریت اجازه میدهد تا با اطمینان کامل از حذف اثرات منفی، گزینهای را انتخاب کنند که در مجموع بیشترین مطلوبیت را ایجاد میکند.
در سایت فرابگیر، ما این متد را به عنوان ابزاری تخصصی برای تحلیلهای حساس و استراتژیک معرفی میکنیم. PROMETHEE II با ترکیب وزنهای حاصل از وزندهی معیارها و توابع ترجیح دقیق، مدلی را میسازد که نه تنها رتبه اول را مشخص میکند، بلکه فاصله کیفی میان گزینهها را نیز به شکلی عددی و قابل مقایسه در بخش آمار و تحلیل داده به نمایش میگذارد. این روش، پلی میان قضاوتهای کیفی خبرگان و محاسبات دقیق ریاضی در حوزه رتبهبندی گزینهها است.
آنچه می خوانید
روش PROMETHEE II (پرومتی 2) چیست؟
در دنیای پیچیده امروز، انتخاب ایدهآلترین گزینه از میان انبوه گزینه ها، دغدغهای همیشگی برای انسان بوده است. در این میان، روشهای تصمیمگیری چندمعیاره (MADM) به عنوان ابزاری قدرتمند، یاریگر انسان در حل این چالش بزرگ هستند. روش PROMETHEE II (پرومتی 2) به عنوان یکی از روشهای نوین MADM، با رویکردی کارآمد و دقیق، به رتبهبندی و انتخاب بهترین گزینه کمک میکند.
روش PROMETHEE II (پرومتی 2) در دهه 1980 توسط دو استاد بلژیکی به نامهای ژان پیر برنز و برتراند مارسکال ابداع شد. این روش در واقع تکامل یافته روش پرومته 1 است و با در نظر گرفتن ترجیحات و بیتفاوتیها، به رتبهبندی کامل گزینهها میپردازد.
اصول و مبانی روش PROMETHEE II (پرومتی 2)
- شاخصها: معیارهایی که برای ارزیابی گزینهها به کار میروند.
- گزینهها: گزینه هایی که باید از بین آنها بهترین انتخاب شود.
- ترجیح: تمایل به انتخاب یک گزینه به جای گزینه دیگر.
- بیتفاوتی: عدم تمایل به انتخاب بین دو گزینه.
- آستانه بیتفاوتی: حداقل تفاوتی که بین دو گزینه باید وجود داشته باشد تا ترجیح ایجاد شود.
- آستانه ترجیح: حداقل تفاوتی که بین دو گزینه باید وجود داشته باشد تا ترجیح قوی ایجاد شود.
- تابع ترجیح: تابعی که میزان ترجیح یک گزینه به گزینه دیگر را نشان میدهد.
کاربردهای روش PROMETHEE II (پرومتی 2)
روش PROMETHEE II (پرومتی 2) به عنوان ابزاری قدرتمند در تصمیمگیری چندمعیاره، در طیف وسیعی از مسائل و حوزهها کاربرد دارد. برخی از کاربردهای این روش عبارتند از:
انتخاب سبد سرمایهگذاری:
در این مسأله، سرمایهگذار باید از بین مجموعهای از اوراق بهادار، بهترین سبد سرمایهگذاری را با توجه به معیارهایی مانند ریسک، بازده، نقدشوندگی و … انتخاب کند. روش PROMETHEE II (پرومتی 2) میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای سرمایهگذار، به انتخاب ایدهآلترین سبد سرمایهگذاری کمک کند.
انتخاب پیمانکار:
در این مسأله، کارفرما باید از بین مجموعهای از پیمانکاران، بهترین پیمانکار را برای انجام یک پروژه با توجه به معیارهایی مانند قیمت، کیفیت، سابقه کار، زمانبندی و … انتخاب کند. روش PROMETHEE II (پرومتی 2) میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای کارفرما، به انتخاب ایدهآلترین پیمانکار کمک کند.
انتخاب محل احداث کارخانه:
در این مسأله، باید از بین مجموعهای از مکانهای مختلف، بهترین محل برای احداث یک کارخانه با توجه به معیارهایی مانند دسترسی به مواد اولیه، دسترسی به بازار، زیرساختها، هزینهها و … انتخاب شود. روش PROMETHEE II (پرومتی 2) میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای سرمایهگذار، به انتخاب ایدهآلترین محل برای احداث کارخانه کمک کند.
انتخاب طرحهای تحقیقاتی:
در این مسأله، باید از بین مجموعهای از طرحهای تحقیقاتی، بهترین طرحها با توجه به معیارهایی مانند نوآوری، اهمیت، امکانپذیری، هزینه و … انتخاب شود. روش پرومته 2 میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای تصمیمگیرندگان، به انتخاب ایدهآلترین طرحهای تحقیقاتی کمک کند.
انتخاب شغل:
در این مسأله، فرد باید از بین مجموعهای از شغلهای مختلف، بهترین شغل را با توجه به معیارهایی مانند حقوق، مزایا، علاقه، مهارت و … انتخاب کند. روش PROMETHEE II (پرومتی 2) میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای فرد، به انتخاب ایدهآلترین شغل کمک کند.
در این مسأله، فرد باید از بین مجموعهای از دانشگاههای مختلف، بهترین دانشگاه را با توجه به معیارهایی مانند رتبه، رشته تحصیلی، شهریه، امکانات و … انتخاب کند. روش PROMETHEE II (پرومتی 2) میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای فرد، به انتخاب ایدهآلترین دانشگاه کمک کند.
انتخاب خودرو:
در این مسأله، فرد باید از بین مجموعهای از خودروهای مختلف، بهترین خودرو را با توجه به معیارهایی مانند قیمت، مصرف سوخت، ایمنی، شتاب و … انتخاب کند. روش PROMETHEE II (پرومتی 2) میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای فرد، به انتخاب ایدهآلترین خودرو کمک کند.

علاوه بر موارد ذکر شده، روش PROMETHEE II (پرومتی 2) در زمینههای دیگری مانند انتخاب روش درمانی، انتخاب هتل، انتخاب رستوران و … نیز کاربرد دارد. انتخاب معیارهای مناسب و تعیین آستانههای بیتفاوتی و ترجیح، نقش مهمی در کارایی و دقت روش PROMETHEE II (پرومتی 2) دارد.
مزایای روش PROMETHEE II (پرومتی 2)
- سادگی و سهولت استفاده
- کارایی در شرایط عدم قطعیت و اطلاعات ناقص
- توجه به ترجیحات و بیتفاوتیهای تصمیمگیرنده
- ارائه رتبهبندی کامل گزینهها
- قابلیت استفاده در طیف وسیعی از مسائل
معایب روش PROMETHEE II (پرومتی 2)
- نیاز به محاسبات نسبتاً پیچیده
- عدم وجود ضمانت برای یافتن جواب ایدهآل در همه مسائل
- وابستگی نتایج به انتخاب تابع ترجیح
مراحل روش PROMETHEE II (پرومتی 2)
- تعریف گزینهها و معیارها: در این مرحله، باید گزینهها و معیارهای مورد نظر برای انتخاب ایدهآلترین گزینه مشخص شوند.
- تشکیل ماتریس تصمیم: در این مرحله، باید امتیاز هر گزینه در هر معیار مشخص شود.
- تعیین آستانههای بیتفاوتی و ترجیح: در این مرحله، باید آستانههای بیتفاوتی و ترجیح برای هر معیار مشخص شود.
- محاسبه ماتریس جریان ورودی و خروجی: در این مرحله، ماتریسهای جریان ورودی و خروجی با توجه به ترجیحات و بیتفاوتیها محاسبه میشوند.
- محاسبه شاخص پرومته: در این مرحله، شاخص پرومته برای هر گزینه محاسبه میشود.
- رتبهبندی گزینهها: در این مرحله، گزینهها بر اساس شاخص پرومته رتبهبندی میشوند.
محدودیتهای روش PROMETHEE II (پرومتی 2)
- این روش برای حل مسائل با تعداد زیادی گزینه مناسب نیست.
- این روش برای حل مسائل با معیارهای کیفی نامناسب است.
نرمافزارهای مرتبط
- Visual PROMETHEE
- Promethee GAIA
- Decision Lab
الگوریتم حل روش PROMETHEE II (پرومتی 2)
گام اول: تعریف مسئله و شناسایی گزینه ها
- در این مرحله، مسئله مورد نظر به طور کامل تعریف شده و گزینه های مختلف برای انتخاب مشخص می شوند.
- به عنوان مثال، می خواهیم از بین 3 خودرو A، B و C با توجه به 4 معیار قیمت، سرعت، مصرف سوخت و ایمنی، بهترین خودرو را انتخاب کنیم.
گام دوم:تعیین معیارها و شاخص ها
- معیارها، ویژگی های اصلی هستند که برای ارزیابی گزینه ها استفاده می شوند.
- شاخص ها، مقیاس های اندازه گیری هر معیار هستند.
- برای مثال، معیار قیمت می تواند با شاخص “قیمت نهایی” و معیار سرعت می تواند با شاخص “حداکثر سرعت” اندازه گیری شود.
گام سوم:تعیین ترجیحات و آستانه ها
- در این مرحله، ترجیحات تصمیم گیرنده برای هر معیار مشخص می شود.
- ترجیحات می تواند به صورت “بیشتر بهتر” یا “کمتر بهتر” باشد.
- آستانه های بیتفاوتی و ترجیح نیز برای هر معیار تعیین می شوند.
- آستانه بیتفاوتی، حداقل تفاوتی است که بین دو گزینه باید وجود داشته باشد تا ترجیح ایجاد شود.
- آستانه ترجیح، حداقل تفاوتی است که بین دو گزینه باید وجود داشته باشد تا ترجیح قوی ایجاد شود.
گام چهارم: محاسبه ماتریس ترجیحات
- ماتریس ترجیحات، نشان دهنده ترجیح هر گزینه نسبت به هر گزینه دیگر است.
- برای محاسبه ماتریس ترجیحات، از تابع ترجیح استفاده می شود.
- تابع ترجیح، تابعی است که میزان ترجیح یک گزینه به گزینه دیگر را نشان می دهد.
ماتریس ترجیحات نشان دهنده ترجیح هر گزینه نسبت به هر گزینه دیگر است. برای محاسبه ماتریس ترجیحات، از تابع ترجیح استفاده می شود. تابع ترجیح، تابعی است که میزان ترجیح یک گزینه به گزینه دیگر را نشان می دهد.
فرمول ماتریس ترجیحات:
P_{ij} = f(d_j - d_i)در این فرمول:
P_{ij}: ترجیح گزینهiنسبت به گزینهjf(.): تابع ترجیحd_i: مقدار شاخصiبرای گزینهin: تعداد گزینه ها
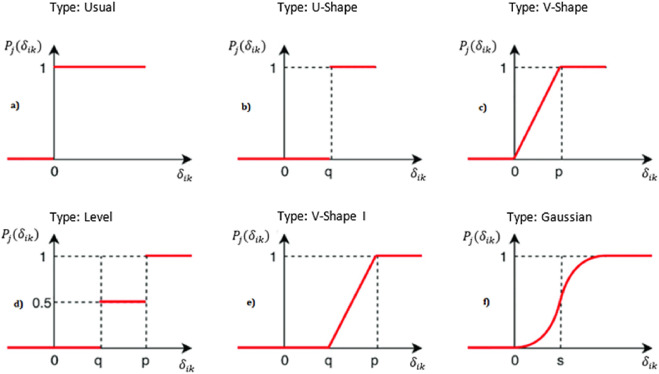
توابع ترجیح:
توابع ترجیح مختلفی وجود دارد که می توان از آنها در روش PROMETHEE II (پرومتی 2) استفاده کرد. برخی از رایج ترین توابع ترجیح عبارتند از:
- تابع ترجیح خطی:
f(x) = x
- تابع ترجیح گاوس:
f(x) = e^(-x^2/2σ^2)
- تابع ترجیح شبه خطی:
f(x) =
{
x, if x > q
0, if x <= q
}
در این فرمول:
σ: انحراف معیارq: آستانه بیتفاوتی
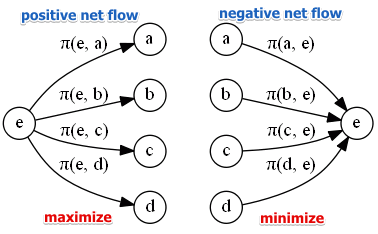
گام پنجم: محاسبه ماتریس جریان ورودی و خروجی
ماتریس جریان ورودی (Φ+) نشان میدهد که هر گزینه چقدر از سایر گزینهها ترجیح داده میشود. ماتریس جریان خروجی (Φ-) نشان میدهد که هر گزینه چقدر توسط سایر گزینهها ترجیح داده میشود.
Φ+ = 1/m[π(a,b)]
Φ- = 1/m[π(b,a)]گام ششم: محاسبه شاخصهای پرومته
شاخص پرومته I برای هر گزینه، تفاضل ماتریسهای جریان ورودی و خروجی آن گزینه است.
I(a) = Φ+(a) - Φ-(a)گام هفتم: رتبه بندی گزینه ها:
- گزینه ها بر اساس شاخص های Φ و Ψ رتبه بندی می شوند.
- به طور کلی، گزینه ای که بیشترین مقدار Φ و کمترین مقدار Ψ را داشته باشد، بهترین گزینه است.
در این روش، گزینهای بر گزینه دیگر برتر است که جریان خالص بزرگتری داشته باشد. این مقدار همواره بین ۱- و ۱+ قرار دارد. به دلیل حساسیت بالای این تفاضل در رتبهبندی نهایی، استفاده از فایل اکسل روش PROMETHEE در آکادمی نرمافزار فرابگیر، بهترین راه برای اطمینان از صحت نتایج است.
مثال روش PROMETHEE II (پرومتی 2)
فردی قصد دارد كه یكی از 4 مدل گوشی همراه سامسونگ، ال جی، سونی، اپل را خریداری كند. برای این گوشی ها 4 شاخص در نظر گرفته شده است. با روش پرومته 2 این رتبه بندی را انجام می دهیم.
| اوزان | 0.35 | 0.25 | 0.25 | 0.15 |
| نوع | منفی | مثبت | مثبت | مثبت |
| گزینه ها | قیمت | حافظه | دوربین | زیبایی |
| M1 | 250 | 16 | 12 | 5 |
| M2 | 200 | 16 | 8 | 3 |
| M3 | 300 | 32 | 16 | 4 |
| M4 | 275 | 32 | 8 | 2 |
گام اول: نرمال سازی ماتریس
برای از بین بردن اثر علامت شاخص ها ابتدا ماتریس را نرمال می کنیم. می توانیم از انواع روش های نرمال سازی نرم، اقلیدسی و غیره برای این منظور استفاده کنیم.
| ماتریس تصمیم گیری نرمال | ||||
| گزینه ها | قیمت | حافظه | دوربین | زیبایی |
| M1 | 0.50 | 0.00 | 0.50 | 1.00 |
| M2 | 1.00 | 0.00 | 0.00 | 0.33 |
| M3 | 0.00 | 1.00 | 1.00 | 0.67 |
| M4 | 0.25 | 1.00 | 0.00 | 0.00 |
گام دوم: محاسبه اختلاف بین گزینه ها
در این گام اختلاف هر یک از گزینه ها را با همدیگر محاسبه می کنیم.
| گزینه ها | قیمت | حافظه | دوربین | زیبایی |
| M1-M2 | -0.50 | 0.00 | 0.50 | 0.67 |
| M1-M3 | 0.50 | -1.00 | -0.50 | 0.33 |
| M1-M4 | 0.25 | -1.00 | 0.50 | 1.00 |
| M2-M1 | 0.50 | 0.00 | -0.50 | -0.67 |
| M2-M3 | 1.00 | -1.00 | -1.00 | -0.33 |
| M2-M4 | 0.75 | -1.00 | 0.00 | 0.33 |
| M3-M1 | -0.50 | 1.00 | 0.50 | -0.33 |
| M3-M2 | -1.00 | 1.00 | 1.00 | 0.33 |
| M3-M4 | -0.25 | 0.00 | 1.00 | 0.67 |
| M4-M1 | -0.25 | 1.00 | -0.50 | -1.00 |
| M4-M2 | -0.75 | 1.00 | 0.00 | -0.33 |
| M4-M3 | 0.25 | 0.00 | -1.00 | -0.67 |
گام سوم: محاسبه ترجحات بین گزینه
برای محاسبه ترجیحات، از انواع تابع ترجیح می توان استفاده کرد. در این مثال از تابع ترجیح عادی استفاده شده است.
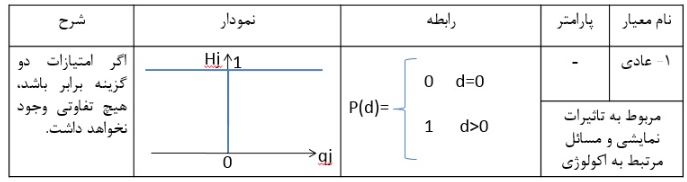
بدین معنی که گزینه هایی که اختلاف آنها کمتر یا مساوی صفر باشد مقدار صفر و سایر گزینه ها مقدار اختلاف را به خود اختصاص می دهند.
| اوزان | 0.35 | 0.25 | 0.25 | 0.15 |
| گزینه ها | قیمت | حافظه | دوربین | زیبایی |
| M1-M2 | 0.00 | 0.00 | 0.50 | 0.67 |
| M1-M3 | 0.50 | 0.00 | 0.00 | 0.33 |
| M1-M4 | 0.25 | 0.00 | 0.50 | 1.00 |
| M2-M1 | 0.50 | 0.00 | 0.00 | 0.00 |
| M2-M3 | 1.00 | 0.00 | 0.00 | 0.00 |
| M2-M4 | 0.75 | 0.00 | 0.00 | 0.33 |
| M3-M1 | 0.00 | 1.00 | 0.50 | 0.00 |
| M3-M2 | 0.00 | 1.00 | 1.00 | 0.33 |
| M3-M4 | 0.00 | 0.00 | 1.00 | 0.67 |
| M4-M1 | 0.00 | 1.00 | 0.00 | 0.00 |
| M4-M2 | 0.00 | 1.00 | 0.00 | 0.00 |
| M4-M3 | 0.25 | 0.00 | 0.00 | 0.00 |
گام چهارم: محاسبه ماتریس ترجیح وزن دار
در این گام اوزان هر یک از معیارها در مقدار ترجیح آن ضرب و ماتریس ترجیح وزن دار محاسبه می شود. در ادامه مقدار ترجیح وزن دار هر یک از اختلافات با هم جمع می شود
| گزینه ها | قیمت | حافظه | دوربین | زیبایی | SUM |
| M1-M2 | 0.000 | 0.000 | 0.125 | 0.100 | 0.2250 |
| M1-M3 | 0.175 | 0.000 | 0.000 | 0.050 | 0.2250 |
| M1-M4 | 0.088 | 0.000 | 0.125 | 0.150 | 0.3625 |
| M2-M1 | 0.175 | 0.000 | 0.000 | 0.000 | 0.1750 |
| M2-M3 | 0.350 | 0.000 | 0.000 | 0.000 | 0.3500 |
| M2-M4 | 0.263 | 0.000 | 0.000 | 0.050 | 0.3125 |
| M3-M1 | 0.000 | 0.250 | 0.125 | 0.000 | 0.3750 |
| M3-M2 | 0.000 | 0.250 | 0.250 | 0.050 | 0.5500 |
| M3-M4 | 0.000 | 0.000 | 0.250 | 0.100 | 0.3500 |
| M4-M1 | 0.000 | 0.250 | 0.000 | 0.000 | 0.2500 |
| M4-M2 | 0.000 | 0.250 | 0.000 | 0.000 | 0.2500 |
| M4-M3 | 0.088 | 0.000 | 0.000 | 0.000 | 0.0875 |
گام پنجم: محاسبه ماتریس جریان ورودی و خروجی
در ادامه با توجه به مجموع وزن های بدست آمده ماتریس ارتباط بین گزینه ها تشکیل می شود.
| گزینه ها | M1 | M2 | M3 | M4 | ф+ |
| M1 | 0.00 | 0.23 | 0.23 | 0.36 | 0.8125 |
| M2 | 0.18 | 0.00 | 0.35 | 0.31 | 0.8375 |
| M3 | 0.38 | 0.55 | 0.00 | 0.35 | 1.2750 |
| M4 | 0.25 | 0.25 | 0.09 | 0.00 | 0.5875 |
| ф- | 0.8000 | 1.0250 | 0.6625 | 1.0250 |
گام ششم: محاسبه شاخصهای پرومته
شاخص پرومته II برای هر گزینه، تفاضل ماتریسهای جریان ورودی و خروجی آن گزینه است.
| گزینه ها | ф+ | ф- | ф | رتبه بندی |
| M1 | 0.2708 | 0.2667 | 0.0042 | 2 |
| M2 | 0.2792 | 0.3417 | -0.0625 | 3 |
| M3 | 0.4250 | 0.2208 | 0.2042 | 1 |
| M4 | 0.1958 | 0.3417 | -0.1458 | 4 |
گام هفتم: رتبه بندی گزینه ها:
- گزینه ها بر اساس شاخص های Φ و Ψ رتبه بندی می شوند.
- به طور کلی، گزینه ای که بیشترین مقدار Φ و کمترین مقدار Ψ را داشته باشد، بهترین گزینه است.
مشاهده می شود که گزینه سوم بهترین گزینه و گزینه چهارم بدترین انتخاب است.
تفاوت کلیدی PROMETHEE I و II
بزرگترین مزیت PROMETHEE II نسبت به نسخه ۱، حذف حالت “عدم قابلیت مقایسه” (Incomparability) است. در نسخه ۱، اگر گزینهای در جریان خروجی قوی و در جریان ورودی هم ضعیف بود، سیستم نمیتوانست رتبه قطعی صادر کند. اما در پرومتی ۲، با کسر کردن این دو مقدار، یک عدد واحد به دست میآید که تکلیف رتبهبندی را روشن میکند. این روش در مقایسه با روش ELECTRE که ممکن است خروجیهای چندگانه داشته باشد، بسیار قاطعتر عمل میکند.
سوالات متداول
آیا PROMETHEE II همیشه نتایج مشابه TOPSIS ارائه میدهد؟
خیر؛ به دلیل استفاده از توابع ترجیح و آستانهها، پرومتی ۲ معمولاً نتایج دقیقتری نسبت به روش TOPSIS در مواجهه با ترجیحات کیفی خبرگان دارد.
جریان خالص منفی به چه معناست؟
اگر جریان خالص گزینهای منفی شود، به این معناست که میزان ضعف آن گزینه در برابر رقبا، بیشتر از قدرت و برتریهای آن است.
بهترین تابع ترجیح برای معیارهای کمی چیست؟
معمولاً تابع شماره ۵ (Linear) یا شماره ۶ (Gaussian) به دلیل دقت در مدلسازی فواصل عددی پیشنهاد میشود.
نتیجهگیری و جمعبندی نهایی
روش PROMETHEE II به عنوان ابزاری قاطع در دسته رتبهبندی گزینهها، با ارائه جریان خالص، ابهامات موجود در تصمیمگیریهای چندمعیاره را به حداقل رسانده است. این متد با تبدیل روابط پیچیده برتری به یک شاخص عددی واحد، فرآیند انتخاب را برای مدیران تسهیل کرده و خروجیهایی شفاف و قابل دفاع تولید میکند. قدرت این روش در حفظ تعادل میان معیارهای متضاد، آن را به یکی از محبوبترین تکنیکها در پژوهشهای تحقیق در عملیات تبدیل کرده است.
تسلط بر پیادهسازی این روش در بخش آمار و تحلیل داده، به محقق اجازه میدهد تا تحلیلهای عمیقی از جایگاه هر گزینه نسبت به میانگین جامعه ارائه دهد. ترکیب هوشمندانه توابع ترجیح با اوزان استخراج شده از روش BWM، مدلی را ایجاد میکند که نه تنها رتبه نهایی را مشخص میسازد، بلکه پایداری آن رتبه را در برابر تغییرات کوچک در دادهها تضمین مینماید. این سطح از تحلیل، اعتبار پروژههای شما را در سطح ژورنالهای معتبر علمی به شدت ارتقا میدهد.
در نهایت، پیشنهاد میشود برای اجرای بدون نقص این الگوریتم، از منابع آموزشی و ابزارهای آکادمی نرمافزار فرابگیر بهره ببرید. استفاده از فایلهای محاسباتی آماده، ریسک خطاهای انسانی در محاسبه جریانهای مثبت و منفی را حذف کرده و فرصت بیشتری برای تمرکز بر تفسیر استراتژیک نتایج فراهم میآورد. ما در فرابگیر بر این باوریم که PROMETHEE II نقطه اوج دقت در تصمیمگیری چندمعیاره (MCDM) است که هر پژوهشگر حرفهای باید در جعبه ابزار تحلیلی خود داشته باشد.
