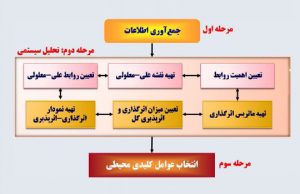
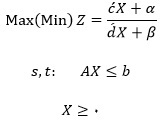محاسبه نرخ ناسازگاری در AHP فازی
نرخ ناسازگاری شاخصی است که میزان سازگاری پاسخ های خبرگان به ارزیابی ها و مقایسات زوجی را اندازه گیری می کند. به عبارت دیگر با کمک شاخص نرخ ناسازگاری می توان پی برد که بین مقایسه های دو به دو و زوجی در پرسشنامه های ما سازگاری وجود دارد یا خیر.
پایایی در پرسشنامه های AHP
گاهی برخی دانشجویان می پرسند که پایایی پرسشنامه های روش تحلیل سلسله مراتبی را چطور باید اندازه گیری کرد؟ در پاسخ بیان می گردد که در پرسشنامه های تحلیل سلسله مراتبی یا روش AHP موضوعی به نام پایایی، آنطوری که در پرسشنامه های معمول نرم افزار SPSS (که معمولا گزینه های 5 تایی طیف لیکرت دارد)، مطرح است وجود ندارد.
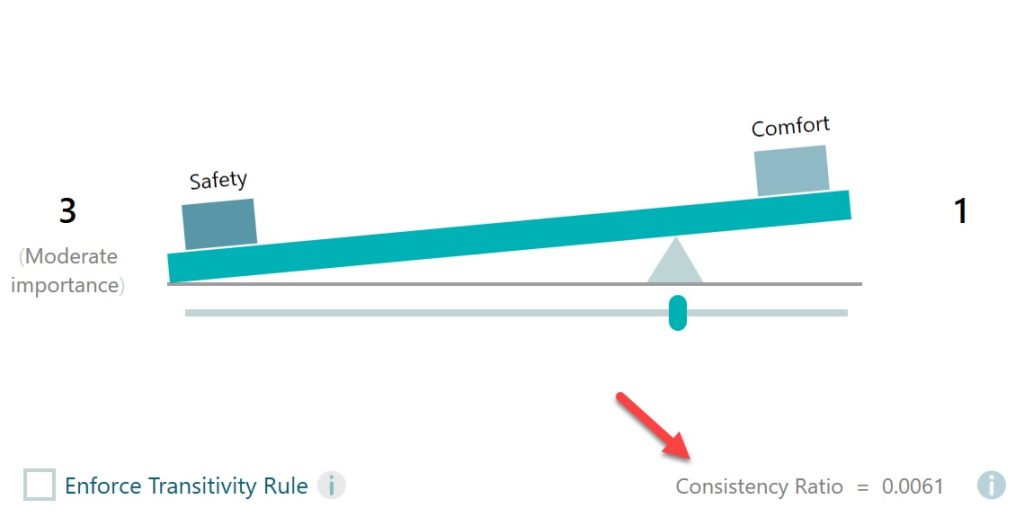
این وضعیت در خصوص پرسشنامه های روش ANP و AHP فازی، نیز صدق می کند. یعنی ما برای پرسشنامه مقایسه زوجی شاخص سنجش پایایی یا روایی، به مانند ضریب پایایی آلفای کرونباخ نداریم. بلکه به جای مفهوم پایایی در پرسشنامه های ahp، از مفهوم نرخ ناسازگاری استفاده می شود.
تعریف نرخ ناسازگاری
نرخ ناسازگاری شاخصی است که مقدار آن نشان دهنده تناقضات و ناسازگاری های احتمالی در ماتریس مقایسات زوجی است. بنابر نظر آقای ساعتی بنیانگذار روش AHP، چنانچه نرخ ناسازگاری کمتر از 0.1 باشد، سازگاری ماتریس مقایسات مورد تایید بوده و قابل قبول می باشند. اما در صورتی که نرخ ناسازگاری بزرگتر از 0.1 باشد، نشان دهنده تناقض در ارزیابی ها و قضاوت های خبرگان می باشد.
محاسبه نرخ ناسازگاری در AHP فازی محاسبه نرخ ناسازگاری در AHP فازی محاسبه نرخ ناسازگاری در AHP فازی
نمونه مقایسه زوجی سازگار چنین است: اگر بگوییم A از B بهتر است و B از C بهتر است، در نتیجه A نسبت به C خیلی بهتر است.
مثال زیر مفهوم نرخ ناسازگاری را روشن خواهد کرد.
فرض کنید تصمیم گیرنده مقایسات زوجی زیر را در اختیار ما قرار داده است:
- دید فروشگاه های مرکز فروش 2 برابر فروشگاه های سیتی سنتر است.
- دید فروشگاه های سیتی سنتر 3 برابر فروشگاه های شهرک صنعتی است.
- دید فروشگاه های شهرک صنعتی 4 برابر فروشگاه های مرکز فروش است.
عبارت سوم ناسازگار است. زیرا همانگونه که در دو عبارت اول بیان شده، شهرک صنعتی 6 برابر بیشتر از مرکز فروش در دید است (2*3). تا حدی ناسازگاری طبیعی و قابل قبول است و AHP برای اینکه اجازه بروز این ناسازگاری را بدهد، تا 10 درصد (0.1) ناسازگاری را مجاز می داند.
اهمیت محاسبه نرخ ناسازگاری
تجربه انجام دهها مورد تحلیل سلسله مراتبی به ما ثابت کرده است که این شاخص، شاخص معتبری برای سنجش واقعی بودن پاسخها به پرسشنامه های AHP است. اگر پاسخگو به درستی متوجه مقایسه ها و سوالات نباشد و بدون دقت پاسخ دهد به احتمال خیلی زیاد نرخ ناسازگاری از حد مجاز 0.1 عبور خواهد کرد.
تقریبا بعید است یک ماتریس مقایسات زوجی بدون دقت و به صورت تصادفی تکمیل شود اما نرخ ناسازگاری آن در محدوده مجاز باشد. بنابراین در تحلیل سلسله مراتبی، محاسبه و اعلام نرخ ناسازگاری یک نیاز جدی و ضروری است که مورد توافق همگان می باشد.
محاسبه نرخ ناسازگاری در AHP فازی
دو پژوهشگر به نام گاگوس و بوچر (۱۹۹۸) روشی را برای محاسبه درجه سازگاری ماتریسهای مقایسات زوجی فازی ارائه نمودهاند. در این روش به منظور بررسی سازگاری، لازم است گام های زیر را انجام دهیم.
محاسبه نرخ ناسازگاری در AHP فازی محاسبه نرخ ناسازگاری در AHP فازی محاسبه نرخ ناسازگاری در AHP فازی
مراحل محاسبه نرخ سازگاری گوگوس و بوچر
مرحله 1: تشکیل دو ماتریس فازی
در مرحله اول ماتریس مثلثی فازی را به دو ماتریس تقسیم کنید. ماتریس اول از اعداد میانی قضاوت های مثلثی تشکیل می شود و ماتریس دوم شامل میانگین هندسی حدود بالا و پایین اعداد مثلثی می شود.
ماتریس Am از مقادیر میانی ترجیحات خبرگان تشکیل میشود.
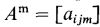
ماتریس Ag از میانگین کران بالا و پایین TFN تشکیل میشود.
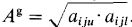
مرحله 2: محاسبه بردار وزن
بردار وزن هر ماتریس را با استفاده از روش ساعتی به ترتیب زیر محاسبه کنید.
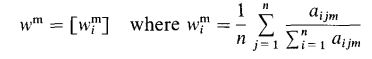
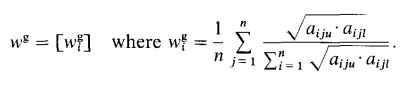
مرحله 3: محاسبه مقدار ویژه
بزرگترین مقدار ویژه برای هر ماتریس از طریق زیر محاسبه می شود.
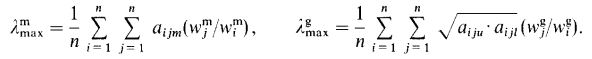
محاسبه نرخ ناسازگاری در AHP فازی محاسبه نرخ ناسازگاری در AHP فازی محاسبه نرخ ناسازگاری در AHP فازی
مرحله 4: شاخص های سازگاری (CI)
در ادامه به دنبال روش ساعتی، شاخص های سازگاری (CI) که نشان دهنده انحراف از سازگاری کامل هستند، توسط روابط زیر محاسبه می شود.
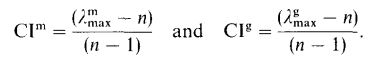
مرحله 5: محاسبه نرخ ناسازگاری
ساعتی برای بهدست آوردن مقادیر شاخص های تصادفی (RI)، ۱۰۰ ماتریس را با اعداد تصادفی و با شرط متقابل بودن ماتریس ها تشکیل داده و مقادیر ناسازگاری و میانگین آنها را محاسبه نمود. اما از آنجا که مقادیر عددی مقایسات فازی همواره عدد صحیح نیستند و حتی در این صورت هم میانگین هندسی، آنها را عموماً به اعداد غیرصحیح تبدیل میکند، حتی در صورت استفاده از مقیاس (۹-۱) ساعتی نیز نمی توان از جدول شاخصهای تصادفی (RI) ساعتی استفاده کرد.
بنابراین گوگوس و بوچر با تولید ۴۰۰ ماتریس تصادفی مجدداً جدول شاخص های تصادفی (RI) را برای ماتریسهای مقایسات زوجی فازی تولید کردند.
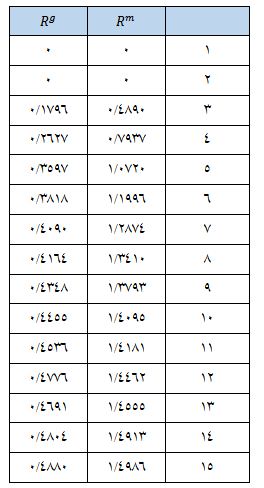
برای محاسبه نرخ ناسازگاری (CR)، شاخص CI را بر مقدار شاخص تصادفی (RI) تقسیم کنید. در صورتی که مقدار حاصل کمتر از ۰/۱ باشد، ماتریس سازگار و قابل استفاده تشخیص داده می شود.
CR = CI / RI
روشن است در پایان دو نرخ ناسازگاری وجود خواهد داشت که با CRm و CRg نمایش داده میشود. اگر هر دو روش نرخ ناسازگاری را بالای ۰٫۱ نشان دهد باید با تجدیدنظر در نتایج از خبرگان خواسته شود مجدداً ماتریسها را تکمیل کنند. همچنین حتی اگر یکی از دو مقدار هم از آستانه ۰٫۱ بزرگتر باشد توصیه اکید آن است که مقایسهها از نو انجام شود.
محاسبه نرخ ناسازگاری در AHP فازی محاسبه نرخ ناسازگاری در AHP فازی محاسبه نرخ ناسازگاری در AHP فازی
مثال محاسبه نرخ ناسازگاری در AHP فازی
فرض کنید می خواهیم برای ماتریس زیر نرخ ناسازگاری را محاسبه می کنیم.

ابتدا ماتریس را به دو ماتریس جداگانه همانند مرحله 2 تقسیم می کنیم. سپس با میانگین گیری و محاسبه وزن ها مقدار لاندا را محاسبه می کنیم.
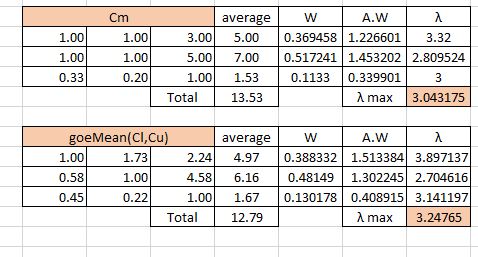
در گام نهایی ابتدا مقدار CI را محاسبه و با تقسیم آن بر مقدار تصادفی RI نرخ ناسازگاری مشخص می شود. اگر مقدار نهایی از 0.1 کمتر باشد ماتریس ما سازگار است.
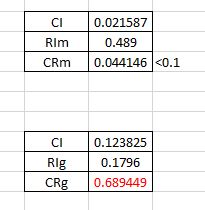
مشاهده می شود که مقدار CRg از 0.1 بیشتر است لذا توصیه می شود که مقایسهها از نو توسط خبرگان انجام شود.