آزمون µ با ∑ معلوم
- حالت یک متغیره H0: µ=µ0 با σ معلوم
فرضیه در اینجا این است که میانگین y برابر مقدار داده شده µ0 است یا خیر. شکل فرض صفر و فرض مقابل به صورت زیر است:
H1: µ ≠ µ0 H0: µ = µ0
در این آزمون ها یک نمونه تصادفی از n مشاهده y1,y2 تا yn از توزیع نرمال (N(µ,σ2 با معلوم بودن σ2 در نظر گرفته می شود.آزمون µ با ∑ معلوم
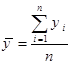
ابتدا بدست می آید و با استفاده از آماره آزمون زیر با µ0 مقایسه می شود.
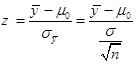
که دارای توزیع نرمال (N(0, 1 برای وقتی است که H0 درست باشد. اگر قدر مطلق Z یعنی Z|≥1.96| باشد فرض صفر رد می شود. این تصمیم گیری را می توان با Z2 دارای توزیع کای اسکور (X2) با درجه آزادی یک است. یعنی اگر = 3.84 2(≥(1.96 Z2)باشد، فرض H0 رد می شود.
- حالت چند متغیرهH0: µ=µ0 با ∑ معلوم
در حالت چند متغیره، چند متغیر از هر واحد نمونه گیری اندازه گیری شده است و ما می خواهیم برای میانگین هر متغیر یک مقدار را آزمون کنیم.

که در آن µoj یک مقدار معین از آزمایشات قبلی یا مقدار معین داده شده است. تساوی بردارها بدین معناست که در H0 برای کلیه j ها مقدار µoj= µj است و نامساوی H1 دلالت بر حداقل یکی از µoj≠ µj دارد.
برای آزمون فرض از یک نمونه تصادفی از بردار مشاهده n یعنی بردار y1,y2 تا yn از توزیع نرمال (N(µ,∑ با معلوم بودن ماتریس واریانس-کواریانس استفاده می کنیم.
بردار میانگین بدین صورت به دست می آید.
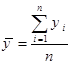
آماره آزمون به صورت زیر تعریف می شود:
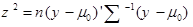
اگر H0 درست باشد، Z2 دارای توزیع (X2p) است یعنی اگر Z2 > X2α,pباشد فرض H0 را رد می کنیم. لازم به یادآوری است که برای یک متغیرZ2 دارای توزیع X2 با یک درجه آزادی است ولی برای P متغیر Z2 دارای توزیع X2 با P درجه آزادی می باشد.
نکته: اگر مقدار ∑ نامعلوم باشد، از S به جای ∑ استفاده می کنیم و در این حالت Z2 دارای توزیع تقریبی X2 خواهد بود اما مقدار n باید بزرگتر از حالت تک متغیره باشد. مقدار n لازم برای و داشتن توزیع X2 بستگی به P یعنی تعداد متغیرها دارد.
مثال: طول قد و وزن 20 دانشجو به شرح زیر است:
| دانشجو | قد(X) | وزن(Y) | دانشجو | قد(X) | وزن(Y) |
| 1 | 69 | 153 | 11 | 72 | 140 |
| 2 | 74 | 175 | 12 | 79 | 265 |
| 3 | 68 | 155 | 13 | 74 | 185 |
| 4 | 70 | 135 | 14 | 67 | 112 |
| 5 | 72 | 172 | 15 | 66 | 140 |
| 6 | 67 | 150 | 16 | 71 | 150 |
| 7 | 66 | 115 | 17 | 74 | 165 |
| 8 | 70 | 137 | 18 | 75 | 185 |
| 9 | 76 | 200 | 19 | 75 | 210 |
| 10 | 68 | 130 | 20 | 76 | 220 |
فرض کنید می خواهیم H0: µ=(70,170)’ را آزمون کنیم.
چند متغیره: فرض کنید: y1=71.45 و y2=164.7 است . در آن صورت خواهیم داشت:
با استفاده از α=0.05 مقدار X20.05,2=5.99 است. چون z2 = 8.4026>5.99 است لذا فرض H0: µ=(70,170) رد می شود
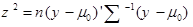
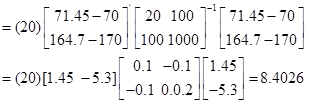
تک متغیره: خواهیم داشت اگر z α/2=1.96 و α=0.05 باشد در آن صورت می توان نوشت:
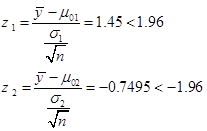
لذا هر دو آزمون شرط صفر را قبول می کنند. اما در روش چند متغیره چون همبستگی بین y1,y2 نیز به حساب می آید لذا سبب رد شدن فرض صفر می شود که همان قابلیت سوم آزمون فرض های چند متغیره است.
