آزمون µ با ∑ نامعلوم
- آزمون t یک متغیره H0: µ=µ0 با σ نامعلوم
در آزمون یک نمونه ای t فقط یک متغیر داریم که از هر واحد نمونه گیری بدست آمده است. فرض بر آن است که یک متغیر تصادفی y1,y2 تا yn از توزیع نرمال(N(µ,σ2 در دسترس است.
آزمون µ با ∑ نامعلوم
در اینجا µ را با Ӯ و σ2 را با S2 برآورد می کنیم و آزمون فرض به صورت H0: µ=µ0 و H1: µ≠µ0 است. از فرمول زیر استفاده می کنیم:
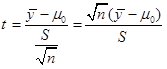
اگر t محاسبه شده از t α/2,n-1 بزرگتر یا مساوی آن باشد. فرض H0 را رد می کنیم. dF= n-1.
آزمون t2 هتلینگ چندمتغیره H0: µ=µ0 با ∑ نامعلوم
معمولا ∑ برای ما معلوم نیست، لذا باید از برآورد کننده نااُریب آن یعنی ماتریس S/n-1 استفاده کرد که در آن S ماتریس واریانس-کواریانس است. اگر ∑ معلوم نباشد توزیع µ دیگر توزیع نرمال چند متغیره نخواهد بود و لذا دیگر نمی توان از X2 برای محاسبه ناحیه اطمینان یا آزمون فرض درباره میانگین با مرکز جمعیت استفاده کرد.
در این حالت در موارد یک متغیره از شاخص آماری t به صورت زیر استفاده می شود:
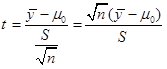
اگر آماره t را دوبرابر کنیم خواهیم داشت:
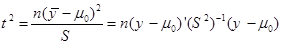
اگر به جای(µ0 – Ӯ) تک متغیره از (µ0 – Ӯ) چند متغیره و به جای S2 از ماتریس واریانس-کواریانسS استفاده کنیم خواهیم داشت:
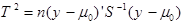
توزیع T2 دارای دو پارامتر است با ابعاد P تعداد متغیرها و dF=n-1 درجه آزادی. اگر α,P,n-1 T2> T2 محاسبه شده باشد فرض H0 رد می شود.
خصوصیات کلیدی T2 هتلینگ
- می بایستی n-1>p باشد در غیر این صورت S به صورت Singular بوده و نمی توان T2 را محاسبه نمود.
- در هر دو حالت تک و دو نمونه ای درجه آزادی T هتلینگ شبیه t یک متغیره است یعنی برای تک نمونه dF=n-1 و دو نمونه dF=n1+n2-1 خواهد بود.
- فرض مقابل دو دامنه است زیرا فضا چند بعدی است و لذا نمی توان آزمون یک دامنه را مورد توجه قرار داد.
- در حالت یک متغیره t2n-1 = F1,n-1 است. آماره T2 را نیز می توان به آماره F به صورت زیر تبدیل کرد.
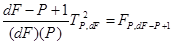
مثال: با استفاده از داده های ماتریس x فرض صفر =[7,11] µ H0:را با T2 در سطح 5 درصد ارزیابی کنید.
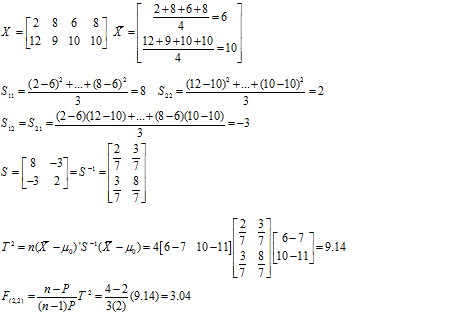
F جدول در سطح 5 درصد 19 است، لذا فرض صفر رد نمی شود.
