برنامه ریزی کسری خطی
برنامه ریزی کسری به عنوان یکی از فنون تحقیق در عملیات، یک ابزار مهم برنامه ریزی است که در زمینههای گوناگونی مثل تخصیص منابع، حمل و نقل، برنامهریزی تولید، ارزیابی عملکرد، مالی و غیره بکار گرفته شدهاست.
به این دلیل این نوع برنامه ریزی، کسری نامیده میشود که تابع هدف به صورت کسری و یا نسبت دو تابع است. این توابع میتوانند خطی و غیرخطی از متغیرهای تصمیم مسأله باشند.
به این نوع از مسائل برنامهریزی، برنامه ریزی کسری خطی (Linear Fractional Programming) گفته میشود.
شکل عمومی یک برنامه ریزی کسری به صورت زیر است:
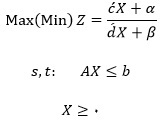
معادله عمومی برنامه ریزی خطی کسری
مسائل برنامه ریزی کسری خطی وقتی مطرح میشوند که نیازی به بهینهسازی کارایی چند فعالیت، سود بدست آمده
بوسیله شرکت به ازای هر واحد هزینه نیروی انسانی، هزینه تولید هر واحد کالای تولید شده، کالری رژیم غذایی به ازای هر واحد هزینه و غیره شکل بگیرد.
برنامه ریزی کسری
امروزه به دلیل کمبود منابع طبیعی استفاده از معیارهای خاص بیشتر از گذشته مطرح است.
بنابراین یکی از کاربردهای برنامهریزی کسری خطی برای حل مسائل واقعی با بهینه سازی کارایی پیوند خوردهاست.
با توجه به اینکه بسیاری از مدلهای دنیای واقعی نمیتواند در قالب مدلهای خطی تبیین شود، برنامه ریزی کسری یک شاخه از برنامه ریزی غیرخطی است که در دهه ۶۰ میلادی توسط توسعه داده شد
و برای مسائلی که تابع هدف آن بصورت یک کسر تعریف میشود، خیلی مناسب است.
برای حل این مدل برنامه ریزی ها از روش های مختلفی استفاده می شود که معروف ترین آن روش چارنز و کوپر است که در سال 1962 این روش را ابداع نموده اند.
روش چارنز و کوپر
اکنون ما روش دیگری را با استفاده از روش سیمپلکس برای حل مسئله برنامه ریزی کسری توصیف می کنیم.
مساله زیر را در نظر بگیرید.
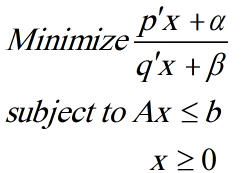
فرض کنید مجموعه
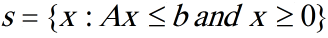
برنامه ریزی کسری
فشرده باشد و فرض کنید q’x + B> 0 برای هر x زیر مجموعه S باشد.
این به این ترتیب مجموعه های z و z به این صورت تعریف می شود.
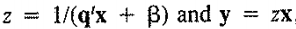
از این رو مساله برنامه ریزی خطی اول به صورت زیر تغییر پیدا می کند.
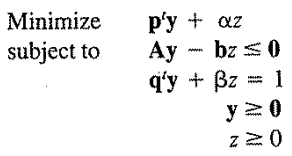
ابتدا توجه داشته باشید که اگر (y ، z) یک راه حل عملی برای مسئله فوق است z> 0 است.
این نتیجه می شود زیرا ، اگر z = 0 ، y! = 0 باید به گونه ای باشد که Ay <= 0 و y> = 0 ، به این معنی که y جهت S است ، فرض فشردگی را نقض می کند.
اکنون نشان می دهیم که اگر ( y ، z) یک راه حل بهینه برای برنامه خطی فوق است ،
سپس x = y / z یک راه حل بهینه برای برنامه کسری است.
برنامه ریزی کسری
توجه داشته باشید که Ax<=b و مقدار x>0 یک راه حل عملی برای برنامه کسری است. برای نشان دادن بهینه بودن x ، بگذارید x به گونه ای باشد که Ax<=b و x>=0.
توجه داشته باشید با فرضq’x + B> 0 و اینکه بردار (y ، z) یک راه حل عملی برای برنامه خطی است،
می توان مقادیر z و y را به صورت y = x / q’x + B و z = 1 / q’x + B تعیین کرد.
از آنجایی که بردار (y,z) یک راه حل عملی برای برنامه خطی است پس
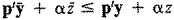
خواهد بود. باجایگزینی y ، y متوسط و z ، این عدم تناسب ایجاد می شود:
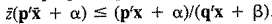
نتیجه بلافاصله با تقسیم سمت چپ بر 1 = q’y + Bz دنبال می شود.
حال ، اگر q’x + B <0 برای x <s ، پس z = 1 / q’x + b- و y = zx برنامه خطی زیر را ارائه می دهد:
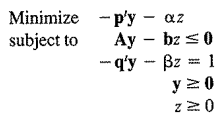
به روشی مشابه حالت بالا ، اگر (y ، z) برنامه خطی فوق را حل کند، x = y / z مسئله برنامه ریزی کسری را حل می کند.
برنامه ریزی کسری خطی
به طور خلاصه ، ما نشان داده ایم که برنامه ریزی کسری خطی را می توان با یک مسئله برنامه ریزی خطی با
یک متغیر اضافی و یک محدودیت اضافی حل کرد.
فرم برنامه خطی مورد استفاده به qx + B> 0 برای همه x <s یا q’x + B <0 برای همه x <s بستگی دارد.
پس اگر x1 یا x2 وجود داشته باشد به گونه ای که q’x1 + b> 0 ویا q’x2 + b <0 وجود داشته باشد ، راه حل بهینه برنامه کسری نامحدود است.
