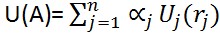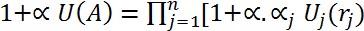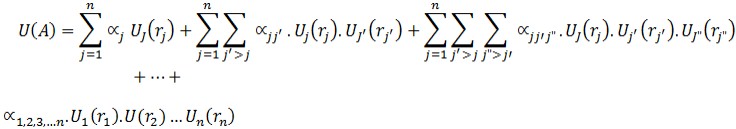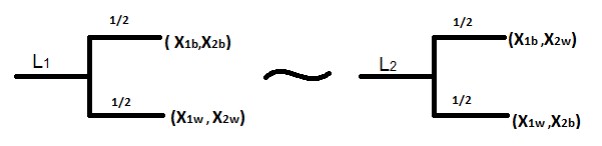تابع مطلوبیت در معنی ((رضایت خاطری که از مصرف کالاها و خدمات نصیب مصرف کننده می گردد)). مطلوبیت ابتدا در فلسفه به کار گرفته شد، بنتهام آن را به معنی میل به ایجاد نفع بکار برد و استوارت میل این اصطلاح را در رفتارهای انسانی مطرح کرد بطوری که به مطلوبیت گرایان شهرت یافتند. با انتشار کتاب جونز (1873) نظریه بنتهام وارد اقتصاد شد و همچنین توسط مورگن اشترن (1995) به عنوان وسیله ای برای سنجش نتیجه حاصل از تصمیم به کار گرفته شد.
تابع مطلوبیت تابع مطلوبیت تابع مطلوبیت تابع مطلوبیت تابع مطلوبیت
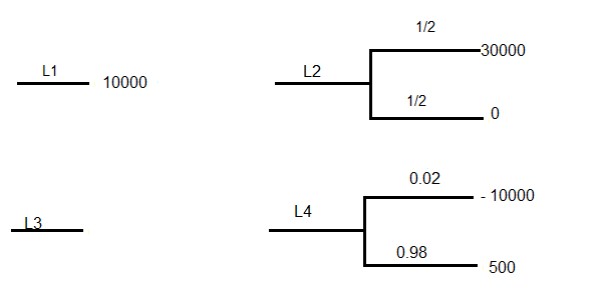
تعیین میزان مطلوبیت افراد برای کمک به تصمیم گیری در شرایط عدم اطمینان نیومن و اشترن برای رتبه بندی قرعه ها از مطلوبترین و بدترین نتیجه حاصل از قرعه ها استفاده کردند به عنوان مثال اگر چهار قرعه زیر را با احتمالات مختلف با توجه به نظر (DM) داشته باشیم می توان به ترتیب رتبه بندی کرد:
تابع مطلوبیت
(L3 < L4 < L2 < L1)
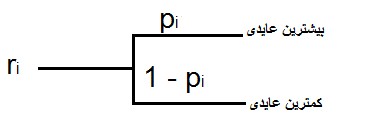
تعیین مطلوبیت پولی: مطلوبیت عایدی ri را به صورت u(ri) نوشته می شود و مقدار pi در دو قرعه زیر بگونه ای تعیین می شود که بین این دو بی تفاوتی حاکم شود.
بیشترین عایدی با مطلوبیت یک و کمترین عایدی با مطلوبیت صفر و برای هر قرعه داریم
(EU=∑PIU(Ri
آکسیوم های مطلوبیت : در جهت ترجیحات شخصی DM
- سه گانگی: برای هر دو عایدیr1 و r2 یکی از موارد زیر درست است:DM یا r1 را به r2 یاr2 را به r1 و یا بی تفاوت به هر دو است.
- انتقال پذیری: اگر شخصی r1 را به r2 و r2 را به r3 ترجیح دهد آنگاه r1 را به r3 ترجیح می دهد.
- پیوستگی: اگر تصمیم گیرنده r1 را به r2 و r2 را به r3 ترجیح دهد، آنگاه برای بعضی ازP ها (1> P> 0)L2 ~ L1 است.
- استقلال: اگر تصمیم گیرنده بین r1 و r2 بی تفاوت باشد و r3 عایدی دیگری باشد آنگاه برای (1> P> 0) L2 ~ L1
- احتمال نابرابر: اگر نتایج دو قرعهr1 و r2 باشد قرعه ای ترجیح داده می شود که دارای احتمال کسب عایدی بیشتری باشد.
تابع مطلوبیت چند شاخصه
هنگامیکه بیش از یک شاخص در ترجیحات موثر باشد آقایان raiffa&keeney (1976) معروفترین روش عملی برآورد از تابع مطلوبیت را پیشنهاد میدهند. روش آنان بر اساس تجزیه مساله به شاخصهای تشکیل دهنده آن بود و تعیین یک تابع مطلوبیت شرطی برای هر شاخص که این توابع شرطی به وسیله یکی از فرمهای زیر با یکدیگر ترکیب می شوند:
فرم جمع پذیر: (برای استفاده از آن احتیاج به شرط استقلال جمع پذیر داریم)
فرم حاصلضرب: (برای استفاده از آن احتیاج به شرط استقلال مطلوبیت متقابل داریم)
فرم ترکیبهای خطی چند گانه: (برای استفاده از آن فقط احتیاج به استقلال مطلوبیت داریم)
به طوری که (uj (rj بین صفر و یک خواهد بود و (UJ (rj یک تابع مطلوبیت شرطی است چنانچه:
- Uj (rj0)=0 به ازای ارزشی همچون rj0
- UJ(r*j)=1 به ازای ارزشی همچون r*j
خواص تابع مطلوبیت چند شاخصه
استقلال ترجیحی: شاخص x1 از شاخص x2 مستقل ترجیحی است اگر ترجیحات برای مقادیر شاخص اول به مقادیر شاخص دوم بستگی نداشته باشد.
استقلال ترجیحی دو به دو: شاخص x1 از شاخص x2 مستقل ترجیحی است اگر ترجیحات برای مقادیر شاخص اول به مقادیر شاخص دوم بستگی نداشته باشد و بر عکس. دو شاخص x1 از x2 از سایر شاخصها مستقل ترجیحی است اگر درجه ترجیح پیامدهای در برگیرنده تغییرات مربوط به سطح x1 و x2 به سطحی ثابت از سایر شاخصها بستگی نداشته باشد.
استقلال مطلوبیت: شاخص x1 از شاخص x2 استقلال مطلوبیت دارد اگر ترجیحات برای قرعه ها در میزان متفاوتی از سطح شاخص اول به مقادیر شاخص دوم بستگی نداشته باشد. استقلال مطلوبیت دو به دو: اگر x1 از x2 استقلال مطلوبیت داشته باشد و بالعکس
تابع مطلوبیت تابع مطلوبیت تابع مطلوبیت تابع مطلوبیت تابع مطلوبیت
U(X1,X2)=K1U1(X1)+ K2U2(X2) + K3U1(X1) U2(X2)
استقلال جمع پذیر: شاخصهای X1 ,X2,……Xn مستقل جمع پذیرند اگر درجه ترجیح برای پیشامدهای تصادفی به توزیع های احتمال مشترک آنها وابسته نبوده و تنها به توزیع احتمال حاشیه ای آن بستگی داشته باشد.برای دو شاخص مستقل جمع پذیر داریم:
U(X1,X2)=K1U1(X1)+ K2U2(X2)
گامهای لازم برای تعیین مطلوبیت چندگانه:
- بررسی استقلال مطلوبیت دو به دو اگر دارند به گام 2 اگر نه تعیین مطلوبیت چندگانه
- بررسی وضعیت استقلال جمع پذیر.
- محاسبه (U1(X1) و (U2(X2
- محاسبهK ها
- بررسی تابع مطلوبیت تعیین شده از نظر پیش بینی ترجیحات DM.
مثال تئوری تابع مطلوبت
مساله زیر را با استفاده از روش تابع مطلوبیت حل کنید:
Max f1(x) = 0.2 x1 + 0.7 x2
Max f2(x) = x2
s.to
2×1 + x2 <= 500
x1 + 2×2 <= 300
x1, x2 >=0
به منظور ارزیابی ترجیهات مدیریت شرکت دو مساله برنامه ریزی خطی زیر از طریق WINQSBحل می گردد:
مساله دوم مساله اول
Max f1(x) = 0.2 x1 + 0.7 x2 Max f2(x) = x2
s.to s.to
2×1 + x2 <= 500 2×1 + x2 <= 500
x1 + 2×2 <= 300 x1 + 2×2 <= 300
x1, x2 >=0 x1, x2 >=0
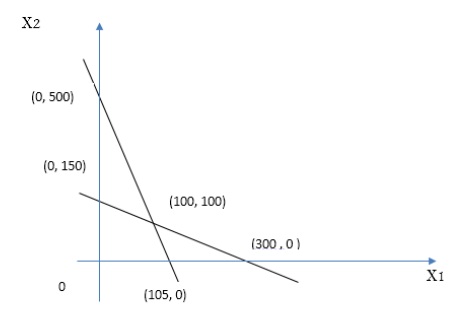
x1*=0 , x2*=150, z1*=105 x1*=0, x2*=150, z2*=150
بدین ترتیب ملاحظه می گردد:
0 <= Z1*<= 105
0<= Z2*<= 150
برای بدست آوردن (U1(z1,z2 مراحل زیر را انجام می دهیم:
گام اول:بررسی استقلال شاخص های z1 وz2:
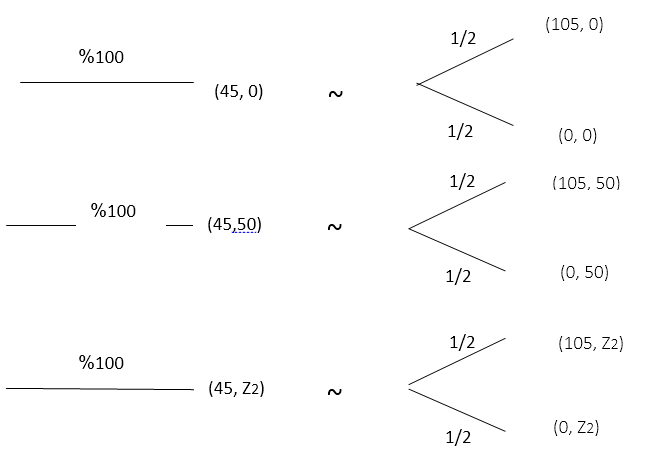
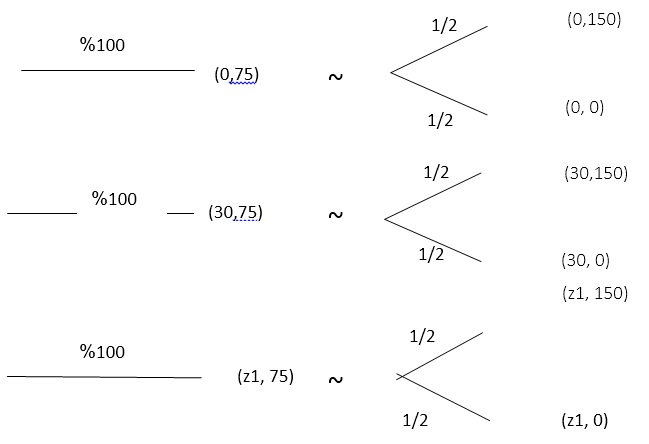
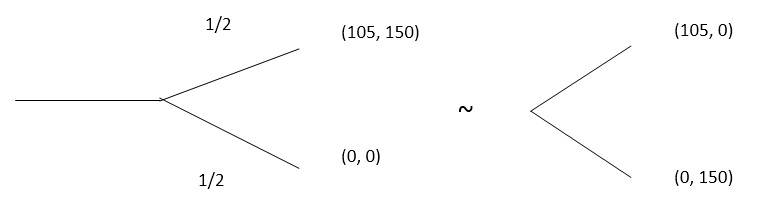
فرض می کنیم بازی های زیر برای تصمیم گیرنده دارای ارجحیت یکسان می باشند:
بررسی استقلال دو به دو شاخص ها:
بدین ترتیب مطلوبیت z1 از z2 مستقل است در صورتی که z2 نسبت به z1 نیز مستقل باشد می توان به گام بعدی رفت.
گام دوم : بررسی استقلال و جمع پذیری شاخص ها
گام سوم :محاسبه (u (z1 و (u (z2
ابتدا بازی های بی تفاوتی را با DM مطرح نموده و برای هر کدام از آن جهت دقت تابع مطلوبیت 10 نقطه در نظر می گیریم.
همچنین به طور دلخواه مبدا را بدین صورت در نظر می گیریم: u1(0,0)=0 u1(1,1)=0
برای z1 از عدد80 شروع می کنیم که فرضیهDM در بی تفاوتی است
اولویت محاسبه | U(z1) | Z1 |
0 | 0 | 0 |
8 | 50% u( 2 0) + 50% u(0)= 16.6 | 10 |
7 | 60% u( 40 )+ 40% u(0)=3 3.2 | 20 |
9 | 70% u( 4 0) +30% u( 2 0)= 48.6 | 30 |
6 | 70% u( 60 )+ 30% u(0)=5 5.4 | 40 |
2 | 60%u(105 )+40% u (0)=60 | 50 |
5 | 80% u( 70 ) +20% u( 50 )= 79.2 | 60 |
3 | 60% u(1 05 ) + 40% u( 50 )=8 4 | 70 |
4 | 90%u( 90 )+10%u( 50 )= 91.5 | 80 |
1 | 95% u(1 05 ) + 5% u (0) = 95 | 90 |
0 | 100 | 105 |
برای z2 از عدد 135 شروع می کنیم که فرضیه DM در بی تفاوتی است
اولویت محاسبه | U(z2) | Z2 |
0 | 0 | 0 |
8 | 50% u(30) + 50% u(0)=18 | 15 |
7 | 60% u(60)+ 40% u(0)=35 | 30 |
9 | 70% u(60) +30% u(30)=46 | 45 |
6 | 70% u(90)+ 30% u(0)=55 | 60 |
2 | 60%u(150 )+40% u (0)=60 | 75 |
5 | 80% u(105) +20% u(75)=78 | 90 |
3 | 60% u(135) + 40% u(75 )=82 | 105 |
4 | 90%u(135)+10%u(75)=88 | 120 |
1 | 95% u(150 ) + 5% u (0) = 95 | 135 |
0 | 100 | 150 |
با استفاده از نرم افزار Eviews تابع مطلوبیت را محاسبه می نماییم:
x1>=0 2x1+x2<=500
x2>=0 x1+2x2<=300
u1(f1)=a1(1-eb1f1) u2(f2)=a2(1-eb2f2)
a1=139.857 b1=-0.01263 a2=127.25 b2=-0.010167
u1 (z1) = 139.857(1-e–0.01263z1) u2 (z2) = 127.25 (1-e-0.010167z2)
تابع مطلوبیت تابع مطلوبیت تابع مطلوبیت تابع مطلوبیت تابع مطلوبیت
گام چهارم :تعیین مقادیر K1, K2, K3
فرض می کنیم DM مقادیر K1=0.7 و K2=0.6 را در نظر گرفته است لذا چون مجموع هر سه k باید برابر 1 گردد مقدار 0.3-=(K3 = (1-0.7-0.6 تعیین می گردد.
K2= 0.3 , 1- K2= 0.7
K3+K2+K1=1 K3= 1- K1+ K2 → → K3= 1- 0.6+ 0.3=0.1
U(z1,z2) = 0.7 u1(z1,0)+0.6 u2(z2,0)-0.3u3(z1,0)*u2(z2,0)
U (z1, z2) = 0.7 *(139.857(1-e–0.01263z1))+0.6(127.25 (1-e-0.010167z2))-0.3(139.857(1-e–0.01263z1)* 127.25 (1-e-0.010167z2)
گام پنجم: محاسبه مقدار U
حال با حل کرده معادله فوق و اعمال محدودیت ها x1 و x2 بهینه تابع را با استفاده از نرم افزار WINQSB بدست می آوریم:
U (x1, x2) = 0.7 *(139.857(1-e–0.01263×1)) + 0.6(127.25 (1-e-0.010167×2))-0.3(139.857(1-e–0.01263×1)* 127.25 (1-e-0.010167×2)
U (x1, x2) = -5164.79+5175.36 x+5209.46 y-5218.7 x y
S.to: 2X1 + X2≤ 500
X1 + 2 X2≤ 300
X1, X2 ≥ 0
X1* | X2* | F1(x*) | F2(x*) | U(x1,x2) |
250 | 0 | 50 | 0 | 5400 |
تصمیم گیری چند معیاره
تصمیمگیری شامل بیان درست اهداف، تعیین راهحلهای مختلف و ممکن، ارزیابی امکانپذیری آنان، ارزیابی عواقب و نتایج ناشی از اجرای هر یک از راهحلها و بالاخره انتخاب و اجرای آن میباشد. کیفیت مدیریت اساساً تابع کیفیت تصمیمگیری است زیرا کیفیت طرح و برنامهها، اثربخشی و کارآمدی راهبردها و کیفیت نتایجی که از اعمال آنها بدست میآید همگی تابع کیفیت تصمیماتی است که مدیر اتخاذ مینماید.
در اکثر موارد تصمیمگیریها وقتی مطلوب و مورد رضایت تصمیمگیرنده است که تصمیمگیری براساس چندین معیار مورد بررسی قرار گرفته باشد. معیارها ممکن است کمی یا کیفی باشند. در روشهای تصمیمگیری چند معیاره که در دهههای اخیر مورد توجه محققین قرار گرفتهاست به جای استفاده از یک معیار سنجش بهینگی از چند معیار سنجش استفاده میشود.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تص
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.