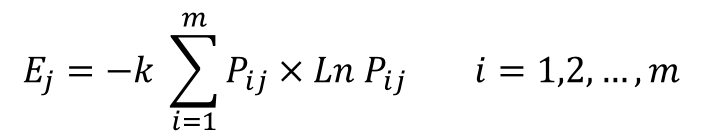روش آنتروپی شانون
در مسائل تصميم گيري چند معياره و بخصوص مسائل تصميم گيري چند شاخصه، داشتن و دانستن اوزان نسبي شاخص هاي موجود، گام مؤثري در فرايند حل مسئله بوده و مورد نياز است.
از جمله روش هاي تعيين وزن هاي شاخص ها، مي توان به روش هاي استفاده از پاسخ خبرگان، روش لينمپ، روش كمترين مجذورات، تكنيك بردار ويژه، آنتروپي شانون، روش CRITIC و… اشاره كرد.
روش Shannon Entropy
معمولا به هر یک از شاخص ها یک وزن نسبت داده می شود. به طوری که مجموع وزن شاخص ها برابر ۱ باشد.
برای تعیین وزن شاخص ها نیز روش های گوناگونی وجود دارد که روش آنتروپی، روش Linmap، روش بردار ویژه و روش کمترین مربعات مهم ترین روش های تعیین وزن شاخص ها می باشند. در این جا روش آنتروپی شرح داده می شود.
روش آنتروپی (Entropy) یکی از روشهای تصمیم گیری چند معیاره برای محاسبه وزن معیارها می باشد. در این روش نیازمند به ماتریس معیار-گزینه می باشد.
روش آنتروپی شانون برای وزن دهی شاخص ها (معیارها)
این روش در سال 1974 توسط شانون و ویور ارائه شد آنتروپی بیان کننده مقدار عدم اطمینان در یک توزیع احتمال پیوسته است. ایده اصلی این روش آن است که هر چه پراکندگی در مقادیر یک شاخص بیشتر باشد آن شاخص از اهمیت بیشتری برخوردار است.
شانون نشان داد که وقایع با احتمال وقوع زیاد اطالعات کمتری در اختیار می گذارند و برعکس هرچقدر احتمال وقوع یک رخداد کمتر باشد، اطلاعات حاصل از آن بیشتر است.
با به دست آوردن اطلاعات جدید، درواقع عدم قطعیت ها کاهش یافته و ارزش اطلاعات جدید برابر با مقداری است که از عدم قطعیت کاسته شده است. درنتیجه عدم قطعیت و اطلاعات پارامترهایی وابسته به هم هستند.
پرسشنامه روش آنتروپی شانون نیز همانند ماتریس آن می باشد. گام های این روش مطابق زیر می باشد:
گام های روش آنتروپی شانون
از روش آنتروپي شانون به عنوان يكي از معروفترين روش هاي محاسبه اوزان شاخص ها استفاده شده است.
مفهوم آنتروپی شانون (شانون ، 1948) نقش مهمی در نظریه اطلاعات دارد. این مفهوم در زمینه های مختلف علمی ، از جمله فیزیک ، علوم اجتماعی و غیره توسعه یافته است.
در تئوری اطلاعات ، آنتروپی اندازه گیری مقدار اطلاعات مورد نیاز برای توصیف متغیر تصادفی است.
گام اول:
ابتدا ماتریس تصمیم را تشکیل می دهیم. برای تشکیل این ماتریس تصمیم کافیست اگر معیارها کیفی هستند از عبارات کلامی ارزیابی هر گزینه را نسبت به هر معیار بدست آوریم و اگر معیارها کمی هستند عدد واقعی آن ارزیابی را قرار دهیم.
در شکل زیر که ماتریس تصمیم می باشد ستون ها معیار و سطرهای گزینه ها هستند. به عنوان مثال درایه x12 امتیاز گزینه اول نسبت به معیار دوم است.
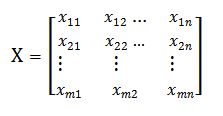
گام دوم:
ماتریس بالا را نرمال می کنیم و هر درایه نرمال شده را pij می نامیم. نرمال شدن به این صورت می باشد که
درایه هر ستون را بر مجموع ستون تقسیم می کنیم.
گام سوم:
محاسبه آنتروپی هر شاخص: آنتروپی Ej به صورت زیر محاسبه می گردد و k به عنوان مقدار ثابت مقدار Ej را
بین 0 و 1 نگه می دارد.
که در آن p (x) توزیع احتمال متغیر تصادفی X است. افزایش در آنتروپی شانون باعث افزایش عدم اطمینان و
کاهش اطلاعات در مورد دانش متغیر تصادفی می شود.
جنبه جالب دیگر آنتروپی شانون ویژگی حداکثر آنتروپی آن برای توزیع یکنواخت است.
روش آنتروپی شانون
گام چهارم:
در ادامه مقدار dj (درجه انحراف) محاسبه می شود که بیان می کند شاخص مربوطه (dj) چه میزان اطلاعات
مفید برای تصمیم گیری در اختیار تصمیم گیرنده قرار می دهد.
هر چه مقادیر اندازه گیری شده شاخصی به هم نزدیک باشند نشان دهنده آنست که گزینه های رقیب از نظر آن
شاخص تفاوت چندانی با یکدیگر ندارند.
dj=1-Ej
لذا نقش آن شاخص در تصمیم گیری باید به همان اندازه کاهش یابد.
گام پنجم:
سپس مقدار وزن Wj محاسبه می گردد. در واقع وزن معیار برابر با هر dj تقسیم بر مجموع dj ها می باشد.
wj=dj/∑dj
مثال روش آنتروپی شانون
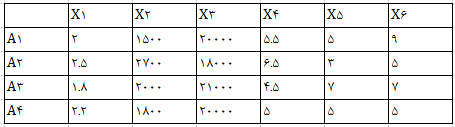
مثال:ماتریس تصمیم گیری زیر را با 4 گزینه و 6 معیار در نظر بگیرید:
روش آنتروپی شانون
Pij ها (ماتریس نرمال) به صورت زیر به دست می آیند:
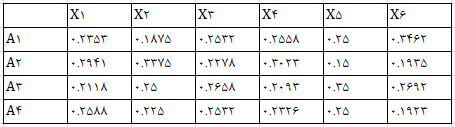
مقادیر Ej و dj و wj را بدست می آوریم.
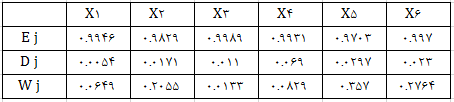
با توجه به جدول بالا
- وزن معیار اول 0.0649
- وزن معیار دوم 0.2055
- وزن معیار سوم 0.0133
- وزن معیار چهارم 0.0829
- وزن معیار پنجم 0.357 و
- وزن معیار ششم 0.2764 می باشد.