روش الکتره فازی
روش الکتره فازی
همان طور که در مسایل پیش روی خود در جهان هستی روبروه هستیم همواره داده های مساله به صورت مشخص نمی باشند، بلکه ممکن است به صورت فازی باشند. روش الکتری نیز برای حل این گونه مسایل دارای روش منحصر به خودش می باشد که با تغییراتی نسبت به حالت داده های قطعی در ادامه شرح داده خواهد شد.
روش الکتره با استفاده از داده های فازی:
ماتریس تصمیم فازی زیر را در نظر بگیرید.

گام اول: ماتریس تصمیم را به روش زیر نرمالایز می کنیم:
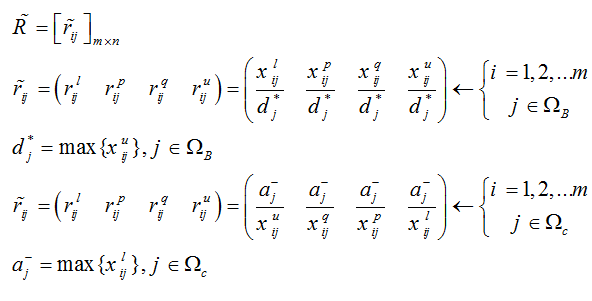
که به ترتیب شاخص های BΩ و CΩ مثبت و منفی می باشند.
گام دوم: در مرحله بعد بردار وزن را در ماتریس نرمالایز شده ضرب می کنیم تا ماتریس نرمالایز شده وزن دار بدست آید.
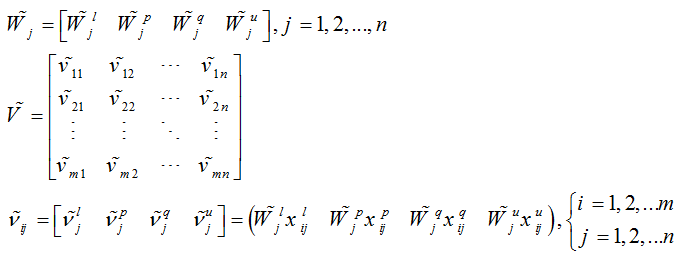
گاهی لازم است كه دو عدد فازی را با هم مقایسه كرده تا مشخص شود كه كدام یك بزرگ تر از دیگری است. گاهی نیز به دلیل متغیرهای زیاد و محاسبات گستردة اعداد فازی، باید اعداد فازی را به اعداد قطعی تبدیل كرد. به این كار دیفازی كردن )تبدیل اعداد از حالت فازی به قطعی( گفته می شود. مهم ترین روش های دیفازی كردن عبارتند از:
- روش میانگین
- روش مركز ناحیه
- روش برش α
- گشتاورها
فرمول روش میانگین برای اعداد ذوزنقه ای:
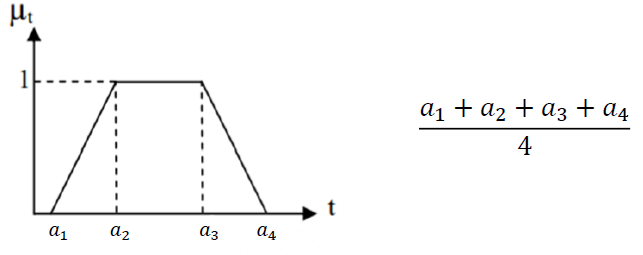
پس به منظور مقایسه گزینه ها و تعیین برتری اعداد را می توان دیفازی نمود.
گام سوم: اکنون باید مجموعه هماهنگ و ناهماهنگ را مشخص می کنیم.
با توجه به دو آلترناتیو Af و Ag مجموعه هماهنگ به صورت {Jc={ j|Vgi≥ Vfj تعریف می شودکه در آن Jc شامل اندیس معیارهایی است که درآن Ag بر Af ارجحیت دارد. زمانی Vgi≥ Vfj است که اگر و تنها اگر (d(Max (Vgi, Vfj), Vfj) ≥ d(Max (Vgi, Vfj), Vgi باشد.
همچنین زمانی اندیس معیاری در مجموعه ناهماهنگ جای می گیرد که:
JD= {j|Vgi≤ Vfj}
و زمانی Vgi≤ Vfj است که اگر و تنها اگر ((Max (Vgi, Vfj), Vfj) ≤ d(Max (Vgi, Vfj), Vgi) باشد. ماتریس هماهنگ به صورت زیر مشخص می شود:
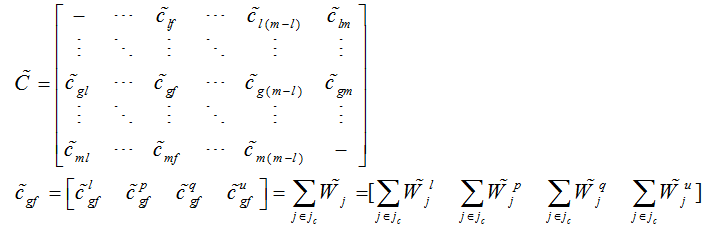
به عبارت دیگر عناصر ماتریس هماهنگ از جمع وزن فازی معیارهایی بدست می آیند که در مجموعه هماهنگ موجود هستند. ماتریس ناهماهنگ نیز به این صورت محاسبه می شود.
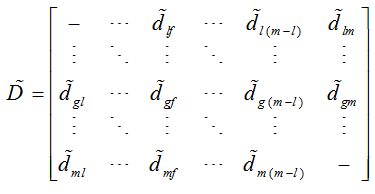
در این بخش اگر قصد نداشته باشیم از روش میانگین و یا سایر روش های ذکر شده در فوق استفاده نماییم می توانیم با توجه به مقاله ارائه شده توسط حاتمی و همکاران در سال 2011، فاصله ی بین دو آلترناتیو (d) را توسط فاصله ی همینگ بسنجیم.
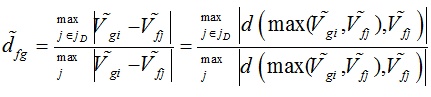
گام چهارم: حال باید آستانه ای برای ماتریس های هماهنگ و ناهماهنگ بدست آوریم.
مقدار آستانه ماتریس هماهنگ Č را می توان با میانگین گرفتن از عناصر ماتریس هماهنگ بدست آورد.
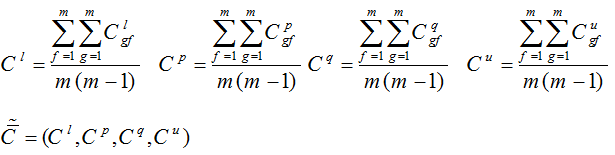
ماتریس B باتوجه به آستانه ماتریس هماهنگ Č بدین صورت بدست می آید:
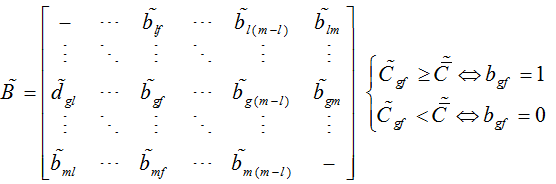
آستانه برای ماتریس ناهماهنگ (D):
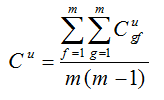
ماتریس H به صورت زیر محاسبه می گردد:
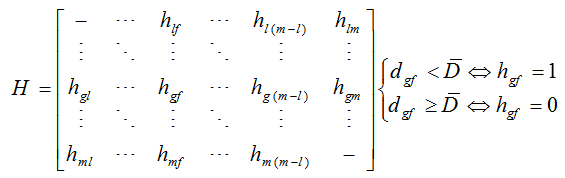
ماتریس کلی به صورت زیر بدست می آید:
Z=B*H
حال با توجه به ماتریس کلی بدست آمده، همانند روش الکتری با داده های قطعی رتبه بندی خواهیم کرد.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چند معیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.
