روش تخصیص خطی (LAM)
تکنیک تخصیص خطی (Linear Assignment Method) از روشهای تصمیم گیری چند معیاره است که توسط هانگ در سال 1983 ارائه شد و سپس توسط آکگول در سال 1993 توسعه داده شد.
هدف این تکنیک رتبه بندی گزینه های پژوهش است در این روش یک مساله تصمیم گیری چند شاخصه; را در قالب مدل برنامه ریزی خطی فرموله می کنیم.
این روش با استفاد از یک رتبه بندی ساده برای گزینه ها باعث می شود که از محاسبات پیچیده ;و وقت گیر خودداری شود. همچنین در این روش نیازی به نرمال سازی و یا یکسان سازی مقیاس ها نیست; و معیارها می توانند از هر مقیاسی باشد.
روش تخصیص خطی همچنین در زمره روشهای جبرانی قرار می گیرد;در مقایسه با سایر روشهای تصمیم گیری چندشاخصه و از جمله نقاط قوت و حائز اهمیت روش تخصیص خطی; این است که این روش از جمله فنون ترکیبی (سخت و نرم) محسوب می شود; فنون تصمیم گیری سخت به فنونی اطلاق می شود که تعریف مدل بر اساس دستگاه معادلات ریاضی انجام گیرد.
فنون تصمیم گیری نرم
فنون تصمیم گیری نرم فنونی هستند که در آن مدل بر مبنای یک جدول توافقی بیان می شود; لذا فنون تصمیم گیری ترکیبی از ترکیب فنون سخت و فنون نرم شکل می گیرند; به این معنی که این فنون ظاهراً از منطق فنون نرم پیروی می کنند ;و بر اساس جدول توافقی تعریف می شود ولی در عمل و فرایند حل; از دستگاه معادلات ریاضی بهره می گیرند لذا نقاط قوت فنون نرم و سخت را دارا هستند.
در روش تخصـــیص خطـــی، گزینـــه هـــای مســـئلة تصمیم گیـری چنـدمعیاره بـر مبنـای عملكـرد; هـر گزینـه برحسب هریك از معیارها رتبه بنـدی مـی شـود و درنهایـت رتبه بندی نهایی گزینه ها; از طریق فراینـد جبرانـی خطـی برای تركیب و تعامل معیارها به دسـت مـی آیـد.
در فراینـد جبران خطی فقـط داده هـای اُردینـال بـه عنـوان داده هـای ورودی استفاده می شوند بنابراین، به تبدیل داده های كیفی به كمی یا نرمال سازی داده ها نیازی نیست.
گام های روش تخصیص خطی
در اولین گام باید ماتریس تصمیم این روش را تشکیل داد ماتریس تصمیم ;روش تخصیص خطی یک ماتریس معیار گزینه است ;یعنی ماتریسی که ستون های آن را معیارها و سطرهای آن را گزینه های پژوهش تشکیل می دهد.
همچنین باید وزن معیارها را نیز با استفاده از روش های دیگر محاسبه کرد; و وارد این تکنیک نمود. فرض کنید وزن معیارها به ترتیب 0.1 و 0.4 و 0.5 باشد.
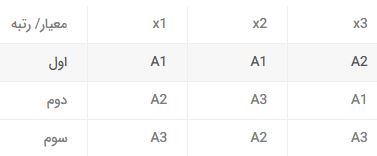
در گام بعد فراوانی رتبه هر گزینه را مشخص می کنیم:
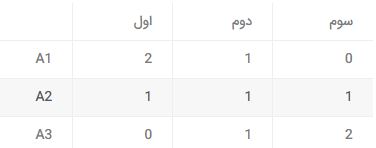
سپس بر اساس فراوانی اوزان معادل قرار می گیرد
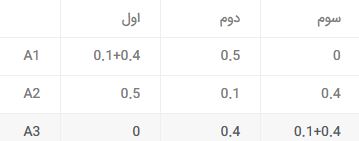
در این گام با استفاده از مدل برنامه ریزی خطی و حل آن رتبه بندی گزینه ها حاصل می شود. به مدل زیر برنامه ریزی صفر و یک گفته می شود;زیر جواب های این مدل تنها اعداد صفر و یک هستند که نشانه تخصیص یا عدم تخصیص هستند.

مثال روش تخصیص خطی (LAM)
به عنوان مثال انتخاب یک سیستم رایانه ای از بین سه سیستم موجود را در نظر می گیریم. وزن ها با توجه به روش آنتروپی شانون به دست آمده اند. W= (0.284, 0.178, 0.717, 0.246, 0.2203)
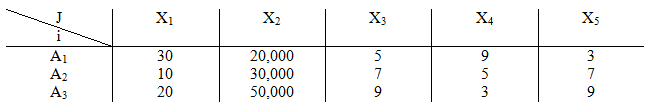
مرحله 1:
ماتریس تشکیل دهید که سطر های آن بیانگر رتبه ها و ستون های آن بیانگر شاخص ها باشد. با توجه به رتبه هر گزینه در هر شاخص، مولفه های ماتریس را با Ai پر کنید. این مرحله رتبه بندی گزینه ها نامیده می شود.
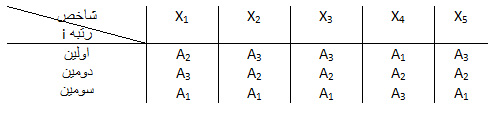
مرحله 2:
ماتریس rm×m را با توجه به بردار مفروض w استخراج کنید. عناصر این ماتریس که سطر های آن گزینه و ستون های آن رتبه می باشد، از مجموع وزن هایی به دست می آید که آن گزینه با توجه به آن شاخص حاصل کرده است. در مثال بیان شده ماتریس ϒ که یک ماتریس 3×3 است عبارت است از:
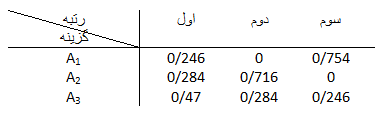
به عنوان نمونه 1و1وϒ از مجموع وزن شاخص هایی به دست می آید که گزینه A1 از نظر آن شاخص ها رتبه اول را کسب کرده باشد. گزینه A1 تنها از نظر شاخص چهارم، رتبه اول را کسب کرده و میزان آن برابر است با:
1و1وϒ=W4=0.246
و همچنین برای 3و1وϒ داریم:
3و1وϒ =W1+W2+W3+W5=0.285+0.0717+0.2203=0.754
مرحله 3:
بر اساس ماتریس به دست آمده از مرحله 2، جواب بهینه را استخراج کنید. این ماتریس به کمک هر یک از روش های حمل و نقل یا برنامه ریزی صفر و یک قابل استخراج است. در مدل ما جواب بهینه مشخص است.

پس از حل مدل رتبه بندی گزینه ها به صورت A3>A2>A1 خواهد بود.
