روش سکانت (Secant Method) که به نام روش خطوط نیز شناخته میشود، یک روش عددی برای یافتن ریشه معادلات غیرخطی تک متغیره است. این روش از دو نقطه دلخواه روی نمودار تابع شروع میشود و از طریق خطوطی که این نقاط را به هم متصل میکنند، به ریشه معادله نزدیک میشود.
این روش اولین بار در قرن شانزدهم توسط ریاضیدان ایتالیایی، تارtaglia، ابداع شد. اما تا قرن نوزدهم و توسط Lagrange به طور کامل مورد تجزیه و تحلیل قرار نگرفت.
ایده اصلی روش سکانت
ایده اصلی روش بر پایه یافتن تقاطع خطوط متصل کننده ی دو نقطه ی دلخواه روی نمودار تابع استوار است. این نقاط به طور تصادفی یا با استفاده از روش های دیگر مانند روش نیوتن-رافسون انتخاب می شوند.
همان طور که می دانیم روش نیوتن برای به حداقل رساندن تابع f از مشتق دوم تابع استفاده می نماید. حال اگر مشتق دوم در دسترس نباشد، ممکن است تلاش کنیم تا برای تخمین آن از اطلاعات مشتق اول استفاده نماییم. به طور خاص، ممکن است ما تقریبی از تابع f”(x) را از طریق زیر محاسبه نماییم:
f'(x(k)) – f'(x(k-1)) / x(k) –x(k-1)
با استفاده از تقریب فوق از مشتق دوم، الگوریتم زیر را به دست آوریم که به آن روش سکانت گفته می شود.
x (k+1) = x (k) – [(x(k) –x(k-1) ) / f'(x(k)) – f'(x(k-1))] * f'(x(k))
توجه داشته باشید که الگوریتم ما نیاز به دو نقطه اولیه برای شروع دارد که ما آنها را (X(0 و (X(-1 نامگذاری می نماییم. این روش را می توان در قالب معادله زیر نشان داد:
x (k+1) = [f'(x(k)) x (k-1) – f'(x(k-1)) x (k)] / [f'(x(k)) – f'(x(k-1))]
مشاهده می نمایید که مانند روش نیوتن، روش سـکانت به طور مستقیم از مقدار ((f(x(k استفاده نمی نماید. در عوض، تلاش می کند مقدار مشتق اول تابع ‘f را به سمت صفر هدایت نماید. درواقع ، مانند روش نیوتن، می توان از روش سـکانت به عنوان یک الگوریتم برای حل معادلات به شکل g(x) =0 استفاده نمود. به طور خاص روش سـکانت برای یافتن معادلات به شکل g(x) =0 به صورت زیر خواهد بود:
x (k+1) = x (k) – [(x(k) –x(k-1) ) / g(x(k)) – g(x(k-1))] *g(x(k))
یا به طور مشابه:
x (k+1) = [g(x(k)) x (k-1) – g(x(k-1)) x (k)] / [g(x(k)) – g(x(k-1))]
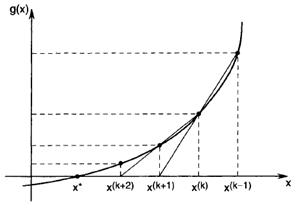
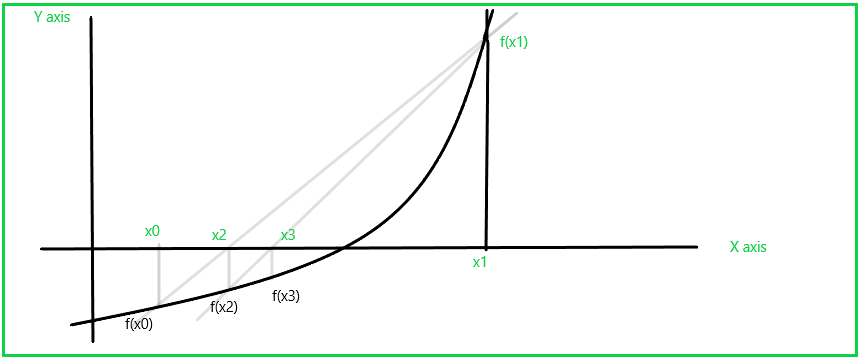
روش سـکانت برای پیدا کردن ریشه در شکل زیر نشان داده شده است. بر خلاف روش نیوتن، که از شیب g برای تعیین نقطه بعدی استفاده می نماید ، روش سکانت از ” خط قاطع” بین (k-1) امین و k امین نقطه برای تعیین (k+1) استفاده می نماید.
مراحل الگوریتم روش سکانت
الگوریتم روش سـکانت برای یافتن ریشه معادلات غیرخطی تک متغیره به شرح زیر است:
1. انتخاب نقاط اولیه:
- دو نقطه دلخواه
x_0وx_1را روی نمودار تابع انتخاب کنید. - می توانید از روش های مختلفی مانند حدس و خطا یا روش های عددی دیگر برای انتخاب نقاط اولیه استفاده کنید.
2. محاسبه نقطه تقاطع:
- نقطه تقاطع خطوط متصل کننده ی دو نقطه
x_0وx_1را محاسبه کنید. این نقطهx_2نامیده می شود. - می توانید از روش های مختلفی مانند روش خطی برای محاسبه نقطه تقاطع استفاده کنید.
3. محاسبه خطای تقریبی:
- خطای تقریبی
|x_2 - x_1|را محاسبه کنید.
4. بررسی شرایط همگرایی:
- اگر خطای تقریبی کمتر از مقدار مورد نظر (معمولاً
1e-6) باشد، فرآیند را متوقف کنید وx_2را به عنوان ریشه معادله در نظر بگیرید. - اگر خطای تقریبی بیشتر از مقدار مورد نظر باشد، به مرحله 5 بروید.
5. انتخاب دو نقطه جدید:
- اگر
f(x_2)وf(x_0)هم علامت باشند،x_0را باx_2جایگزین کنید. - اگر
f(x_2)وf(x_1)هم علامت باشند،x_1را باx_2جایگزین کنید.
6. بازگشت به مرحله 2:
- به مرحله 2 بازگردید و مراحل را تا زمانی که به شرایط همگرایی برسید، تکرار کنید.
نکات:
- انتخاب نقاط اولیه ی مناسب می تواند به سرعت همگرایی روش کمک کند.
- در برخی موارد ممکن است روش سکانت به ریشه ی معادله همگرا نشود.
- می توان از روش های مختلفی برای تسریع همگرایی روش سـکانت استفاده کرد.

مزایای روش سکانت
روش سـکانت (Secant Method) برای یافتن ریشه معادلات غیرخطی تک متغیره مزایای متعددی دارد که در ادامه به برخی از آنها اشاره میکنیم:
1. سادگی:
- این روش از نظر مفهومی و پیادهسازی بسیار ساده است.
- درک و استفاده از آن برای افراد مبتدی نیز آسان است.
2. عدم نیاز به مشتق:
- برخلاف روش نیوتن-رافسون، روش سـکانت نیازی به محاسبه مشتق تابع ندارد.
- این موضوع می تواند در مواردی که محاسبه مشتق دشوار یا غیرممکن است، مفید باشد.
3. پایداری:
- روش سکانت در مقایسه با روش نیوتن-رافسون از نظر عددی پایدارتر است.
- این موضوع به این معنی است که احتمال خطای عددی در این روش کمتر است.
4. کاربرد گسترده:
- روش سـکانت را می توان برای حل طیف وسیعی از معادلات غیرخطی تک متغیره به کار برد.
5. حافظه کم:
- روش سـکانت در مقایسه با روش نیوتن-رافسون به حافظه کمتری نیاز دارد.
- این موضوع می تواند در مواردی که حافظه محدود است، مفید باشد.
6. سرعت:
- در برخی موارد، روش سـکانت می تواند سریعتر از روش نیوتن-رافسون به ریشه معادله همگرا شود.
7. انعطاف پذیری:
- روش سکانت را می توان به راحتی با روش های دیگر مانند روش نیوتن-رافسون ترکیب کرد.
8. کاربرد در مسائل مهندسی:
- روش سکانت به طور گسترده در مسائل مهندسی مانند تحلیل سازه ها، طراحی سیستم ها و کنترل فرآیندها استفاده می شود.
9. کاربرد در علوم کامپیوتر:
- روش سکانت در علوم کامپیوتر در مسائلی مانند هوش مصنوعی، یادگیری ماشین و پردازش تصویر کاربرد دارد.
10. کاربرد در مسائل مالی:
- روش سکانت در مسائل مالی مانند تحلیل سهام، مدیریت ریسک و قیمت گذاری اوراق قرضه کاربرد دارد.
معایب روش سکانت
روش سکانت (Secant Method) برای یافتن ریشه معادلات غیرخطی تک متغیره، در کنار مزایای متعدد، معایبی نیز دارد که در ادامه به برخی از آنها اشاره میکنیم:
1. سرعت همگرایی:
- در برخی موارد، روش سکانت میتواند کندتر از روش نیوتن-رافسون باشد.
- به طور کلی، سرعت همگرایی روش سکانت مرتبه دوم است، در حالی که سرعت همگرایی روش نیوتن-رافسون مرتبه دوم یا مرتبه سوم است.
2. همگرایی:
- در برخی موارد، روش سکانت ممکن است به ریشه معادله همگرا نشود.
- این موضوع می تواند به دلیل انتخاب نقاط اولیه نامناسب یا رفتار تابع در نزدیکی ریشه باشد.
3. انتخاب نقاط اولیه:
- انتخاب نقاط اولیه مناسب می تواند به سرعت همگرایی روش کمک کند.
- با این حال، انتخاب نقاط اولیه مناسب همیشه آسان نیست و می تواند نیازمند دانش قبلی از تابع باشد.
4. حساسیت به خطاهای عددی:
- روش سکانت به خطاهای عددی حساس تر از روش نیوتن-رافسون است.
- این موضوع می تواند به دلیل استفاده از تفریق در فرمول محاسبه نقطه تقاطع خطوط باشد.
5. عدم وجود ضمانت برای وجود ریشه:
- روش سکانت هیچ ضمانتی برای وجود ریشه در بازه ی مورد نظر ارائه نمی دهد.
- در حالی که روش نیوتن-رافسون در صورت وجود ریشه در بازه ی مورد نظر، به طور همگرا به آن نزدیک می شود.
6. کاربرد محدود:
- روش سکانت برای حل معادلاتی که مشتق آنها به راحتی قابل محاسبه است، مناسب نیست.
- در این موارد، روش نیوتن-رافسون می تواند انتخاب بهتری باشد.
7. نیاز به حافظه بیشتر:
- روش سکانت در مقایسه با روش های دیگر مانند روش تنظیم خطی، به حافظه بیشتری نیاز دارد.
8. پیچیدگی پیاده سازی:
- پیاده سازی روش سکانت در مقایسه با روش های ساده تر مانند روش تنظیم خطی، پیچیده تر است.
کاربردهای روش سکانت
- مهندسی: در تحلیل سازه ها، از روش سکانت برای یافتن تنش و کرنش در سازه ها استفاده می شود.
- علوم کامپیوتر: در هوش مصنوعی، از روش سکانت برای یافتن ریشه معادلاتی که در آموزش شبکه های عصبی به کار می روند، استفاده می شود.
- مسائل مالی: در تحلیل سهام، از روش سکانت برای یافتن قیمت تعادلی سهام استفاده می شود.
- علوم پایه: در فیزیک، از روش سکانت برای یافتن ریشه معادلاتی که در شبیه سازی های فیزیکی به کار می روند، استفاده می شود.
- پزشکی: در تصویربرداری پزشکی، از روش سکانت برای بازسازی تصاویر پزشکی استفاده می شود.
انتخاب روش مناسب برای یافتن ریشه معادلات غیرخطی تک متغیره به عوامل مختلفی مانند نوع معادله، دقت مورد نظر و منابع محاسباتی موجود بستگی دارد.
از مشاوره با ما پشیمان نمی شوید
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.