
روش پرومته 2
در دنیای پیچیده امروز، انتخاب ایدهآلترین گزینه از میان انبوه گزینه ها، دغدغهای همیشگی برای انسان بوده است. در این میان، روشهای تصمیمگیری چندمعیاره (MADM) به عنوان ابزاری قدرتمند، یاریگر انسان در حل این چالش بزرگ هستند. روش پرومته 2 به عنوان یکی از روشهای نوین MADM، با رویکردی کارآمد و دقیق، به رتبهبندی و انتخاب بهترین گزینه کمک میکند.
آنچه می خوانید
روش پرومته 2 چیست
روش پرومته 2 در دهه 1980 توسط دو استاد بلژیکی به نامهای ژان پیر برنز و برتراند مارسکال ابداع شد. این روش در واقع تکامل یافته روش پرومته 1 است و با در نظر گرفتن ترجیحات و بیتفاوتیها، به رتبهبندی کامل گزینهها میپردازد.
اصول و مبانی
- شاخصها: معیارهایی که برای ارزیابی گزینهها به کار میروند.
- گزینهها: گزینه هایی که باید از بین آنها بهترین انتخاب شود.
- ترجیح: تمایل به انتخاب یک گزینه به جای گزینه دیگر.
- بیتفاوتی: عدم تمایل به انتخاب بین دو گزینه.
- آستانه بیتفاوتی: حداقل تفاوتی که بین دو گزینه باید وجود داشته باشد تا ترجیح ایجاد شود.
- آستانه ترجیح: حداقل تفاوتی که بین دو گزینه باید وجود داشته باشد تا ترجیح قوی ایجاد شود.
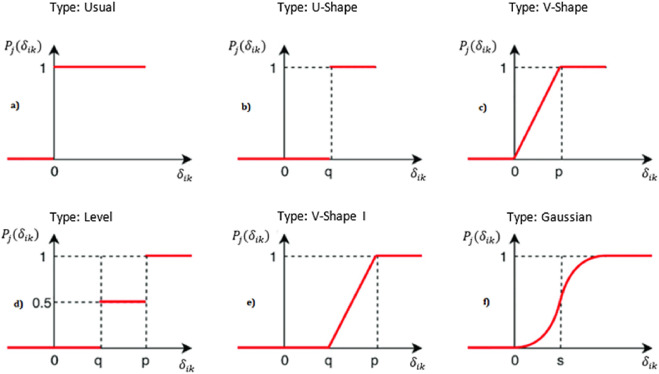
- تابع ترجیح: تابعی که میزان ترجیح یک گزینه به گزینه دیگر را نشان میدهد.
کاربردهای روش پرومته 2
روش پرومته 2 به عنوان ابزاری قدرتمند در تصمیمگیری چندمعیاره، در طیف وسیعی از مسائل و حوزهها کاربرد دارد. برخی از کاربردهای این روش عبارتند از:
انتخاب سبد سرمایهگذاری:
در این مسأله، سرمایهگذار باید از بین مجموعهای از اوراق بهادار، بهترین سبد سرمایهگذاری را با توجه به معیارهایی مانند ریسک، بازده، نقدشوندگی و … انتخاب کند. روش پرومته 2 میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای سرمایهگذار، به انتخاب ایدهآلترین سبد سرمایهگذاری کمک کند.
انتخاب پیمانکار:
در این مسأله، کارفرما باید از بین مجموعهای از پیمانکاران، بهترین پیمانکار را برای انجام یک پروژه با توجه به معیارهایی مانند قیمت، کیفیت، سابقه کار، زمانبندی و … انتخاب کند. روش پرومته 2 میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای کارفرما، به انتخاب ایدهآلترین پیمانکار کمک کند.
انتخاب محل احداث کارخانه:
در این مسأله، باید از بین مجموعهای از مکانهای مختلف، بهترین محل برای احداث یک کارخانه با توجه به معیارهایی مانند دسترسی به مواد اولیه، دسترسی به بازار، زیرساختها، هزینهها و … انتخاب شود. روش پرومته 2 میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای سرمایهگذار، به انتخاب ایدهآلترین محل برای احداث کارخانه کمک کند.
انتخاب طرحهای تحقیقاتی:
در این مسأله، باید از بین مجموعهای از طرحهای تحقیقاتی، بهترین طرحها با توجه به معیارهایی مانند نوآوری، اهمیت، امکانپذیری، هزینه و … انتخاب شود. روش پرومته 2 میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای تصمیمگیرندگان، به انتخاب ایدهآلترین طرحهای تحقیقاتی کمک کند.
انتخاب شغل:
در این مسأله، فرد باید از بین مجموعهای از شغلهای مختلف، بهترین شغل را با توجه به معیارهایی مانند حقوق، مزایا، علاقه، مهارت و … انتخاب کند. روش پرومته 2 میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای فرد، به انتخاب ایدهآلترین شغل کمک کند.
بیشتر بدانیم
انتخاب دانشگاه:
در این مسأله، فرد باید از بین مجموعهای از دانشگاههای مختلف، بهترین دانشگاه را با توجه به معیارهایی مانند رتبه، رشته تحصیلی، شهریه، امکانات و … انتخاب کند. روش پرومته 2 میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای فرد، به انتخاب ایدهآلترین دانشگاه کمک کند.
انتخاب خودرو:
در این مسأله، فرد باید از بین مجموعهای از خودروهای مختلف، بهترین خودرو را با توجه به معیارهایی مانند قیمت، مصرف سوخت، ایمنی، شتاب و … انتخاب کند. روش پرومته 2 میتواند با در نظر گرفتن ترجیحات و بیتفاوتیهای فرد، به انتخاب ایدهآلترین خودرو کمک کند.

علاوه بر موارد ذکر شده، روش پرومته 2 در زمینههای دیگری مانند انتخاب روش درمانی، انتخاب هتل، انتخاب رستوران و … نیز کاربرد دارد. انتخاب معیارهای مناسب و تعیین آستانههای بیتفاوتی و ترجیح، نقش مهمی در کارایی و دقت روش پرومته 2 دارد.
مزایای روش پرومته 2
- سادگی و سهولت استفاده
- کارایی در شرایط عدم قطعیت و اطلاعات ناقص
- توجه به ترجیحات و بیتفاوتیهای تصمیمگیرنده
- ارائه رتبهبندی کامل گزینهها
- قابلیت استفاده در طیف وسیعی از مسائل
معایب روش پرومته 2
- نیاز به محاسبات نسبتاً پیچیده
- عدم وجود ضمانت برای یافتن جواب ایدهآل در همه مسائل
- وابستگی نتایج به انتخاب تابع ترجیح
مراحل روش پرومته 2
- تعریف گزینهها و معیارها: در این مرحله، باید گزینهها و معیارهای مورد نظر برای انتخاب ایدهآلترین گزینه مشخص شوند.
- تشکیل ماتریس تصمیم: در این مرحله، باید امتیاز هر گزینه در هر معیار مشخص شود.
- تعیین آستانههای بیتفاوتی و ترجیح: در این مرحله، باید آستانههای بیتفاوتی و ترجیح برای هر معیار مشخص شود.
- محاسبه ماتریس جریان ورودی و خروجی: در این مرحله، ماتریسهای جریان ورودی و خروجی با توجه به ترجیحات و بیتفاوتیها محاسبه میشوند.
- محاسبه شاخص پرومته: در این مرحله، شاخص پرومته برای هر گزینه محاسبه میشود.
- رتبهبندی گزینهها: در این مرحله، گزینهها بر اساس شاخص پرومته رتبهبندی میشوند.
محدودیتهای روش پرومته 2
- این روش برای حل مسائل با تعداد زیادی گزینه مناسب نیست.
- این روش برای حل مسائل با معیارهای کیفی نامناسب است.
نرمافزارهای مرتبط
- Visual PROMETHEE
- Promethee GAIA
- Decision Lab
الگوریتم حل روش پرومته 2
گام اول: تعریف مسئله و شناسایی گزینه ها
- در این مرحله، مسئله مورد نظر به طور کامل تعریف شده و گزینه های مختلف برای انتخاب مشخص می شوند.
- به عنوان مثال، می خواهیم از بین 3 خودرو A، B و C با توجه به 4 معیار قیمت، سرعت، مصرف سوخت و ایمنی، بهترین خودرو را انتخاب کنیم.
گام دوم:تعیین معیارها و شاخص ها
- معیارها، ویژگی های اصلی هستند که برای ارزیابی گزینه ها استفاده می شوند.
- شاخص ها، مقیاس های اندازه گیری هر معیار هستند.
- برای مثال، معیار قیمت می تواند با شاخص “قیمت نهایی” و معیار سرعت می تواند با شاخص “حداکثر سرعت” اندازه گیری شود.
گام سوم:تعیین ترجیحات و آستانه ها
- در این مرحله، ترجیحات تصمیم گیرنده برای هر معیار مشخص می شود.
- ترجیحات می تواند به صورت “بیشتر بهتر” یا “کمتر بهتر” باشد.
- آستانه های بیتفاوتی و ترجیح نیز برای هر معیار تعیین می شوند.
- آستانه بیتفاوتی، حداقل تفاوتی است که بین دو گزینه باید وجود داشته باشد تا ترجیح ایجاد شود.
- آستانه ترجیح، حداقل تفاوتی است که بین دو گزینه باید وجود داشته باشد تا ترجیح قوی ایجاد شود.
گام چهارم: محاسبه ماتریس ترجیحات
- ماتریس ترجیحات، نشان دهنده ترجیح هر گزینه نسبت به هر گزینه دیگر است.
- برای محاسبه ماتریس ترجیحات، از تابع ترجیح استفاده می شود.
- تابع ترجیح، تابعی است که میزان ترجیح یک گزینه به گزینه دیگر را نشان می دهد.
ماتریس ترجیحات نشان دهنده ترجیح هر گزینه نسبت به هر گزینه دیگر است. برای محاسبه ماتریس ترجیحات، از تابع ترجیح استفاده می شود. تابع ترجیح، تابعی است که میزان ترجیح یک گزینه به گزینه دیگر را نشان می دهد.
فرمول ماتریس ترجیحات:
P_{ij} = f(d_j - d_i)در این فرمول:
P_{ij}: ترجیح گزینهiنسبت به گزینهjf(.): تابع ترجیحd_i: مقدار شاخصiبرای گزینهin: تعداد گزینه ها
توابع ترجیح:
توابع ترجیح مختلفی وجود دارد که می توان از آنها در روش پرومته 2 استفاده کرد. برخی از رایج ترین توابع ترجیح عبارتند از:
- تابع ترجیح خطی:
f(x) = x
- تابع ترجیح گاوس:
f(x) = e^(-x^2/2σ^2)
- تابع ترجیح شبه خطی:
f(x) =
{
x, if x > q
0, if x <= q
}
در این فرمول:
σ: انحراف معیارq: آستانه بیتفاوتی
گام پنجم: محاسبه ماتریس جریان ورودی و خروجی
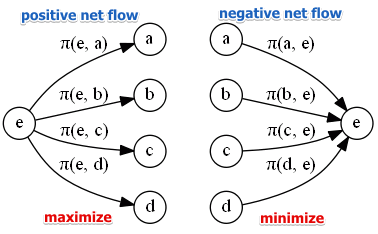
ماتریس جریان ورودی (Φ+) نشان میدهد که هر گزینه چقدر از سایر گزینهها ترجیح داده میشود. ماتریس جریان خروجی (Φ-) نشان میدهد که هر گزینه چقدر توسط سایر گزینهها ترجیح داده میشود.
Φ+ = 1/m[π(a,b)]
Φ- = 1/m[π(b,a)]گام ششم: محاسبه شاخصهای پرومته
شاخص پرومته I برای هر گزینه، تفاضل ماتریسهای جریان ورودی و خروجی آن گزینه است.
I(a) = Φ+(a) - Φ-(a)گام هفتم: رتبه بندی گزینه ها:
- گزینه ها بر اساس شاخص های Φ و Ψ رتبه بندی می شوند.
- به طور کلی، گزینه ای که بیشترین مقدار Φ و کمترین مقدار Ψ را داشته باشد، بهترین گزینه است.
مثال روش PROMETHEE II
فردی قصد دارد كه یكی از 4 مدل گوشی همراه سامسونگ، ال جی، سونی، اپل را خریداری كند. برای این گوشی ها 4 شاخص در نظر گرفته شده است. با روش پرومته 2 این رتبه بندی را انجام می دهیم.
| اوزان | 0.35 | 0.25 | 0.25 | 0.15 |
| نوع | منفی | مثبت | مثبت | مثبت |
| گزینه ها | قیمت | حافظه | دوربین | زیبایی |
| M1 | 250 | 16 | 12 | 5 |
| M2 | 200 | 16 | 8 | 3 |
| M3 | 300 | 32 | 16 | 4 |
| M4 | 275 | 32 | 8 | 2 |
گام اول: نرمال سازی ماتریس
برای از بین بردن اثر علامت شاخص ها ابتدا ماتریس را نرمال می کنیم. می توانیم از انواع روش های نرمال سازی نرم، اقلیدسی و غیره برای این منظور استفاده کنیم.
| ماتریس تصمیم گیری نرمال | ||||
| گزینه ها | قیمت | حافظه | دوربین | زیبایی |
| M1 | 0.50 | 0.00 | 0.50 | 1.00 |
| M2 | 1.00 | 0.00 | 0.00 | 0.33 |
| M3 | 0.00 | 1.00 | 1.00 | 0.67 |
| M4 | 0.25 | 1.00 | 0.00 | 0.00 |
گام دوم: محاسبه اختلاف بین گزینه ها
در این گام اختلاف هر یک از گزینه ها را با همدیگر محاسبه می کنیم.
| گزینه ها | قیمت | حافظه | دوربین | زیبایی |
| M1-M2 | -0.50 | 0.00 | 0.50 | 0.67 |
| M1-M3 | 0.50 | -1.00 | -0.50 | 0.33 |
| M1-M4 | 0.25 | -1.00 | 0.50 | 1.00 |
| M2-M1 | 0.50 | 0.00 | -0.50 | -0.67 |
| M2-M3 | 1.00 | -1.00 | -1.00 | -0.33 |
| M2-M4 | 0.75 | -1.00 | 0.00 | 0.33 |
| M3-M1 | -0.50 | 1.00 | 0.50 | -0.33 |
| M3-M2 | -1.00 | 1.00 | 1.00 | 0.33 |
| M3-M4 | -0.25 | 0.00 | 1.00 | 0.67 |
| M4-M1 | -0.25 | 1.00 | -0.50 | -1.00 |
| M4-M2 | -0.75 | 1.00 | 0.00 | -0.33 |
| M4-M3 | 0.25 | 0.00 | -1.00 | -0.67 |
گام سوم: محاسبه ترجحات بین گزینه
برای محاسبه ترجیحات، از انواع تابع ترجیح می توان استفاده کرد. در این مثال از تابع ترجیح عادی استفاده شده است.
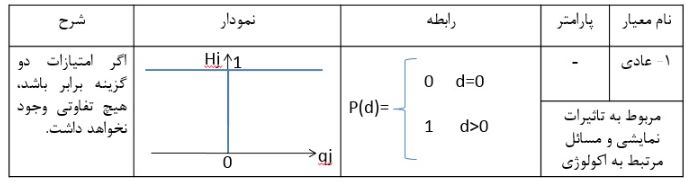
بدین معنی که گزینه هایی که اختلاف آنها کمتر یا مساوی صفر باشد مقدار صفر و سایر گزینه ها مقدار اختلاف را به خود اختصاص می دهند.
| اوزان | 0.35 | 0.25 | 0.25 | 0.15 |
| گزینه ها | قیمت | حافظه | دوربین | زیبایی |
| M1-M2 | 0.00 | 0.00 | 0.50 | 0.67 |
| M1-M3 | 0.50 | 0.00 | 0.00 | 0.33 |
| M1-M4 | 0.25 | 0.00 | 0.50 | 1.00 |
| M2-M1 | 0.50 | 0.00 | 0.00 | 0.00 |
| M2-M3 | 1.00 | 0.00 | 0.00 | 0.00 |
| M2-M4 | 0.75 | 0.00 | 0.00 | 0.33 |
| M3-M1 | 0.00 | 1.00 | 0.50 | 0.00 |
| M3-M2 | 0.00 | 1.00 | 1.00 | 0.33 |
| M3-M4 | 0.00 | 0.00 | 1.00 | 0.67 |
| M4-M1 | 0.00 | 1.00 | 0.00 | 0.00 |
| M4-M2 | 0.00 | 1.00 | 0.00 | 0.00 |
| M4-M3 | 0.25 | 0.00 | 0.00 | 0.00 |
گام چهارم: محاسبه ماتریس ترجیح وزن دار
در این گام اوزان هر یک از معیارها در مقدار ترجیح آن ضرب و ماتریس ترجیح وزن دار محاسبه می شود. در ادامه مقدار ترجیح وزن دار هر یک از اختلافات با هم جمع می شود
| گزینه ها | قیمت | حافظه | دوربین | زیبایی | SUM |
| M1-M2 | 0.000 | 0.000 | 0.125 | 0.100 | 0.2250 |
| M1-M3 | 0.175 | 0.000 | 0.000 | 0.050 | 0.2250 |
| M1-M4 | 0.088 | 0.000 | 0.125 | 0.150 | 0.3625 |
| M2-M1 | 0.175 | 0.000 | 0.000 | 0.000 | 0.1750 |
| M2-M3 | 0.350 | 0.000 | 0.000 | 0.000 | 0.3500 |
| M2-M4 | 0.263 | 0.000 | 0.000 | 0.050 | 0.3125 |
| M3-M1 | 0.000 | 0.250 | 0.125 | 0.000 | 0.3750 |
| M3-M2 | 0.000 | 0.250 | 0.250 | 0.050 | 0.5500 |
| M3-M4 | 0.000 | 0.000 | 0.250 | 0.100 | 0.3500 |
| M4-M1 | 0.000 | 0.250 | 0.000 | 0.000 | 0.2500 |
| M4-M2 | 0.000 | 0.250 | 0.000 | 0.000 | 0.2500 |
| M4-M3 | 0.088 | 0.000 | 0.000 | 0.000 | 0.0875 |
گام پنجم: محاسبه ماتریس جریان ورودی و خروجی
در ادامه با توجه به مجموع وزن های بدست آمده ماتریس ارتباط بین گزینه ها تشکیل می شود.
| گزینه ها | M1 | M2 | M3 | M4 | ф+ |
| M1 | 0.00 | 0.23 | 0.23 | 0.36 | 0.8125 |
| M2 | 0.18 | 0.00 | 0.35 | 0.31 | 0.8375 |
| M3 | 0.38 | 0.55 | 0.00 | 0.35 | 1.2750 |
| M4 | 0.25 | 0.25 | 0.09 | 0.00 | 0.5875 |
| ф- | 0.8000 | 1.0250 | 0.6625 | 1.0250 |
گام ششم: محاسبه شاخصهای پرومته
شاخص پرومته II برای هر گزینه، تفاضل ماتریسهای جریان ورودی و خروجی آن گزینه است.
| گزینه ها | ф+ | ф- | ф | رتبه بندی |
| M1 | 0.2708 | 0.2667 | 0.0042 | 2 |
| M2 | 0.2792 | 0.3417 | -0.0625 | 3 |
| M3 | 0.4250 | 0.2208 | 0.2042 | 1 |
| M4 | 0.1958 | 0.3417 | -0.1458 | 4 |
گام هفتم: رتبه بندی گزینه ها:
- گزینه ها بر اساس شاخص های Φ و Ψ رتبه بندی می شوند.
- به طور کلی، گزینه ای که بیشترین مقدار Φ و کمترین مقدار Ψ را داشته باشد، بهترین گزینه است.
مشاهده می شود که گزینه سوم بهترین گزینه و گزینه چهارم بدترین انتخاب است.
سوالات متداول
روشهای پرومته و پرومته 2 چه هستند؟
روشهای پرومته و پرومته 2 از جمله روشهای محبوب برای حل مسائل تصمیمگیری چندمعیاره هستند. این روشها به شما کمک میکنند تا با در نظر گرفتن ترجیحات و اولویتهای خود، بهترین گزینه را از بین گزینه های مختلف انتخاب کنید
تفاوت روشهای پرومته و پرومته 2 در چیست؟
روش پرومته روشی سادهتر است، اما روش پرومته 2 اطلاعات دقیقتری را در مورد ترجیحات شما ارائه میدهد. روش پرومته 2 از توابع ترجیح استفاده میکند، که انعطافپذیری بیشتری را برای شما فراهم میکند.
چه زمانی باید از روشهای پرومته و پرومته 2 استفاده کرد؟
از روشهای پرومته و پرومته 2 میتوان برای حل مسائل مختلفی مانند انتخاب سبد سرمایهگذاری، انتخاب پیمانکار، انتخاب محل احداث کارخانه، انتخاب طرحهای تحقیقاتی، انتخاب شغل و انتخاب خودرو استفاده کرد
چگونه میتوان از روشهای پرومته و پرومته 2 استفاده کرد؟
برای استفاده از روشهای پرومته و پرومته 2، باید مراحل زیر را انجام دهید:
معیارهای خود را تعریف کنید.
آستانههای بیتفاوتی و ترجیح خود را برای هر معیار تعیین کنید.
ماتریس تصمیم را تشکیل دهید.
ماتریس جریان ورودی و خروجی را محاسبه کنید.
شاخص پرومته را برای هر گزینه محاسبه کنید.
گزینهها را بر اساس شاخص پرومته رتبهبندی کنید.
چه نرمافزارهایی برای استفاده از روشهای پرومته و پرومته 2 وجود دارد؟
نرمافزارهای مختلفی برای استفاده از روشهای پرومته و پرومته 2 وجود دارد، مانند Visual PROMETHEE، Promethee GAIA و Decision Lab
مزایای استفاده از روشهای پرومته و پرومته 2 چیست؟
مزایای استفاده از روشهای پرومته و پرومته 2 عبارتند از:
سادگی و سهولت استفاده
انعطافپذیری
دقت
قابلیت استفاده برای حل مسائل مختلف
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.





