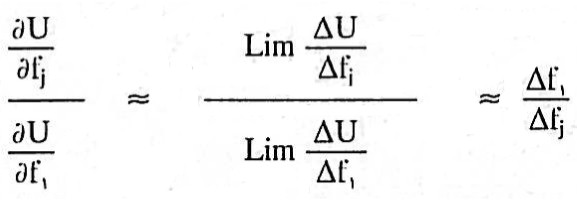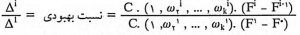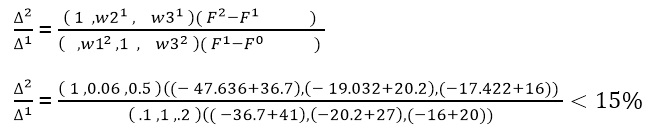روش گرادیان یک روش بهینه سازی است که برای یافتن کمینه یا بیشینه محلی یک تابع استفاده می شود. این روش بر اساس این اصل است که هر نقطه در فضای جستجو دارای یک گرادیان است که جهت افزایش سریعترین تابع را نشان می دهد. با حرکت به سمت مخالف گرادیان، به سمت کمینه یا بیشینه محلی حرکت می کنیم.
فهرست مطالب
روش گرادیان در حل مسائل چندهدفه به گفرین (Geoffrion) منتسب است. این روش قادر به حل مسائل بهینه سازی خطی و غیرخطی است به شرطی که خبره بتواند تابع مطلوبیت کلی خود را از اهداف مسئله مشخص نماید.
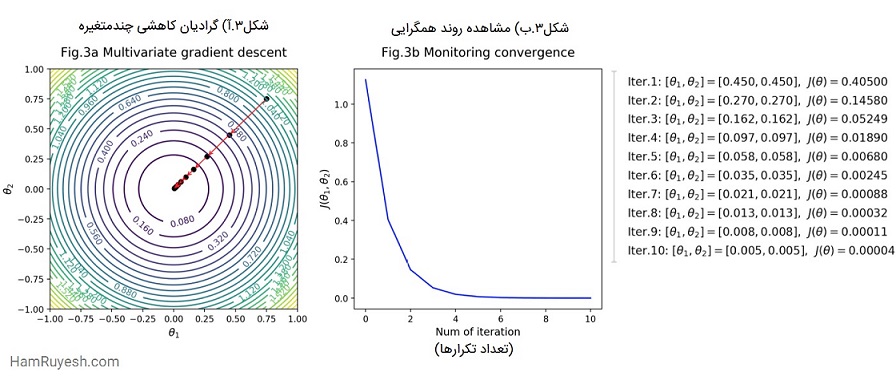
روش گرادیان یک روش ساده و موثر است که برای طیف گسترده ای از مسائل بهینه سازی استفاده می شود. با این حال، ممکن است در مواردی که تابع دارای چندین کمینه یا بیشینه محلی باشد، کارآمد نباشد.
مراحل روش گرادیان
گام های روش گرادیان به شرح زیر است:
- انتخاب نقطه اولیه
ابتدا باید یک نقطه اولیه در فضای جستجو انتخاب کنیم. این نقطه می تواند هر نقطه ای باشد که به نظر می رسد نزدیک به کمینه یا بیشینه محلی باشد. انتخاب نقطه اولیه یک مرحله مهم در روش گرادیان است. اگر نقطه اولیه بیش از حد دور از کمینه یا بیشینه محلی باشد، ممکن است روش گرادیان به آن نقطه نرسد.
در برخی از موارد، می توان از روش های مختلفی برای انتخاب نقطه اولیه استفاده کرد. به عنوان مثال، می توان از روش های زیر استفاده کرد:
- انتخاب نقطه ای به صورت تصادفی
- انتخاب نقطه ای در وسط فضای جستجو
- انتخاب نقطه ای که گرادیان آن صفر باشد
- محاسبه گرادیان
در مرحله بعدی، باید گرادیان تابع را در نقطه فعلی محاسبه کنیم. گرادیان یک بردار است که جهت افزایش سریعترین تابع را نشان می دهد. محاسبه گرادیان یک تابع می تواند دشوار باشد. با این حال، برای بسیاری از توابع، می توان گرادیان را به صورت تحلیلی محاسبه کرد. در برخی از موارد، نیز می توان از روش های عددی برای محاسبه گرادیان استفاده کرد.
- حرکت در جهت مخالف گرادیان
در مرحله سوم، باید در جهت مخالف گرادیان، یک قدم کوچک برداریم. این قدم کوچک به ما کمک می کند تا به سمت کمینه یا بیشینه محلی حرکت کنیم. اندازه قدم برداشته شده در جهت مخالف گرادیان، یک عامل مهم در روش گرادیان است.
اگر اندازه قدم بیش از حد بزرگ باشد، ممکن است روش گرادیان از کمینه یا بیشینه محلی خارج شود. اگر اندازه قدم بیش از حد کوچک باشد، ممکن است روش گرادیان به کندی به سمت کمینه یا بیشینه محلی حرکت کند.
در روش گرادیان ساده، اندازه قدم معمولا ثابت است. در روش گرادیان کاهش وزن، اندازه قدم به تدریج کاهش می یابد. این به جلوگیری از پرش از کمینه یا بیشینه محلی کمک می کند.
- تکرار مراحل 2 و 3
آخرین مرحله، تکرار مراحل 2 و 3 است. این تکرارها تا زمانی ادامه می یابد که معیار پایانی تحقق یابد. معیار پایانی ممکن است شامل موارد زیر باشد:
- رسیدن به مقدار مشخصی از دقت: اگر مقدار تابع در نقطه فعلی، کمتر از یک مقدار مشخص باشد، می توان گفت که روش گرادیان به کمینه محلی رسیده است.
- رسیدن به تعداد مشخصی از تکرار: اگر تعداد تکرارهای روش گرادیان به یک مقدار مشخص برسد، می توان گفت که روش گرادیان به نقطه ای رسیده است که دیگر نمی تواند بهبود یابد.
- رسیدن به نقطه ای که گرادیان آن صفر باشد: اگر گرادیان تابع در نقطه فعلی صفر باشد، می توان گفت که روش گرادیان به نقطه ای رسیده است که دیگر نمی تواند حرکت کند.
در پایان باید توجه داشته باشید که روش گرادیان ممکن است در مواردی که تابع دارای چندین کمینه یا بیشینه محلی باشد، کارآمد نباشد. در این موارد، ممکن است لازم باشد از روش های بهینه سازی دیگری استفاده شود.
الگوریتم های حل روش گرادیان
روش گرادیان را می توان با استفاده از انواع مختلف الگوریتم ها پیاده سازی کرد. برخی از الگوریتم های رایج عبارتند از:
- روش گرادیان ساده: روش گرادیان ساده ساده ترین الگوریتم است. در این الگوریتم، اندازه قدم برداشته شده در هر تکرار ثابت است.
- روش گرادیان کاهش وزن: روش گرادیان کاهش وزن یک الگوریتم بهبود یافته است. در این الگوریتم، اندازه قدم برداشته شده در هر تکرار به تدریج کاهش می یابد. این به جلوگیری از پرش از کمینه یا بیشینه محلی کمک می کند.
- روش گرادیان تصادفی: روش گرادیان تصادفی یک الگوریتم ابتکاری است. در این الگوریتم، در هر تکرار، علاوه بر حرکت در جهت مخالف گرادیان، یک حرکت تصادفی نیز انجام می شود. این به یافتن کمینه یا بیشینه محلی بهتر کمک می کند.
روش گرادیان ساده
روش گرادیان ساده ساده ترین الگوریتم است. در این الگوریتم، اندازه قدم برداشته شده در هر تکرار ثابت است.
الگوریتم حل گرادیان ساده
الگوریتم گرادیان در قالب روش فرانک- ولف مطرح شده است. در روش فرانک- ولف حرکت از یک نقطه شدنی ( Xi ) شروع می شود و از آن جا به منظور دسترسی به یک جهت بهینه حرکت (di) به نقطه جدید (yi) می رسد به طوری که خواهیم داشت: ( di = (yi – Xi سپس باید مقدار بهینه حرکت (λi) تعیین شود.
برای یافتن مقدار بهینه حرکت مسئله بهینه سازی زیر باید حل شود:
بهینه کنید: f (Xi + λi di )
s.to: λi ≥ 0
برای یافتن نقطه مقصد مدل زیر باید حل شود:
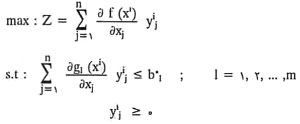
مدل گرادیان برای حل یک مسئله K هدفه
max: U {f1 (x), f2 (x), …. fk (x)} = U (F)
s.t: x ∈ S ; s = {x | gi(x) ≤ 0 ; i = 1, 2, …, m }
در این مدل توابع (f(x و (g(x به طور عینی معلوم است اما تابع مطلوبیت (U(F به طور ضمنی مد نظر است.
مفروضات استفاده از شرایط فرانک- ولف
- مجموعه متشکل از محدودیت ها محدب و بسته (مرزدار) باشد
- (U(F (تابع مطلوبیت توابع هدف) بر روی X مشتق پذیر و مقعر باشد
- هر یک از توابع هدف مقعر باشد
- مشتق جزئی تابع مطلوبیت نسبت به تابع هدف اول مثبت باشد که در نتیجه این تابع هدف به عنوان هدف مرجع تلقی می گردد
الگوریتم روش گرادیان یک مسئله K هدفه
قدم یکم: نقطه شروع xi ∈ S را انتخاب نموده و قرار دهید i=1
قدم دوم: راه حل بهینه yi را به منظور جهت یابی برای حرکت بهبودبخش از مسئله زیر بیابید:
max: ∇x U = (f1 (xi), f2 (xi), …. fk (xi)) . yi
s.t : yi ∈ S
بخش اساسی تعامل با خبره در همین جا است زیرا (U(F به طور عینی مشخص نیست و نیاز به کمک خبره دارد. فرض بر آن است که خبره قادر است تعدیل بین هر دو هدف از اهداف مسئله را به ازای یک راه حل مشخص برآورد کند. این نرخ حاشیه ای جایگزینی بین اهداف را می توان برای برآورد گرادیان از (U(F به کار برد. اثبات ریاضی این موضوع در ادامه ارائه شده است.
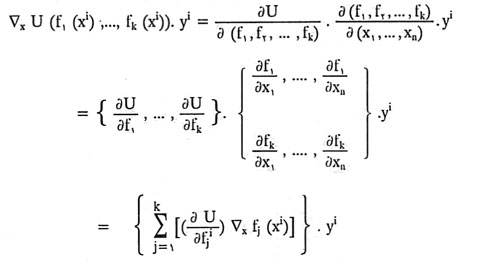
مدل بهینه سازی با تقسیم بر یک عدد ثابت تغییری نمی کند به این دلیل تابع هدف مذکور را بر (U∂/∂Fi1) تقسیم می کنیم.
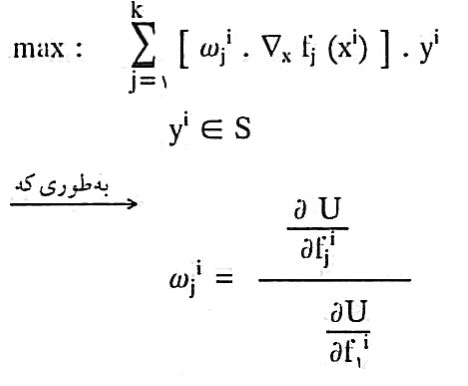
اوزان منعکس کننده تعدیل خبره بین اهداف است زیرا:
حال در ادامه جهت بدست آوردن اوزان wij باید نرخ حاشیه ای جایگزینی بین اهداف اول و jام را به کمک خبره ارزیابی نمود بدین صورت که تعدیل بی تفاوتی خبره از تغییر بسیار کوچک در هدف اول Δf1 در مقابل تغییر لازم برای هدف jام را جویا شویم. یعنی تغییر در هدف اول به میزان Δf1 با ثابت نگه داشتن بقیه اهداف به استثنای هدف jام چه اندازه از این هدف را جبران خواهد نمود. این برآورد به صورت زیر است:
wij = Δf1/Δfj
قدم سوم: مقدار بهینه λi را از مدل روبرو محاسبه نمائید:
max: U { F (Xi + λi di ) }
s.to: 0 ≤ λi ≤ 1
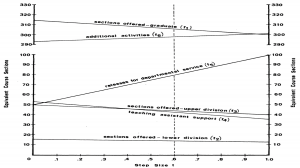
برای انجام این برآورد باید از نظرات خبره استفاده کرد. برای این کار به دو طریق می توان عمل نمود:
- رسم نمودار
- رسم جدول
روش گرادیان روش گرادیان روش گرادیان روش گرادیان روش گرادیان
قدم چهارم: اختتام الگوریتم
از نظر تئوری پایان الگوریتم زمانی است که دو راه حل متوالی با یکدیگر یکسان شوند ولی این ایده آل به ندرت اتفاق می افتد. به همین دلیل نسبتی را به نام نسبت بهبودی تعریف می کنیم که یک معیار عملی برای پایان الگوریتم است:
به منظور شفاف سازی حل روش گرادیان، در ادامه مثالی ذکر شده است.
مثال روش گرادیان
مساله روبرو ر با 3 تابع هدف و 4 محدودیت در نظر بگیرید. با استفاده از روش گرادیان نقاط بهینه تابع را بدست آورید.
Max f1(x)= – x1 – 2 x2 – 3 x3
f2(x) = – x1 – 2 x2 – x3
f3(x) = -2×1 – x2 –x3
S . to :
2×1 + 5×2 + 3 x3 ≥ 30
x1 + x2 + x3 ≥ 18
10×1 + 8×2 + 4 x3 ≥40
3×1+2×2 ≥20
x1 , x2 , x3 ≥ 0
انتقال یکم :
گام اول) تعیین نقطه عملی
x’ ∈ S -> x1= (2, 9, 7) , i=1 , ε =0.15
مفروضات مسئله:
F0 = {F1(x1), F2(x1), F3(x1)} -> F0 = { (-41, -27, -20)
گام دوم) راه حل بهینه
قدم دوم : (f1 در مقابل f2)
{(-41-20 ) , ( -27 + 2 ) , ( -20 )} = > w12=-(2/-20) = 0.1
قدم دوم : (f2 در مقابل f3)
{(-41) , ( -27 + 2 ) , ( -20- 10 )}= > w13=-(2/-10) = 0.2 -> w1=(0.1 , 1, 0.2)
محاسبه (Y1, d1 )= 0.1(-1 , -2 , -3 ) Y1 +1( -1 , -2 , -1) Y1 + 0.2 ( -2 , -1 , -1 ) Y1
Y1={Y11 , Y21 , Y31 }
Max: 0.1f1(Y1) + 1f2(Y1)+ 0.2 f3(Y1)
S.to Y1 ∈ S
S فضای حاصل از محدودیتهای مسئله:
Y1 = {0, 0, 10} d1= = {(0 – 2), (0 – 9), (10 – 7)} = {-2, – 9, 3}
گام سوم ) تعیین نمودن نقطه بهینه
برای f1 داریم ( محاسبات برای 0.2= λو 0.4= λو 0.6= λو 0.8= λ و اگر 1= λ) :
-1 ( 2 + .2 ( -2 )) -2 ( 9 + .2 ( -9 ))-3( 7 + .2 ( 3 )) =-38.8
-1 ( 2 + .4 ( -2 )) -2 ( 9 + .4 ( -9 ))-3( 7 + .4 ( 3 )) =- 36.7
-1 ( 2 + .6 ( -2 )) -2 ( 9 + .6 ( -9 ))-3( 7 + .6 ( 3 )) =-34.4
-1 ( 2 + .8 ( -2 )) -2 ( 9 + .8 ( -9 ))-3( 7 + .8 ( 3 )) =-32.1
-1 ( 2 + 1 ( -2 )) -2 ( 9 + 1 ( -9 ))-3( 7 + 1 ( 3 )) =-30
برای f2 داریم:
-1 ( 2 + .2 ( -2 )) -2 ( 9 + .2 ( -9 ))- ( 7 + .2 ( 3 )) =-23.6
-1 ( 2 + .4 ( -2 )) -2 ( 9 + .4 ( -9 ))- ( 7 + .4 ( 3 )) =- 20.2
-1 ( 2 + .6 ( -2 )) -2 ( 9 + .6 ( -9 ))- ( 7 + .6 ( 3 )) =-16.8
-1 ( 2 + .8 ( -2 )) -2 ( 9 + .8 ( -9 ))- ( 7 + .8 ( 3 )) =-13.4
-1 ( 2 + 1 ( -2 )) -2 ( 9 + 1 ( -9 ))- ( 7 + 1 ( 3 )) =-10
و برای f3 داریم :
-2 ( 2 + .2 ( -2 )) -1 ( 9 + .2 ( -9 ))- ( 7 + .2 ( 3 )) =-18
-2 ( 2 + .4 ( -2 )) -1 ( 9 + .4 ( -9 ))- ( 7 + .4 ( 3 )) =- 16
-2 ( 2 + .6 ( -2 )) -1 ( 9 + .6 ( -9 ))- ( 7 + .6 ( 3 )) =-13.8
-2 ( 2 + .8 ( -2 )) -1 ( 9 + .8 ( -9 ))- ( 7 + .8 ( 3 )) =-12
-2 ( 2 + 1 ( -2 )) -1 ( 9 + 1 ( -9 ))- ( 7 + 1 ( 3 )) =-10
| 1=λ1 | 0.8=λ1 | 0.6=λ1 | 0.4=λ1 | 0.2=λ1 | 0=λ1 | |
| -30 | -32.1 | -34.4 | -36.7 | -38.8 | -41 | F1 |
| -10 | -13.4 | -16.8 | -20.2 | -23.6 | -27 | F2 |
| -10 | -12 | -13.8 | -16 | -18 | -20 | F3 |
در صورتی که 0.4=λ مورد نظر خبره باشد: ( -36.7 , – 20.2 , -16 )
به منظور انتقال به مرحله دوم باید محاسبه شود :
x2= ( X1 + λ1 d1)
x2= 2+ 0.4 -2=1.2
x2= 9+ 0.4 -9=5.4
x2= 7+ 0.4 3=8.2
x2= ( 1.2 , 5.4 , 8.78 ) -> F ={ (-38.34) , ( -20.78 ) , ( -16.58 ) }
قدم چهارم: کلیه گام ها مانند قبل تکرار می شود و مقدار ( -47.636 , -19.032 , -17.422 ) = F2 بدست می آید. حال شرط خاتمه بررسی می شود که در صورت تصدیق میزان بهینگی الگوریتم از حرکت باز می ایستد.
از ε =0.15 کمتر است پس در همین تکرار متوقف می شود.
تصمیم گیری چند معیاره
تصمیمگیری شامل بیان درست اهداف، تعیین راهحلهای مختلف و ممکن، ارزیابی امکانپذیری آنان، ارزیابی عواقب و نتایج ناشی از اجرای هر یک از راهحلها و بالاخره انتخاب و اجرای آن میباشد. کیفیت مدیریت اساساً تابع کیفیت تصمیمگیری است زیرا کیفیت طرح و برنامهها، اثربخشی و کارآمدی راهبردها و کیفیت نتایجی که از اعمال آنها بدست میآید همگی تابع کیفیت تصمیماتی است که مدیر اتخاذ مینماید.
در اکثر موارد تصمیمگیریها وقتی مطلوب و مورد رضایت تصمیمگیرنده است که تصمیمگیری براساس چندین معیار مورد بررسی قرار گرفته باشد. معیارها ممکن است کمی یا کیفی باشند. در روشهای تصمیمگیری چند معیاره که در دهههای اخیر مورد توجه محققین قرار گرفتهاست به جای استفاده از یک معیار سنجش بهینگی از چند معیار سنجش استفاده میشود.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.
روش گرادیان چگونه کار می کند؟
روش گرادیان بر اساس این اصل است که هر نقطه در فضای جستجو دارای یک گرادیان است که جهت افزایش سریعترین تابع را نشان می دهد. با حرکت به سمت مخالف گرادیان، به سمت کمینه یا بیشینه محلی حرکت می کنیم.
چه زمانی از روش گرادیان استفاده می شود؟
روش گرادیان یک روش ساده و موثر است که برای طیف گسترده ای از مسائل بهینه سازی استفاده می شود. از جمله موارد زیر:
*یافتن کمینه یا بیشینه محلی یک تابع
*حل مسائل بهینه سازی خطی
*حل مسائل بهینه سازی غیرخطی
چه زمانی از روش گرادیان استفاده نمی شود؟
روش گرادیان ممکن است در مواردی که تابع دارای چندین کمینه یا بیشینه محلی باشد، کارآمد نباشد. در این موارد، ممکن است لازم باشد از روش های بهینه سازی دیگری استفاده شود.
مزایای روش گرادیان چیست؟
مزایای روش گرادیان عبارتند از:
*سادگی
*کارایی
*قابلیت استفاده برای طیف گسترده ای از مسائل
معایب روش گرادیان چیست؟
معایب روش گرادیان عبارتند از:
*ممکن است در مواردی که تابع دارای چندین کمینه یا بیشینه محلی باشد، کارآمد نباشد.
*ممکن است به نقطه ای که گرادیان آن صفر باشد، برسد که این نقطه لزوما کمینه یا بیشینه محلی نیست.
چگونه می توان کارایی روش گرادیان را بهبود بخشید؟
برای بهبود کارایی روش گرادیان، می توان از روش های مختلفی استفاده کرد. به عنوان مثال، می توان از روش های زیر استفاده کرد:
*استفاده از روش گرادیان کاهش وزن
*استفاده از روش گرادیان تصادفی
*استفاده از روش های بهینه سازی ترکیبی