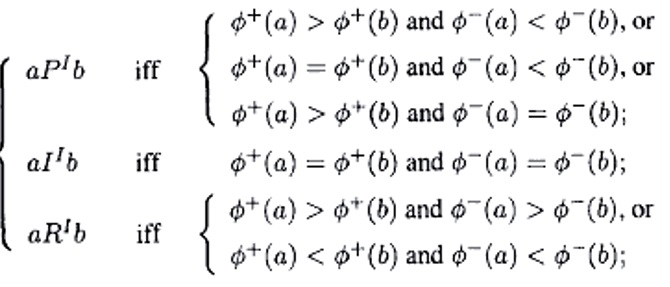روش promethee

روش promethee روش ساختار یافته ی رتبه بندی ترجیحی برای غنی سازی ارزیابی ها جزء روشهای MADM و به عنوان یك روش كارا و با استفاده از دو واژه ترجیح و بی تفاوتی به دنبال انتخاب بهترین گزینه می باشد.

روش promethee

روش promethee

این روش در زمینه های مختلف همانند بانکداری، مناطق صنعتی، برنامه ریزی نیروی کاری، منابع آب، سرمایه گذاری ها، پزشکی، شیمی ،مراقبت های پزشکی، تحقیق در عملیات، مدیریت پویا و . . . به كار گرفته شده است. این روش به دلیل خاصیت ریاضی و سهولت استفاده از آن جزء روشهای پر استقبال قرار گرفته است.

این روش توسط دو استاد بلژیکی به نام ژان پیر برنز و برتراند مارسکال در دهه 1980 ارائه شد. در واقع پس این شروع پرومته توسعه یافت و از آن در شرایط مختلف نسخه هایی به وجود آمد. و می توان از آنها با عنوان خانواده پرومته یاد كرد.

مزایای روش promethee

• قابلیت انعطاف‌پذیری: روش پرومته برای حل مسائل مختلف با معیارهای متنوع و گاه متضاد، قابل استفاده است.
• توانایی در نظر گرفتن ترجیحات تصمیم‌گیرنده: این روش با در نظر گرفتن ترجیحات و نظرات شما در فرآیند تصمیم‌گیری، انتخابی ایده‌آل و متناسب با نیازهایتان را به ارمغان می‌آورد.
• ارائه اطلاعات دقیق: روش پرومته با ارائه اطلاعات دقیق در مورد برتری و ترجیح گزینه‌ها، به شما در انتخابی مطمئن و با آگاهی کامل کمک می‌کند.

کاربردهای روش promethee

روش پرومته به عنوان یک روش قدرتمند در تصمیم‌گیری چندمعیاره، در زمینه‌های مختلفی کاربرد دارد. برخی از کاربردهای این روش عبارتند از:

انتخاب:

• بهترین تامین‌کننده: با توجه به معیارهایی مانند قیمت، کیفیت، زمان تحویل و …
• بهترین پروژه: با توجه به معیارهایی مانند سودآوری، ریسک، زمان انجام و …
• بهترین محل: برای احداث یک کارخانه، با توجه به معیارهایی مانند دسترسی به مواد اولیه، نیروی کار، بازار و …
• بهترین شغل: با توجه به معیارهایی مانند حقوق، مزایا، فرصت‌های پیشرفت، علاقه و …
• بهترین رشته تحصیلی: با توجه به معیارهایی مانند علاقه، بازار کار، رتبه دانشگاه و …

رتبه‌بندی:

• دانشگاه‌ها: با توجه به معیارهایی مانند کیفیت آموزشی، امکانات رفاهی، رتبه علمی و …
• بیمارستان‌ها: با توجه به معیارهایی مانند کیفیت خدمات، تخصص پزشکان، هزینه و …
• محصولات: با توجه به معیارهایی مانند قیمت، کیفیت، کارایی، برند و …
• پروژه‌های تحقیقاتی: با توجه به معیارهایی مانند نوآوری، اهمیت، امکان‌پذیری و …

انتخاب و رتبه‌بندی در:

• بانکداری: انتخاب بهترین طرح تسهیلات
• بیمه: انتخاب بهترین نوع بیمه
• بازاریابی: انتخاب بهترین استراتژی بازاریابی
• تولید: انتخاب بهترین روش تولید
• منابع انسانی: انتخاب بهترین روش استخدام

انواع روش های promethee : تنوعی برای انتخابی دقیق

روش پرومته در دو نوع اصلی ارائه شده است که هر کدام مزایا و معایب خاص خود را دارند:

1. روش promethee 1:

• مبتنی بر ماتریس ترجیحات: این روش از ماتریس ترجیحات برای رتبه‌بندی گزینه‌ها استفاده می‌کند.
• سادگی و سهولت استفاده: روش promethee 1 به دلیل سادگی و سهولت استفاده، برای حل مسائل ساده‌تر مناسب است.
• محاسبات کم: این روش به محاسبات کمتری نسبت به روش پرومته 2 نیاز دارد.

2. روش پرومته 2:

• مبتنی بر ماتریس جریان ورودی و خروجی: این روش از ماتریس جریان ورودی و خروجی برای رتبه‌بندی گزینه‌ها استفاده می‌کند.
• اطلاعات دقیق‌تر: روش promethee 2 اطلاعات دقیق‌تری در مورد برتری و ترجیح گزینه‌ها ارائه می‌دهد.
• قابلیت در نظر گرفتن ترجیحات غیرخطی: این روش قادر به در نظر گرفتن ترجیحات غیرخطی تصمیم‌گیرنده است.
• محاسبات پیچیده‌تر: روش promethee 2 به محاسبات پیچیده‌تری نسبت به روش پرومته 1 نیاز دارد.

• promethee III ، روابط ترجیح و غیر ترجیح را بر اساس میانگین و انحراف معیار شاخص های ترجیح تعریف می كند.
• promethee IV، برای گزینه های نا محدود كاربرد دارد.
• promethee V، یك روش چند معیاره برای انتخاب گزینه ها همراه با لحاظ كردن محدودیت ها تعریف می كند.
• promethee VI، الگویی از مغز انسان است.

انتخاب روش مناسب:

انتخاب روش مناسب از بین دو روش promethee 1 و 2 promethee به عوامل مختلفی مانند ماهیت مسأله، ترجیحات تصمیم‌گیرنده و در دسترس بودن اطلاعات بستگی دارد. علاوه بر دو روش اصلی، روش‌های دیگری نیز از خانواده پرومته وجود دارند که عبارتند از:

• promethee 3: برای تحلیل روابط ترجیح و غیرترجیح
• promethee 4: برای حل مسائل با تعداد گزینه‌های نامحدود
• promethee 5: برای حل مسائل با محدودیت
• promethee 6: برای شبیه‌سازی مغز انسان در تصمیم‌گیری

مزایای روش promethee :

• سادگی و شفافیت: روش پرومته به زبان ساده قابل فهم و اجرا است.
• قابلیت انعطاف‌پذیری: این روش برای حل مسائل مختلف با معیارهای متنوع قابل استفاده است.
• توانایی در نظر گرفتن ترجیحات تصمیم‌گیرنده: روش پرومته امکان اعمال ترجیحات تصمیم‌گیرنده در فرآیند تصمیم‌گیری را فراهم می‌کند.
• ارائه اطلاعات دقیق: روش پرومته اطلاعات دقیقی در مورد برتری و ترجیح گزینه‌ها ارائه می‌دهد.

معایب روش promethee :

• محاسبات پیچیده: در برخی از موارد، محاسبات مربوط به روش پرومته می‌تواند پیچیده باشد.
• نیاز به اطلاعات: برای استفاده از روش پرومته به اطلاعات کامل و دقیقی در مورد معیارها و گزینه‌ها نیاز است.

الگوریتم روش promethee

در این روش باید دانست كه:

• این روش در زمره روشهای جبرانی قرار می گیرد
• شاخصهای كیفی به كمی تبدیل می شوند.
• نیازی نیست كه شاخص ها حتما مستقل از هم باشند.
• تصمیم گیرنده با n گزینه متناهی مواجه است.

A={Ai І i=1,2,…,n}

• تصمیم گیرنده شاخص هایی را جهت تصمیم گیری معرفی می نماید.

‍C={Cj І j=1,2,…,k}

• در نظر گرفتن وزن (W) برای شاخص ها به طوری كه:

Σ wj =1

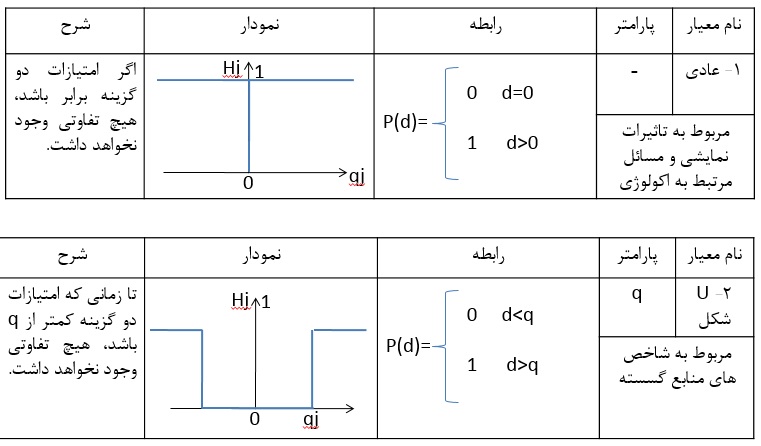
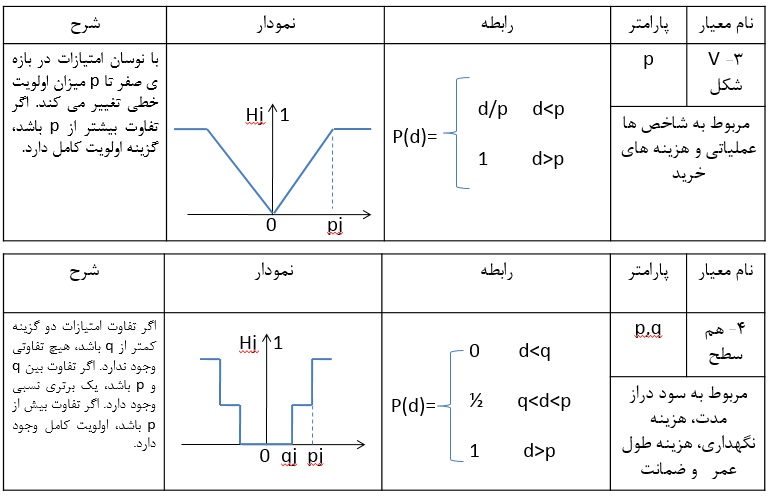
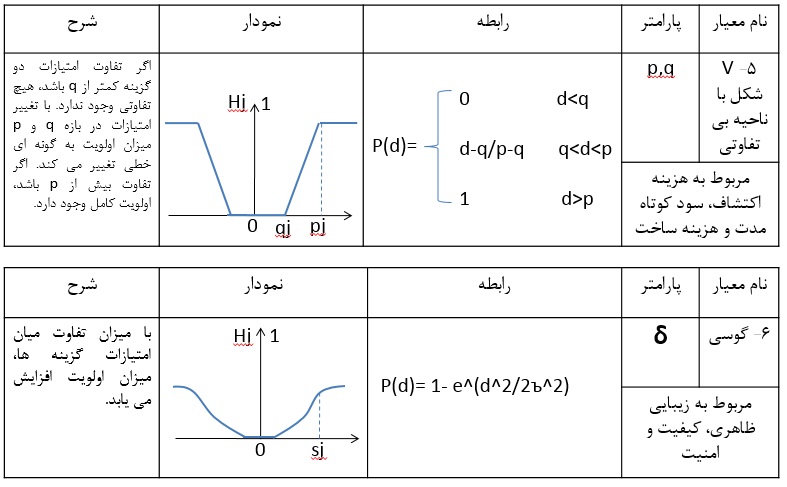
رتبه بندی گزینه ها با مقایسه زوجی گزینه ها در هر شاخص انجام می شود. مقایسه بر پایه یك تابع برتری از پیش تعریف شده با دامنه  [0,1] اندازه گیری می شود. تابع برتری (ترجیح) P، برای مقایسه ی دو گزینه ی a و b از نظر شاخص j به صورت زیر است:

Pj (a , b) = P[dj (a , b)]

گام اول تفاوت اندازه ها

(dj (a , b) = fj (a) – fj (b بیانگر تفاوت اندازه ها در شاخص j است. این تفاوت برای شاخص های Max زمانی معنادار خواهد بود كه (fj (a) > fj (b باشد. و برای شاخص Min این رابطه برعكس است.

گام دوم توابع برتری

پس از محاسبه میزان تفاوت گزینه ها با یكدیگر، مقدار (Pj(a,b و با توجه به توابع یاد شده بدست خواهد آمد.

روش promethee

گام سوم محاسبه موزون برتری

مجموع موزون برتری گزینه a نسبت به b كه آن را با (π(a,b نشان می دهند.

π(a,b) = Σ P_j(a,b)W_j

π(b,a) = Σ P_j(b,a)W_j

گام چهارم محاسبه جریان ورودی و خروجی

جریان ورودی و جریان خروجی در این گام صورت می پذیرد:

جریان خروجی: بیان می کند یک گزینه مانند a چه قدر از گزینه های دیگر برتر است. هرچه این مقدار بیشتر باشد این گزینه برتر خواهد بود.

Φ⁺(a) = Σ π(a,x)

جریان ورودی: بیان می کند که گزینه های دیگر چه قدر برگزینه a برتر می باشند. هرچه این مقدار کمتر باشد این گزینه بهتر خواهد بود.

Φ^–(a) = Σ π(x,a)

گام پنجم رتبه‌بندی نهایی

رتبه بندی ها از مقایسه جریان های برتری مثبت و منفی به دست می آیند. که p و I و R به ترتیب نشان دهنده ارجحیت،بی تفاوتی و غیر قابل مقایسه بودن است.

• رابطه a p^I b نشان می دهد برتری a ناشی از ضعف b است.
• وقتی که a I^I b ، جریان های مثبت و منفی با هم برابرند.
• وقتی a R^I b قدرت بیشتر یک گزینه ناشی ازضعف گزینه دیگر است.در چنین حالتی اطلاعاتی که توسط دو جریان به وجود می آیند سازگار نیستند.

سوالات متداول

خدمات فرابگیر

1. تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
2. مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
3. برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
4. طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
5. خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
6. پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
7. آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت

باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.