فازی زدایی یا دیفازی سازی

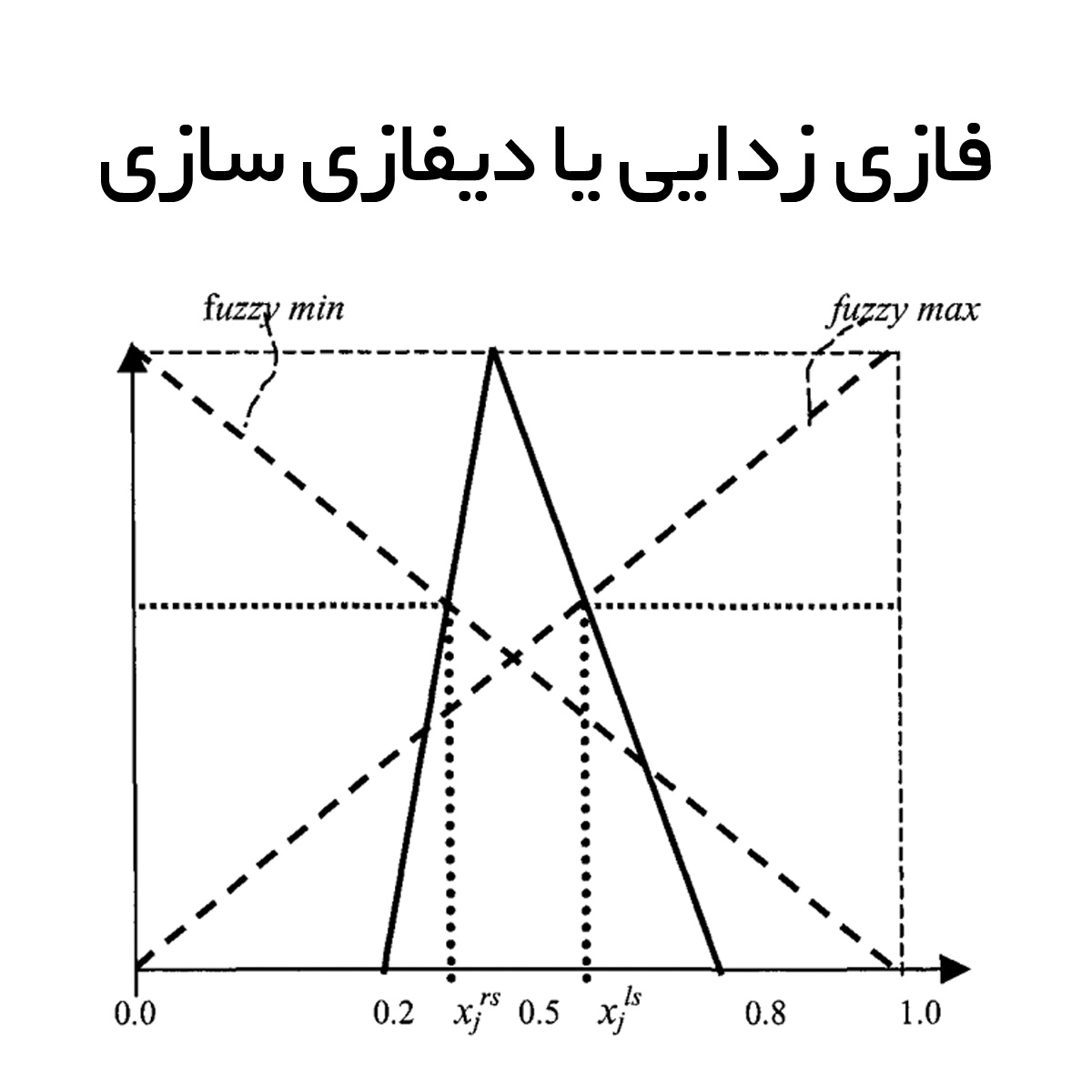
“فازی زدایی” انتخاب یک عنصر قطعی بر اساس خروجی مجموعه فازی است و شامل تبدیل اعداد فازی به اعداد قطعی می باشد.. روش متداول فازی زدایی، روش مرکز سطح (Centroid)، همراه با چندین روش دیگر، توسط یاگر و فایلو ارائه شده است. با این حال، عملیات فازی زدایـی را نمی توان به طور منحصر به فرد تعریف کرد.

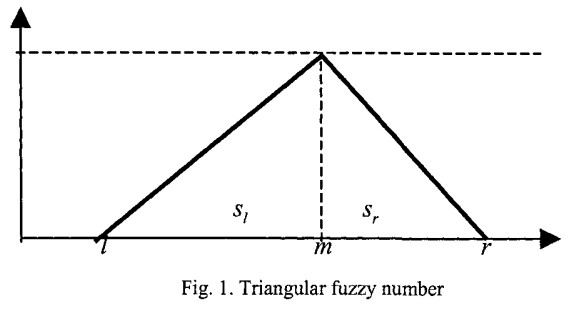
برای بیان یک مقدار غیر دقیق، به عنوان “حدود m” (“تقریبا m”)، از عدد فازی (N) استفاده می شود که با یک تابع عضویت مرتبط است (شکل 1). تابع عضویت x(N)µ نشان دهنده درجه صحت مقدار فازی برابر با x  در بازه واقعی [r,l] می باشد.

تصمیم گیری چندمعیاره (MCDM)  در یک محیط فازی نیاز به مقایسه اعداد فازی (مجموعه ها) دارد. مشکل مقایسه اعداد فازی مورد مطالعه قرار گرفته است و به نظر می رسد یک مشکل مهم و دشوار باشد. یک عدد فازی با شکل، گسترش، ارتفاع و موقعیت نسبی آن در محور x مشخص می شود. یک روش رتبه بندی خوب روشی است که همه این عوامل را در نظر بگیرد. چندین روش دیفازی سازی وجود دارد. از روش های رتبه بندی فازی که تاکنون توسعه یافته اند می توان برای مقایسه اعداد فازی استفاده کرد، اما هیچ یک از این روش های موجود کامل نیستند.

1) روش مرکز سطح (Centroid)

متداول‌ترین روش دیفازی سازی (فازی زدایی) مورد استفاده، روش Centroid (Centroid-of-Gravity) است که یک مقدار قطعی را بر اساس مرکز ثقل مجموعه فازی ارائه می‌کند. این یک روش میانگین وزنی است که در آن از تابع عضویت برای وزن دهی استفاده می شود. بر اساس این روش رابطه زیر برای تبدیل یک عدد فازی به عدد قطعی Xcrisp فرموله شده است.

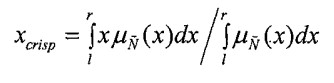
برای عدد فازی مثلثی N= (l,m,r) روابط معادل زیر را می توان مشتق کرد.

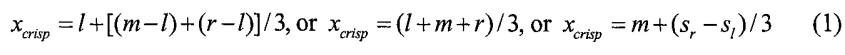
جایی که Sl و Sr به ترتیب در سمت چپ و راست “گسترش” هستند.

تابع مثلثی عضویت برای یک عدد فازی مثلثی به صورت زیر تعریف می شود:

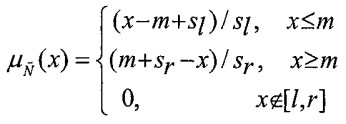
سپس با استفاده از رابطه (1) رابطه زیر به دست می آید:

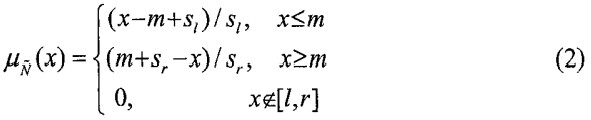
با توجه به معادلات (1) و (2) می توان نتیجه گرفت که:

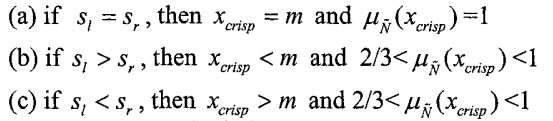
روش مرکز سطح یک مقدار واضح با حداکثر تابع عضویت 1= µ برای یک عدد فازی مثلثی متقارن می‌دهد (l-m=r-m) اما بین دو عدد فازی  با دو معنی m یکسان تمایز قائل نمی‌شود. یک نقطه ضعف روش غیرفازی مرکز سطح این است که دو عدد فازی با اشکال مختلف ممکن است مقدار قطعی  یکسانی داشته باشند.

2) روش چن و هوانگ

چن و هوانگ روشی را برای حل یک مسئله تصمیم گیری چندمعیاره فازی در دو مرحله پیشنهاد کردند. در مرحله اول تبدیل داده های تصمیم فازی به اعداد قطعی (فازی زدایی) و در مرحله دوم می توان یک روش تصمیم گیری کلاسیک را اعمال کرد. در اینجا تنها مرحله اول در نظر گرفته شده است. عدد قطعی Crisp (N) عدد فازی N به صورت زیر به دست می آید.

عدد سمت راست با استفاده از موارد زیر تعیین می شود:

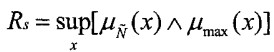
و عدد سمت چپ با استفاده از:

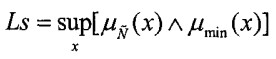
که در آن یک مجموعه حداکثر و یک مجموعه حداقل عبارتند از:

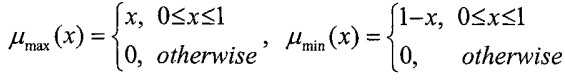
مجموع امتیاز قطعی Crisp(N) با استفاده از موارد زیر تعیین می شود:

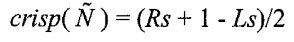
3) روش CFCS

روش فازی‌زدایی CFCS برای تبدیل اعداد فازی به امتیازهای قطعی به روشی مشابه روش چن و هوانگ توسعه داده شده است. امتیازهای فازی مربوطه به اعداد قطعی با استفاده از روشی مشابه با رویکرد تعیین امتیاز چپ و راست به ترتیب حداقل و حداکثر فازی تعیین می‌شوند و نمره کل با توجه به توابع عضویت به صورت میانگین موزون تعیین می شود.

فرض کنید که گزینه ها بر اساس معیار iام اعداد فازی Fij، به طوری که J تعداد گزینه ها است، تعیین می شوند. برای اعداد فازی مثلثی Fij =(lij,mij,uij)، مقدار قطعی معیار j’-ام را می توان با الگوریتم چهار مرحله ای CFCS به صورت زیر تعیین کرد:

1) نرمال سازی (عادی سازی):

برای همه گزینه ها aj , j=1,…,J محاسبه کنید:

2) مقادیر نرمال شده چپ (Is) و راست (rs) را برای   j=1,…,J محاسبه کنید.

3) مجموع مقدار قطعی نرمال شده را برای   j=1,…,J  محاسبه کنید.

4) مقدار امتیاز قطعی را را برای   j=1,…,J  محاسبه کنید.

این روش چهار مرحله‌ای CFCS برای همه معیارهای fi، fi€n انجام می‌شود، یعنی n مجموعه‌ای از معیارهای ارزیابی شده با اعداد فازی را نشان می‌دهد. تمام مقادیر Fij =(lij,mij,uij)  از i امین معیار در محاسبات گنجانده شده است، حتی اگر همه گزینه ها با اعداد فازی ارزیابی نشوند. برخی از این مقادیر می تواند قطعی باشند.(l=m=u)

ویژگی های اصلی روش فازی زدایی CFCS

• می تواند برای یک مدل تصمیم گیری چندمعیاره با مجموعه ای ترکیبی از معیارهای قطعی و فازی استفاده شود
• برای تبدیل اعداد فازی به اعداد قطعی قابل استفاده است.
• تبدیل با در نظر گرفتن تابع عضویت و موقعیت نسبی در محور x.
• از تابع عضویت به عنوان یک تابع وزن در تبدیل استفاده می کند.

با استفاده از روش CFCS ، برای هر معیار، اعداد فازی که مقادیر معیار را برای همه گزینه‌ها نشان می‌دهند، به طور جداگانه به اعداد قطعی تبدیل می‌شوند. به این ترتیب، یک ماتریس عملکرد با عناصر فازی به یک ماتریس با اعداد قطعی تبدیل می شود که می تواند در یک روش تصمیم گیری چند معیاره مانند TOPSIS یا VIKOR یا روش های دیگر مورد استفاده قرار گیرد.

در ادامه می توانید مثال های انواع روش های فازی زدایی بالا را مشاهده نمایید.