مثال روش جستجوی طلایی
با استفاده از روش جستجوی طلایی نقطه x را طوری تعیین نمایید که تابع هدف f(x) = x4-14x3+60x2-70x را در بازه [0, 2] کمینه می نمایید. طول بازه را 0.3 در نظر بگیرید.
مثال روش جستجوی طلایی
به منظور یافتن تعداد تکرار جهت کمینه شدن از فرمول فوق استفاده می نماییم:
(0.3/2) = (0.61803)N -> N =4 تعداد تکرار
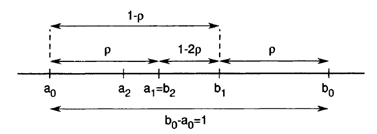
تکرار اول: تابع f را در دو نقطه میانی a1 و b1 در نظر می گیریم. خواهیم داشت:
a1 = a0 + p (b0 –a0) = 0.7639
b1 = a0 + p (1 – p) (b0 –a0) = 1.236
مقدار p = (3-√5)/2 پس
f (a1) = -24.36 f(b1) = -18.96
از آنجایی که مقدار f(a1) < f(b1) است، لذا بازه عدم قطعیت کاهش یافته و برابر [a0 ,b1] = [0, 1.236] خواهد بود.
تکرار دوم: نقطه b2 را به عنوان نقطه منطبق با a1 در نظر می گیریم لذا تنها به ارزیابی در یک نقطه جدید نیاز خواهیم داشت:
a2 = a0 + p (b1 –a0) = 0.4721
f (a2) = -21.10 f(b2) = f(a1) = -24.36
از آنجایی که مقدار f(b2) < f(a2) است، لذا بازه عدم قطعیت کاهش یافته و برابر [a2 ,b1] = [0.4721, 1.236] خواهد بود.
تکرار سوم: نقطه a3 را به عنوان نقطه منطبق با b2 در نظر می گیریم لذا تنها به ارزیابی در یک نقطه جدید نیاز خواهیم داشت:
b3 = a2 +(1- p) (b1 –a2) = 0.9443
f (a3) =f (b2) = -24.36 f(b2) = f(a1) = -23.59
از آنجایی که مقدار f(b3) > f(a3) است، لذا بازه عدم قطعیت کاهش یافته و برابر [a2 ,b3] = [0.4721, 0.9443] خواهد بود.
تکرار چهارم: نقطه .b4 = a3
a4 = a2 + p (b3 –a2) = 0.6525
f (a4) = -23.84 f(b4) = f(a3) = -24.36
از آنجایی که مقدار f(a4) > f(b4) است، لذا بازه عدم قطعیت کاهش یافته و برابر [a2 ,b3] = [0.6525, 0.9443] خواهد بود.
حال تفریق b3 – a4 = 0.292 خواهد بود که از مقدار 3 کمتر است و ما به نقطه مورد نظر دست پیدا نمودیم.