قبل از تشریح مثال روش جستجوی فیبوناچی بهتر است با کلیات این روش آشنا شویم. در سال 1962، دو ریاضیدان به نامهای Kiefer و Wolfowitz روش جستجوی فیبوناچی را برای یافتن ریشه معادلات غیرخطی ارائه دادند.
آنچه می خوانید
این روش از دنباله فیبوناچی برای تقسیم بازه جستجو به دو قسمت با نسبتهای خاص استفاده میکند. این تقسیمبندی به الگوریتم اجازه میدهد تا به طور کارآمد به ریشه معادله نزدیک شود.
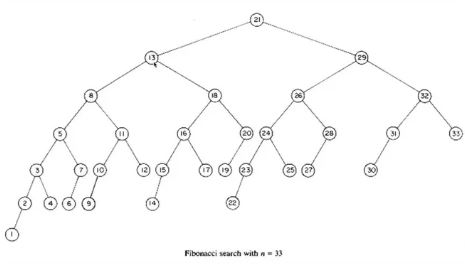
مثال روش جستجوی فیبوناچی
فرض کنید می خواهیم ریشه معادله زیر را با استفاده از روش جستجوی فیبوناچی پیدا کنیم.
F(x) = x4 – 14x3 + 60x2 -70x
از روش جستجوی فیبوناچی به منظور یافتن مقدار x که مقدارf بر روی بازه [0, 2] استفاده نمایید. مقدار x را در میان بازه 0.3 قرار دهید. بعد از N تکرار در بدترین وضعیت بازه جواب توسط (1+2e)/FN+1 کاهش خواهد یافت. لذا باید مقدار N را به صورت زیر انتخاب نماییم.
(1+2e)/FN+1 ≤ بازه نهایی / بازه اولیه ≤ 0.3 /2 = 0.15
لذا باید
FN+1 ≥ (1 + 2e) / 0.15
اگر مقدار e ≤ 0.1 باشد، سپس N =4 خواهد بود.
تکرار اول مثال روش جستجوی فیبوناچی
با این مقدار شروع می کنیم:
1 – P1 = F4 / F5 = 5/8.
حال مقادیر زیر را محاسبه می نماییم:
a1 = a0 + P1 (b0 – a0) = 3/4. b1 = a0 + (1-P1) (b0 – a0) = 5/4.
f(a1) = -24.34 f(b1) = -18.65 f(a1) < f(b1).
بازه به صورت زیر کاهش می یابد:
[a0, b1] = [0, 5/4]
تکرار دوم مثال روش جستجوی فیبوناچی
با این مقدار شروع می کنیم:
1 – P2 = F3 / F4 = 3/5.
حال مقادیر زیر را محاسبه می نماییم:
a2 = a0 + P2 (b1 – a0) = 1/2. b2 = a1 = 3/4
f(a2) = -21.69 f(b2) =f(a1) = -24.34 f(a2) > f(b2).
بازه به صورت زیر کاهش می یابد:
[a2, b1] = [1/2, 5/4]
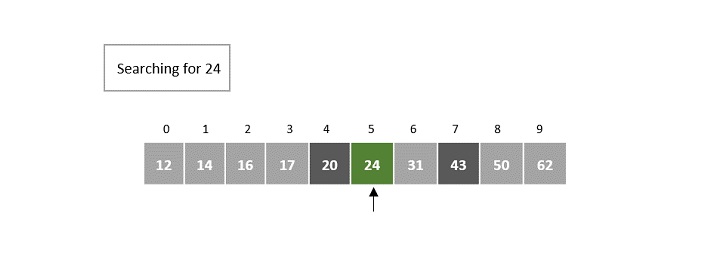
تکرار سوم مثال روش جستجوی فیبوناچی
با این مقدار شروع می کنیم:
1 – P3 = F2 / F3 = 2/3.
حال مقادیر زیر را محاسبه می نماییم:
a3 = b2= 3/4. b3 = a2 + (1 – p3) (b1 – a2) = 1
f(a3) = f(b2) = -24.34 f(b3) = -23 f(a3) < f(b3).
بازه به صورت زیر کاهش می یابد:
[a2, b3] = [1/2, 1]
تکرار چهارم مثال روش جستجوی فیبوناچی
با این e = 0.05 شروع می کنیم:
1 – P4 = F1 / F2 = 1/2.
حال مقادیر زیر را محاسبه می نماییم:
a4 = a2 + (p4 – e) (b3 – a2) = 0.725. b4 = a3 = 3/4.
f(a4) = -24.27 f(b4) = f(a3) = -24.34 f(a4) > f(b4).
بازه به صورت زیر کاهش می یابد:
[a2, b3] = [0.725, 1] (b3 – a2) => 1 – 0.725 = 0.275 <0.3.
از مقدار تعیین شده کمتر می باشد لذا متوقف می شویم.
سوالات متداول
روش جستجوی فیبوناچی چیست؟
روش جستجوی فیبوناچی (Fibonacci Search Method) یک الگوریتم عددی برای یافتن ریشه معادلات غیرخطی تک متغیره است. این روش از دنباله اعداد فیبوناچی برای تقسیم و جستجوی هوشمندانه بازه جستجو استفاده میکند.
مزایای روش جستجوی فیبوناچی چیست؟
عدم نیاز به مشتق: برخلاف روش نیوتن-رافسون، روش جستجوی فیبوناچی نیازی به محاسبه مشتق تابع ندارد.
پایداری: روش جستجوی فیبوناچی در مقایسه با روش نیوتن-رافسون از نظر عددی پایدارتر است.
کاربرد گسترده: روش جستجوی فیبوناچی را می توان برای حل طیف وسیعی از معادلات غیرخطی تک متغیره به کار برد.
معایب روش جستجوی فیبوناچی چیست؟
سرعت همگرایی: به طور کلی، سرعت همگرایی روش جستجوی فیبوناچی کندتر از روش نیوتن-رافسون است. محاسبات: این روش نیاز به محاسبه دنباله فیبوناچی دارد که می تواند زمان بر باشد. عدم وجود ضمانت همگرایی: برخلاف روش نیوتن-رافسون، روش جستجوی فیبوناچی ضمانتی برای همگرایی به ریشه معادله ارائه نمی دهد.
کاربردهای روش جستجوی فیبوناچی چیست؟
مهندسی: تحلیل سازه ها، طراحی سیستم ها، کنترل فرآیندها
علوم کامپیوتر: هوش مصنوعی، یادگیری ماشین، پردازش تصویر
مسائل مالی: تحلیل سهام، مدیریت ریسک، قیمت گذاری اوراق قرضه
علوم پایه: فیزیک، شیمی، زیست شناسی، ریاضیات
پزشکی: تصویربرداری پزشکی، تشخیص بیماری، درمان بیماری
چگونه می توانم روش جستجوی فیبوناچی را پیاده سازی کنم؟
پیاده سازی روش جستجوی فیبوناچی در زبان های برنامه نویسی مختلف مانند پایتون، جاوا، C++ و MATLAB امکان پذیر است. کدهای مختلفی برای پیاده سازی این روش در اینترنت موجود است. ما در فرابگیر این کد را برای شما اماده کرده ایم.
چه روش های دیگری برای یافتن ریشه معادلات غیرخطی وجود دارد؟
روش نیوتن-رافسون
روش تنظیم خطی
روش برنت
روش دنباله نصف کردن
کدام روش برای یافتن ریشه معادلات غیرخطی بهتر است؟
انتخاب روش مناسب برای یافتن ریشه معادلات غیرخطی به عوامل مختلفی مانند نوع معادله، دقت مورد نظر، منابع محاسباتی موجود و تجربه کاربر بستگی دارد.
آیا می توان از روش جستجوی فیبوناچی برای حل معادلات دیفرانسیل استفاده کرد؟
خیر، روش جستجوی فیبوناچی برای حل معادلات تک متغیره
آیا می توان از روش جستجوی فیبوناچی برای حل مسائل بهینه سازی استفاده کرد؟
بله، روش جستجوی فیبوناچی را می توان برای حل این مسائل استفاده کرد.
از مشاوره با ما پشیمان نمی شوید
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.
