مثال روش ساو

مثال روش ساو

روش وزن‌دهی ساده یکی از نخستین و ساده‌ترین روش‌های تصمیم‌گیری چندشاخصه است. در این روش از یک ماتریس تصمیم برای ارزیابی تعدادی گزینه براساس تعدادی معیار استفاده می‌شود. اگرچه روش حل مساله با میانگین موزون تفاوت چندانی ندارد اما گام‌های انجام این روش مقدمه خوبی برای فراگیری سایر روش‌های تصمیم‌گیری چندشاخصه است.

روش SAW که مخفف Simple Additive Weighting است، امتیاز کلی یک راه حل کاندید با مجموع وزنی تمام مقادیر ویژگی تعیین می شود. روش ساده وزنی به دلیل سهولتی که دارد محبوب ترین و رایج ترین روش در MADM است.

روش SAW را می توان ساده ترین و مستقیم ترین روش مواجهه با مسائل تصمیم گیری چند معیاره در نظر گرفت. در این روش از یک تابع افزایش خطی برای نمایش ترجیحات تصمیم گیرندگان استفاده می شود . با این حال این تکنیک زمانی کاربرد دارد که فرض شود ترجیحات مستقل یا مجزا از هم هستند.

در این روش جهت تصمیم گیری، تنها به ماتریس تصمیم گیری و بردار وزن شاخص های ارزیابی نیاز است. این روش مانند روش ویکور و تاپسیس عمل می کند اما به روشی بسیار ساده تر. در این روش که با نام روش ترکیب خطی وزن دار نیز شناخته می شود، پس از بی مقیاس کردن ماتریس تصمیم، با استفاده از ضرایب وزنی معیارها، ماتریس تصمیم بی مقیاس وزن دار به دست آمده و با توجه به این ماتریس، امتیاز هر گزینه محاسبه می شود.

مثال: فرض کنید فردی می خواهد از بین سه نوع سیستم کامپیوتری ، با روش SAW یک نوع را انتخاب کند. هر نوع سیستم ، با پنج شاخص که عبارتند از هزینه، عمر مفید، کیفیت، خدمات پس از فروش، کیفیت سخت افزار و کیفیت نرم افزار ارزیابی می شود. ماتریس تصمیم گیری این مساله ، به صورت جدول زیر می باشد. گزینه ها با Ai  و  شاخص ها با Cj نشان داده شده اند.

معیار / گزینه	C1	C2	C3	C4	C5
A1	30	20	متوسط	خیلی زیاد	کم
A2	10	30	زیاد	متوسط	زیاد
A3	20	50	خیلی زیاد	کم	خیلی زیاد

گام اول: تبدیل شاخص کیفی به شاخص کمی. برای این کار می توان از مقیاس فاصله ی دو قطبی ( ساعتی) استفاده کرد.

معیار / گزینه	C1	C2	C3	C4	C5
A1	30	20	متوسط	خیلی زیاد	کم
A2	10	30	زیاد	متوسط	زیاد
A3	20	50	خیلی زیاد	کم	خیلی زیاد

از جدول متغیرهای کلامی معادل عددی آن را برای استفاده در ماتریس تصمیم نهایی استخراج می کنیم.

اصطلاح زبانی فارسی	اصطلاح زبانی لاتین	عدد متناظر
ترجیح کامل	Extremely preferred	9
ترجیح خیلی قوی	Very strongly preferred	7
ترجیح قوی	Strongly preferred	5
ترجیح کم	Moderately preferred	3
ترجیح یکسان	Equality preferred	1
ترجیحات بین فواصل		2,4,6,8

سپس معادل عددی کلیه معیارها را برای تشکیل ماتریس نهایی جایگزین می نماییم.

معیار / گزینه	C1	C2	C3	C4	C5
A1	30	20	5	9	3
A2	10	30	7	5	7
A3	20	50	9	3	9

مثال روش ساو مثال روش ساو مثال روش ساو

گام دوم: اکنون باید این ماتریس تصمیم کمی، بی مقیاس شود. نوع بی مقیاس سازی این روش تصمیم گیری چندشاخصه «بی مقیاس سازی خطی » می باشد ( توجه : شاخص اول منفی است. )

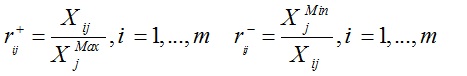
معیار / گزینه	C1-	C2+	C3+	C4+	C5+
A1	30	20	5	9	3
A2	10	30	7	5	7
A3	20	50	9	3	9
MAX	30	50	9	9	9
MIN	10	20	5	5	3

سپس اوزان نهایی را بر اساس مقادیر حداکثر و حداقل محاسبه می کنیم.

معیار / گزینه	C1	C2	C3	C4	C5
A1	0.333	0.4	0.556	1	0.333
A2	1	0.6	0.778	0.556	0.778
A3	0.5	1	1	0.333	1

(شاخص منفی) A11 = 10 /30 = 0.333

(شاخص مثبت) A21 = 20/50 = 0.4

مثال روش ساو مثال روش ساو مثال روش ساو