مدل برنامه ریزی فازی با ضرایب سمت راست فازی
مدل برنامه ریزی خطی فازی در حالی که فقط مقادیر سمت راست محدودیت ها اعداد فازی هستند (bi) به صورت ذیل است:
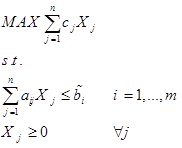
در حالت کلی مسئله برنامه ریزی خطی فازی ابتدا می بایست به یک مسئله معادل قطعی تبدیل شود و سپس با روش های استاندارد حل شده و جواب بهینه آن به دست آید. در نتیجه جواب نهایی مساله قطعی خواهد بود که با توجه به ساختار فازی مساله بدست آمده است.
مدل برنامه ریزی فازی با ضرایب سمت راست فازی مدل برنامه ریزی فازی با ضرایب سمت راست فازی مدل برنامه ریزی فازی با ضرایب سمت راست فازی
حال جهت تبدیل مدل برنامه ریزی خطی فازی به مدل قطعی فرض کنید تابع عضویت اعداد فازی سمت راست محدودیت ها به فرم ذیل باشد:
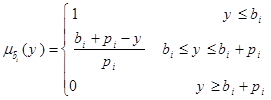
مدل برنامه ریزی فازی با ضرایب سمت راست فازی
برای هر بردار X=x1,x2,…,xn ابتدا درجه عضویت (Di(x که بیانگر درجه عضویت تامین محدودیت i توسط بردار X است، طبق رابطه ذیل محاسبه می شود:
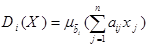
هر تابع Di(x) تشکیل یک مجموعه فازی در Rn می دهد که اشتراک آن ها منطقه موجه یا فضای جواب مسئله است. به دلیل فازی بودن فضای جواب مساله، تابع هدف نیز فازی می شود. لذا لازم است مجموعه فازی تابع هدف به دست آید. این کار با محاسبه حد پایین و بالا برای مقدار تابع هدف انجام می شود.
مدل برنامه ریزی فازی با ضرایب سمت راست فازی مدل برنامه ریزی فازی با ضرایب سمت راست فازی مدل برنامه ریزی فازی با ضرایب سمت راست فازی
حد پایین و بالا مقدار تابع هدف (Zi) با حل مسائل برنامه ریزی خطی ذیل بدست می آید.
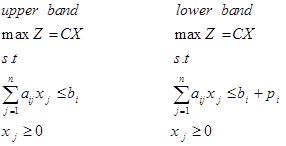
تابع عضویت مجموعه فازی مقادیر تابع هدف به صورت ذیل تعریف می شود:
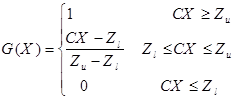
مدل برنامه ریزی فازی با ضرایب سمت راست فازی مدل برنامه ریزی فازی با ضرایب سمت راست فازی مدل برنامه ریزی فازی با ضرایب سمت راست فازی
حال جواب بهینه مساله با اشتراک تابع هدف و منطقه موجه و حداکثر کردن آن به دست می آید. برای اشتراک مجموعه های فازی تابع هدف و منطقه موجه از عملگر حداقل استفاده می نماییم.
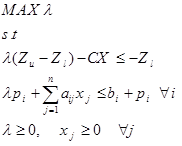
مثال مدل برنامه ریزی فازی با ضرایب سمت راست فازی
فرض کنید یک شرکت تولیدی دو محصول p1 و p2 تولید می کند. سود هر واحد از محصول p1 برابر 40 دلار و سود هر واحد از محصول p2 برابر 30 دلار است. تولید هر واحد محصول p1 دو برابر نفر ساعت مورد نیاز تولید هر واحد محصول p2 نیاز دارد.
کل نفر ساعت در دسترس در هر روز 500 نفر ساعت و این امکان وجود دارد که 100 نفر ساعت نیز به صورت اضافه کاری استفاده شود. میزان تولید اولیه در دسترس هر روز حداقل برای تولید400 واحد از محصولات p1 و p2 کافی است و طبق تجربه امکان افزایش تولید تا 500 واحد در روز وجود دارد.
حال مسئله به دنبال تعیین میزان تولید از محصولات p1 و p2 است به گونه ای که کل سود حداکثر شود. متغیرهای x1 و x2 برای میزان تولید محصول p1 و p2 در هر روز تعریف می شوند و مساله به فرم یک مدل برنامه ریزی خطی فازی به صورت زیر فرموله می شود:
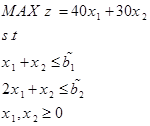
حال تابع عضویت اعداد فازی b1 و b2 به صورت زیر تعریف می شود:
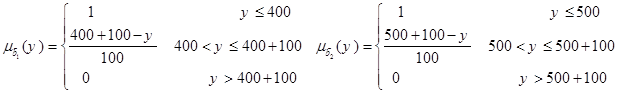
در ابتدا مقادیر Zu و Zl محاسبه می شود.
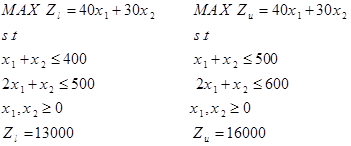
پس از آن در نهایت مساله برنامه ریزی فازی به صورت زیر بدست می آید:
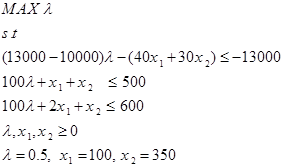
جواب بهینه: Z* = 40 (100) + 30 (350) = 14500
تصمیم گیری چند معیاره
تصمیمگیری شامل بیان درست اهداف، تعیین راهحلهای مختلف و ممکن، ارزیابی امکانپذیری آنان، ارزیابی عواقب و نتایج ناشی از اجرای هر یک از راهحلها و بالاخره انتخاب و اجرای آن میباشد. کیفیت مدیریت اساساً تابع کیفیت تصمیمگیری است زیرا کیفیت طرح و برنامهها، اثربخشی و کارآمدی راهبردها و کیفیت نتایجی که از اعمال آنها بدست میآید همگی تابع کیفیت تصمیماتی است که مدیر اتخاذ مینماید.
در اکثر موارد تصمیمگیریها وقتی مطلوب و مورد رضایت تصمیمگیرنده است که تصمیمگیری براساس چندین معیار مورد بررسی قرار گرفته باشد. معیارها ممکن است کمی یا کیفی باشند. در روشهای تصمیمگیری چند معیاره که در دهههای اخیر مورد توجه محققین قرار گرفتهاست به جای استفاده از یک معیار سنجش بهینگی از چند معیار سنجش استفاده میشود.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تص
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.
