مرتب سازی فازی
همان طور که مشاهده می شود در حالت تصادفی نمی توان به طور قطعی بر بزرگتربودن یک متغیر تصادفی نسبت به متغیر تصادفی دیگر حکم کرد و لذا احتمال بزرگتربودن آن محاسبه می شود.
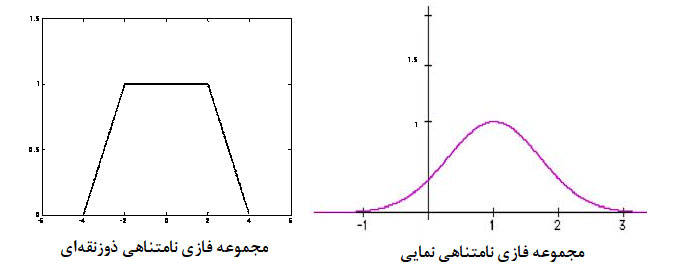
در حالت فازی نیز مانند حالت تصادفی نمی توان به طور قطعی در مقایسه دو عدد فازی حکم کرد ولی می توان میزان درستی یا صحت این که یک عدد فازی یک عدد فازی دیگر بزرگتر است را محاسبه کرد. میزان درستی و یا صحت بزرگتر بودن عدد فازی I از عدد فازی J به صورت زیر محاسبه می شود:
T (I > J) = sup x>=y min {µi(x), µj(y)}
بیشتر بدانیم
در حالت عمومی برای مقایسه K عدد فازی ، مشابه دو عدد فازی ذیل عمل می شود:
T(I>=I1,I2,…,IK)=T(I>=I1)AND T(I>=I2) AND… AND T (I>IK)
مثال مرتب سازی فازی
فرض کنید سه عدد فازی I, J, K به صورت ذیل باشد حال میزان صحت بزرگی I از J را محاسبه می کنیم.
I={1/3+0.85/7} J={0.7/4+1/6} K={0.8/2+1/4+0.5/8}
T (I>J) = MAX x1>=x2 {min (µi(x1), µj(x2))}
=MAX x1>=x2{min (µi(7),µj(4)), min(µi(7),µj(6))}
=MAX {min (0.8, 0.7), min (0.8, 1)}
=max {0.7, 0.8}
=0.8
T (I>=K) = 0.8
T (I>=J, K) = MIN {T (I>=J), T (I>=K)} = > MIN {0.8, 0.8} = 0.8
تصمیم گیری چند معیاره فازی
در تصمیم گیری شرایطی وجود دارد که جواب بهینه با درنظرگرفتن بیش از یک معیار می بایست تعیین گردد. یعنی فاکتورها و معیارهای مختلفی برای تعیین جواب بهینه لازم است بررسی گردند به این گونه موارد، مدل های تصمیم گیری چند معیاره گفته می شود که به دو طبقه عمده تقسیم می شود:
مرتب سازی فازی مرتب سازی فازی مرتب سازی فازی مرتب سازی فازی مرتب سازی فازی
- تصمیم گیری چند هدفه (MODM): بیشتر به منظور طراحی به کار گرفته می شوند و عمدتا یا مدل سازی ریاضی در فضای پیوسته همراه هستند.
- تصمیم گیری چند شاخصه(MADM): بیشتر برای انتخاب یک گزینه برتر در بین چندین گزینه کاندید و عمدتا با توجه به معیار های کیفی استفاده می شوند.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چند معیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.



