نظریه مجموعه های فازی
انسان علیرغم اطلاعات نادقیق و ناکافی در مواجه با مسایل پیچیده دنیای واقعی، رفتار و ماهیت سیستم را به طور تقریبی درک و تحلیل می نماید. حال سوال اصلی این است: آیا راهی وجود دارد که کامپیوتر نیز همانند انسان بتواند به طور تقریبی مسایل را با اطلاعات نادقیق و ناکافی درک و تحلیل نماید؟ برای پاسخ به این سوال، به اصل ناسازگاری پروفسور لطفی زاده که در سال 1973 مطرح گردید؛ توجه نمایید:
نظریه مجموعه های فازی
هر چه میزان آگاهی از یک سیستم افزایش یابد پیچیدگی سیستم کاهش یافته و دقت درک و تحلیل سیستم افزایش می یابد. زمانی که پیچیدگی سیستم کاهش یابد، دقت روش مدل سازی افزایش یافته و لذا ابزار مفیدی برای تحلیل سیستم مهیا می شود. ایده اصل ناسازگاری در شکل زیر به تصویر کشیده شده است.
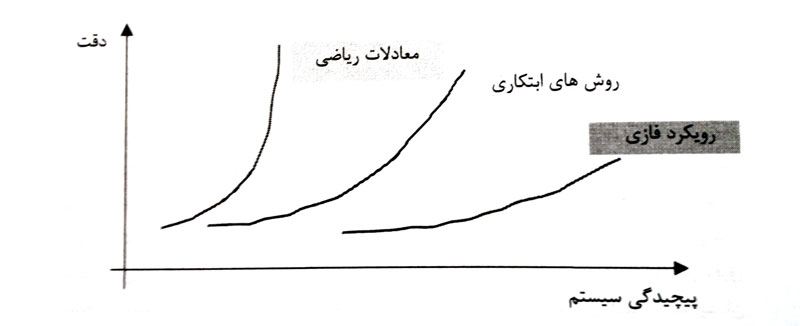
برای سیستم هایی که پیچیدگی آن ها کم و عدم قطعیت نیز ناچیز است می توان با استفاده از معادلات ریاضی ماهیت و رفتار سیستم را به طور دقیق مدل سازی و تحلیل کرد.
برای سیستم هایی که پیچیدگی آن ها کمی بیشتر است و عدم قطعیت نیز نسبتا زیاد است از روش های ابتکاری مدرن مانند شبکه عصبی و هوش مصنوعی استفاده می شود. در شبکه های عصبی به دلیل قابلیت یادگیری سیستم، عدم قطعیت به مرور کاهش یافته و قابلیت تحلیل موئر سیستم افزایش می یابد.
نظریه مجموعه های فازی
سر انجام برای سیستم های با پیچیدگی بالا و عدم قطعیت زیاد که اطلاعات کافی و دقیقی نیز در دسترس نیست رویکرد استدلال تقریبی فازی مطرح می شود که به سیستم های فازی معروف هستند. ورودی سیستم های فازی می توانند اطلاعات نادقیق (فازی) باشند و پردازش های سیستم نیز با بهره گیری از استدلال تقریبی و به طور فازی انجام شوند.
ایده نظریه مجموعه های فازی با این عبارت توسط پروفسور لطفی زاده مطرح شد: « ما نیازمند یک نوع دیگری از ریاضیات هستیم تا بتوانیم ابهامات و عدم دقت رویداد ها را مدل سازی نماییم، مدلی که متفاوت از نظریه احتمالات است.»
به عنوان مثال عبارت ” علی آدم تیزی است.” فازی نیست بلکه مبهم است. زیرا کلمه تیز می تواند با دو معنی برداشت شود : میزان سرعت عمل و میزان هوش، که در زبان محاوره برای هردو مفهوم کلمه “تیز” می تواند به کار رود. این حالت به معنی فازی بودن عبارت نیست بلکه عبارت کلامی ذکر شده مبهم است زیرا مشخص نیست که منظور شخص از بیان این عبارت، سرعت عکس العمل علی است یا میزان هوش علی. لذا در اینجا باید منظور مشخص شود تا ابهام رفع گردد.
نظریه مجموعه های فازی نظریه مجموعه های فازی نظریه مجموعه های فازی نظریه مجموعه های فازی نظریه مجموعه های فازی
فرض کنید به طور مثال در این عبارت منظور میزان هوش است، حال پس از رفع ابهام و مشخص شدن منظور مفهوم فازی مطرح می شود زیرا به طور دقیق مشخص نیست که در چه دامنه ای از میزان هوش ، شخص مورد نظر باهوش و کلمه تیز به ایشان اطلاق می شود.
سطح هوش مناسب برای انسان در مقیاس آی کیو در دامنه 100 الی 160 تعریف می شود حال این که مفهوم “تیز” در چه فاصله ای از این دامنه تعریف می شود و این که آیا می توان فاصله دقیقی برای هر یک از عبارا ت تعریف کرد به نظریه مجموعه های فازی مربوط است.
نظریه احتمال برای پیش بینی نتیجه یک رویداد تصادفی در آینده به کار می رود. رویدادی که در آینده قرار است اتفاق بیافتد و نتیجه آن در حال حاضر مشخص نیست. در واقع نظریه احتمال به رویدادهای اتفاقی مرتبط است. این در حالی است که فازی به ” بی دقتی” و مفاهیم نادقیق که در زبان طبیعی به کار می رود مرتبط است و همیشه با یک رویداد همراه نیست. در واقع نظریه فازی، عدم قطعیت غیر تصادفی را پشتیبانی می کند. این مفهوم در شکل زیر به تصویر کشیده شده است.
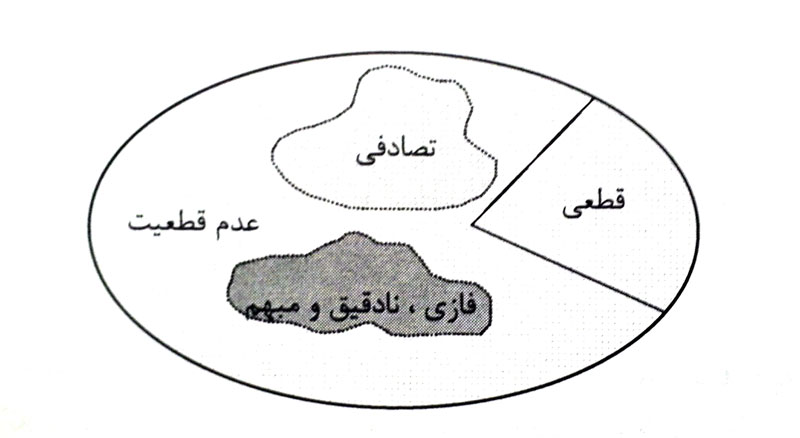
با این مقدمه کوتاه می توان چنین نتیجه گیری کرد: جاییکه پیچیدگی سیستم در حدی است که نمی توان با دقت و صراحت در مورد پارامترها، مشخصه ها و رفتار سیستم قضاوت کرد، مفهوم فازی جهت مدل سازی و تحلیل مطرح می شود. یک طبقه بندی عمومی از گستره نظریه فازی و کاربردهای آن به شرح زیر است:
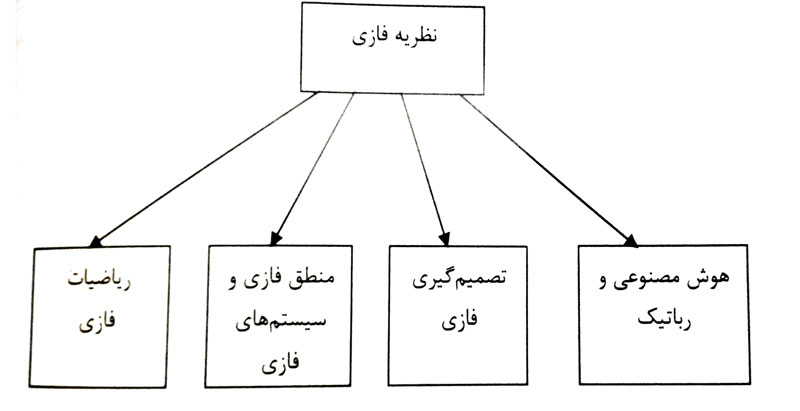
- ریاضیات فازی: شامل مجموعه های فازی و عملیات ریاضی مرتبط با آن ها است. در مجموعه های کلاسیک حد و مرز مجموعه به طور دقیق و قطعی تعریف می شود و در نتیجه عضویت عناصر در مجموعه نیز به طور قطعی مشخص می شود. در مجموعه های کلاسیک یک عنصر قطعا عضو مجموعه هست یا قطعا عضو آن نیست. اما در عمل موارد بسیاری وجود دارد که تعریف حد و مرز دقیق و قطعی برای مجموعه امکان پذیر نیست. به عنوان مثال برای مجموعه افراد چاق نمی توان حد و مرز مشخصی تعریف کرد ، زیرا به طور دقیق نمی توان بر چاق بودن و یا نبودن یک شخص قضاوت کرد. لذا نیاز به مجموعه ای داریم که محدوده آن منعطف و به طور تقریبی (نا دقیق) تعریف شود. به این نوع مجموعه، مجموعه فازی گفته می شود. عضویت عناصر در مجموعه های فازی نیز با درجه عضویت که عددی بین صفر و یک است بیان می شود.
- منطق فازی: در واقع تکامل یافته منطق کلایسک است.در منطق کلاسیک که منطقی دو ارزشی است یک گزاره می تواند درست یا نادرست باشد. در حالی که در منطق فازی منطق چند ارزشی است و ارزش درستی هر گزاره می تواند عددی بین صفر تا یک باشد.
- سیستم های فازی: سیستم هایی هستند که اطلاعات ورودی آن ها می تواند به صورت نادقیق باشد یعنی اطلاعات ورودی یک سیستم فازی به صورت مجموعه هایی فازی یا اعداد فازی خواهند بود. از طرفی دیگر پردازش های یک سیستم فازی می تواند به صورت نادقیق انجام شود. یکی از معروف ترین و کاربردی ترین پردازش های نادقیق در سیستم های فازی استفاده از پایگاه قوانین فازی است. در پایگاه قوانین فازی هر قانون با ساختار “اگر- آن گاه” تعریف می شود.
- تصمیم گیری فازی: حالت عمومی شده تصمیم گیری کلاسیک است. در تصمیم گیری کلاسیک، تصمیم بهینه از بین تصمیم های ممکن در مواجهه با محدودیت های مسئله و با هدف بهینه کردن تابع مطلوبیت بدست می آید.تابع مطلوبیت، پارامترهاو محدودیت ها در تصمیم گیری کلاسیک، قطعی و دقیق فرض می شوند در حالی که در تصمیم گیری فازی امکان تعریف نادقیق و تقریبی پارامترها ، تابع مطلوبیت و محدودیت های مساله وجود دارد.
- هوش مصنوعی و رباتیک: با بهره گیری از نظریه فازی در طراحی ربات ها هوشمند امکان کسب اطلاعات دنیای واقعی توسط ربات ها ایجاد شده و همین طور تحلیل و پردازش فازی امکان عمل و عکس العمل مشابه انسان را به ربات ها می دهد.
نظریه مجموعه های فازی نظریه مجموعه های فازی نظریه مجموعه های فازی نظریه مجموعه های فازی نظریه مجموعه های فازی
در ادامه بخوانید
تصمیم گیری چند معیاره
تصمیمگیری شامل بیان درست اهداف، تعیین راهحلهای مختلف و ممکن، ارزیابی امکانپذیری آنان، ارزیابی عواقب و نتایج ناشی از اجرای هر یک از راهحلها و بالاخره انتخاب و اجرای آن میباشد. کیفیت مدیریت اساساً تابع کیفیت تصمیمگیری است زیرا کیفیت طرح و برنامهها، اثربخشی و کارآمدی راهبردها و کیفیت نتایجی که از اعمال آنها بدست میآید همگی تابع کیفیت تصمیماتی است که مدیر اتخاذ مینماید.
در اکثر موارد تصمیمگیریها وقتی مطلوب و مورد رضایت تصمیمگیرنده است که تصمیمگیری براساس چندین معیار مورد بررسی قرار گرفته باشد. معیارها ممکن است کمی یا کیفی باشند. در روشهای تصمیمگیری چند معیاره که در دهههای اخیر مورد توجه محققین قرار گرفتهاست به جای استفاده از یک معیار سنجش بهینگی از چند معیار سنجش استفاده میشود.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تص
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.
