آموزش جامع روش ARAS فازی
در دنیای پیچیده تصمیمگیری چندمعیاره (MCDM)، روش ARAS فازی که مخفف Additive Ratio Assessment است، به عنوان یکی از دقیقترین ابزارها برای سنجش «درجه بهینگی» گزینهها شناخته میشود. این روش که اولین بار توسط زوادسکاس و تورسکیس در سال ۲۰۱۰ معرفی شد، بر این منطق استوار است که پدیدههای دنیای واقعی را میتوان از طریق مقایسه با یک «گزینه ایدئال فرضی» بهتر درک کرد. برخلاف بسیاری از روشها که فقط به رتبهبندی اکتفا میکنند، روش ARAS فازی به شما میگوید که هر گزینه چقدر به حالت بهینه مطلق نزدیک است.
تفاوت بنیادین این روش با متدهایی مثل روش TOPSIS فازی در این است که ARAS به جای تمرکز بر فواصل هندسی، بر روی «نسبت سودمندی» تمرکز دارد. در واقع، این روش مجموع مقادیر نرمالشده و وزین هر گزینه را با مجموع مقادیر گزینه بهینه مقایسه میکند. ورود منطق فازی به این ساختار، به تصمیمگیرنده اجازه میدهد تا ابهامات موجود در نظرات کارشناسان را که معمولاً با عبارات کلامی (مثل “بسیار زیاد” یا “متوسط”) بیان میشوند، با دقت ریاضی بالایی در قالب اعداد فازی مثلثی مدلسازی کند.
آنچه می خوانید
فلسفه رتبهبندی با روش ARAS فازی
در سال ۲۰۲۶، روش ARAS فازی به دلیل ساختار سلسلهمراتبی و توانایی در ارائه تحلیلهای کمی دقیق، به یکی از محبوبترین روشها در مقالات علمی و پایاننامههای مهندسی صنایع و مدیریت تبدیل شده است. این روش نه تنها گزینهها را ردیف میکند، بلکه با ارائه شاخص K_i (درجه بهینگی)، یک معیارِ درصدی از کارایی هر گزینه به مدیران میدهد. این ویژگی باعث میشود که روش ARAS فازی مکمل بسیار خوبی برای روشهای وزندهی نظیر روش BWM فازی باشد.
پذیرش این روش در محیطهای آکادمیک به دلیل سادگی در درک و در عین حال، عمقِ تحلیلی آن است. زمانی که دادهها ناقص یا دارای ابهام هستند، روش ARAS فازی با استفاده از عملگرهای فازی، پایداری نتایج را تضمین میکند. این روش به ویژه زمانی که هدف، انتخاب بهترین گزینه از میان مجموعهای از جایگزینهای نزدیک به هم است، قدرت تفکیک بسیار بالایی از خود نشان میدهد و از “خطای رتبهبندی” که در روشهای سادهتر ممکن است رخ دهد، جلوگیری میکند.
مزایای روش ARAS فازی: چرا حرفهایها از آن استفاده میکنند؟
یکی از بزرگترین مزایای روش ARAS فازی، تعریف گزینه بهینه فرضی (A_0) است. در این روش، ما یک گزینه ایدئال را بر اساس بهترین مقادیر موجود در ماتریس تصمیم خلق میکنیم. این کار باعث میشود که رتبهبندی نهایی نه فقط یک مقایسه بین گزینههای موجود، بلکه یک مقایسه با «بهترین حالت ممکن» باشد. این ویژگی در روشهایی مثل [روش SAW فازی] دیده نمیشود و باعث افزایش واقعگرایی در نتایج میشود.
مزیت دوم، سادگی در محاسبات و تفسیر نتایج است. علیرغم استفاده از منطق فازی، فرآیند تجمیع در این روش بر پایه جمع ساده وزین (Additive) است که درک آن را برای مدیران ارشد سازمان که دانش ریاضی عمیقی ندارند، آسان میکند. خروجی نهایی که یک عدد بین ۰ و ۱ است، به سادگی به عنوان “درصد کارایی” قابل تعبیر است. برای مثال، اگر درجه بهینگی گزینهای ۰.۸۵ باشد، یعنی این گزینه ۸۵٪ به حالت ایدئال نزدیک است؛ این شفافیت در روش روش VIKOR فازی کمتر به چشم میخورد.
همچنین، ARAS فازی در مواجهه با معیارهای متضاد (سود و هزینه) بسیار منعطف عمل میکند. فرآیند نرمالسازی در این روش به گونهای طراحی شده که ماهیت معکوس معیارهای هزینه را به خوبی به مقادیر سود تبدیل میکند، بدون اینکه تناسب مقادیر فازی از بین برود. این پایداری در نرمالسازی باعث میشود که رتبهبندی نهایی نسبت به تغییرات جزئی در دادههای ورودی حساسیت منطقی داشته باشد و از “پرش رتبه” جلوگیری کند.
در نهایت، قابلیت ترکیب این روش با سایر تکنیکهای مدرن MCDM یک مزیت رقابتی برای پژوهشگران است. امروزه بسیاری از متخصصان از روش ARAS فازی در کنار روشهای وزندهی عینی مثل روش MEREC فازی استفاده میکنند تا سوگیریهای احتمالی خبرگان را به حداقل برسانند. این سطح از انعطافپذیری باعث شده تا ARAS فازی در اکثر پلتفرمهای تحلیل تصمیمگیری به عنوان یک ماژول استاندارد گنجانده شود.
معایب و محدودیتهای روش ARAS فازی
با وجود تمام نقاط قوت، روش ARAS فازی بدون چالش نیست. بزرگترین محدودیت این روش، وابستگی شدید به گزینه بهینه (A_0) است. اگر در یک معیار خاص، مقدار یکی از گزینهها بسیار دورتر از بقیه باشد (داده پرت)، گزینه بهینه بر اساس آن شکل میگیرد و این موضوع میتواند باعث شود که درجه بهینگی سایر گزینهها به شدت افت کند و تحلیل را دچار انحراف نماید. بنابراین، پیشپردازش دادهها و اطمینان از صحت مقادیر ماتریس تصمیم در این روش حیاتیتر از روشهایی مثل روش PROMETHEE فازی است.
چالش دوم در مرحله دیفازیسازی نهفته است. از آنجایی که ARAS فازی با اعداد فازی مثلثی کار میکند، در گام نهایی باید امتیازات را به عدد قطعی تبدیل کرد. انتخاب روش دیفازیسازی (مانند مرکز ثقل یا بزرگترین کران) میتواند تاثیر جزئی بر رتبههای نزدیک به هم داشته باشد. این موضوع باعث میشود که برخی داوران مقالات علمی، انجام تحلیل حساسیت بر روی روشهای دیفازیسازی را از پژوهشگر مطالبه کنند که حجم کار را افزایش میدهد.

همچنین، این روش به تنهایی راهکاری برای تعیین وزن معیارها ارائه نمیدهد. ARAS فازی یک روش رتبهبندی محض است و به شدت به وزنهای ورودی وابسته است. اگر وزنهای اختصاص یافته به معیارها (که معمولاً از روشهایی مثل [روش AHP فازی] استخراج میشوند) دارای نرخ ناسازگاری بالایی باشند، خروجی ARAS فازی نیز بیاعتبار خواهد بود. این عدم استقلال محاسباتی باعث میشود که کاربر مجبور به یادگیری و اجرای حداقل دو روش MCDM متفاوت باشد.
در نهایت، بار محاسباتی در مسائل بزرگ میتواند خستهکننده باشد. زمانی که تعداد گزینهها و معیارها از حد خاصی فراتر میرود، محاسبه دستی روابط نرمالسازی و تجمیع فازی برای تکتک سلولها احتمال خطای انسانی را بالا میبرد. به همین دلیل، استفاده از ابزارهای کمکی مثل اکسل آماده ARAS فازی برای اطمینان از صحت نتایج در پروژههای صنعتی و دانشگاهی، نه یک انتخاب، بلکه یک ضرورت محسوب میشود.
کاربردهای گسترده روش ARAS فازی در صنعت و خدمات
روش ARAS فازی در حوزههای متنوعی که نیاز به ارزیابی دقیق عملکرد دارند، نفوذ کرده است. یکی از اصلیترین کاربردها، ارزیابی و انتخاب تأمینکننده در زنجیره تأمین است. به دلیل توانایی این روش در مدلسازی معیارهای کیفی مثل “قابلیت اطمینان” و “مسئولیت اجتماعی” در کنار معیارهای کمی مثل “قیمت”، شرکتهای بزرگ از ARAS فازی برای رتبهبندی شرکای تجاری خود استفاده میکنند تا ریسکهای زنجیره تأمین را به حداقل برسانند.
در حوزه مهندسی عمران و مدیریت پروژه، این روش برای انتخاب بهینهترین مصالح یا روشهای ساختوساز به کار میرود. برای مثال، زمانی که یک مهندس با چندین گزینه برای سیستم سقف روبرو است و معیارهایی مثل هزینه، سرعت اجرا، مقاومت در برابر زلزله و عایقبندی را در نظر دارد، روش ARAS فازی با تعیین درجه بهینگی، به او کمک میکند تا گزینهای را انتخاب کند که بهترین توازن را بین الزامات فنی و بودجهای برقرار سازد. این کاربرد شباهت زیادی به کاربردهای [روش WASPAS فازی] دارد.
همچنین در بخش بهداشت و درمان، برای رتبهبندی بیمارستانها یا انتخاب بهترین استراتژی درمانی استفاده میشود. از آنجایی که در پزشکی با ابهامات زیادی در تشخیص و نتایج روبرو هستیم، ماهیت فازی ARAS اجازه میدهد تا نظرات تیمهای مختلف پزشکی به درستی تلفیق شده و عادلانهترین رتبهبندی ارائه گردد. پایداری این روش در محیطهای پرریسک، آن را به ابزاری قابل اعتماد برای مدیران بخش سلامت تبدیل کرده است.
در سطح کلان مدیریتی، ARAS فازی برای ارزیابی عملکرد شعب بانکها یا مناطق شهرداری نیز به کار میرود. با استفاده از این روش، مدیران ارشد میتوانند بفهمند که هر شعبه نسبت به “شعبه ایدئال” در چه وضعیتی قرار دارد. این تحلیلِ درصدی، انگیزهای برای بهبود عملکرد شعب ضعیفتر ایجاد میکند و مبنای علمی دقیقی برای تخصیص پاداش و منابع فراهم میآورد.
گامهای اجرایی و الگوریتم محاسباتی روش ARAS فازی
اجرای روش ARAS در محیط فازی یک فرآیند منضبط است که از تعیین گزینهی ایدئال شروع شده و به محاسبه نسبت سودمندی ختم میشود. اولین گام در این مسیر، تشکیل ماتریس تصمیم فازی و تعیین گزینه بهینه (A_0) است. برای این کار، اگر معیار از نوع مثبت (سود) باشد، بیشترین مقدار فازی در آن ستون و اگر از نوع منفی (هزینه) باشد، کمترین مقدار فازی به عنوان مقدارِ A_0 در نظر گرفته میشود. این گزینه فرضی، به عنوان خطکش و معیارِ سنجش تمام گزینههای دیگر در طول فرآیند عمل میکند.
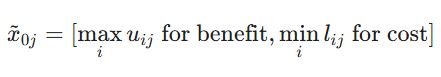
پس از تشکیل ماتریس بسطیافته (که شامل A_0 است)، نوبت به نرمالسازی فازی میرسد. در روش ARAS فازی، فرآیند نرمالسازی برای معیارهای سود و هزینه متفاوت است. برای معیارهای مثبت، هر درایه بر مجموع مقادیر آن ستون تقسیم میشود. برای معیارهای هزینه، ابتدا معکوس مقادیر فازی محاسبه شده و سپس فرآیند تقسیم انجام میگیرد. هدف از این گام، بیمقیاس کردن اعداد و آمادهسازی آنها برای ترکیب با وزن معیارهاست، به طوری که تمام مقادیر در بازه [0, 1] قرار گیرند و قابلیت مقایسه داشته باشند.

در گام سوم، وزندهی و تجمیع انجام میشود. در این مرحله، مقادیر نرمالشده در وزن اختصاصی هر معیار (w_j) ضرب میشوند تا ماتریس وزین فازی شکل بگیرد. وزنها معمولاً از روشهای دقیقتری مثل روش BWM فازی استخراج میشوند تا نتایج نهایی اعتبار علمی بالایی داشته باشند. پس از وزندهی، مجموع مقادیر وزین برای هر گزینه (شامل گزینه بهینه) محاسبه میشود که آن را با نماد Si نشان میدهیم. این شاخص در واقع «ارزش عملکردی» هر گزینه را در محیط فازی نشان میدهد.
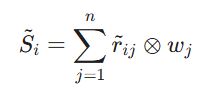
آخرین گام، محاسبه درجه بهینگی (K_i) و رتبهبندی است. پس از دیفازیسازی مقادیر S_i (معمولاً به روش مرکز ثقل)، درجه بهینگی هر گزینه از تقسیم امتیاز آن گزینه بر امتیاز گزینه بهینه (S_0) به دست میآید. عددی که حاصل میشود، نشاندهنده درصد نزدیکی آن گزینه به حالت ایدئال است. هرچه K_i به عدد ۱ نزدیکتر باشد، آن گزینه اولویت بالاتری دارد. این روش برخلاف روش TOPSIS فازی که بر فواصل تمرکز دارد، بر پایه نسبت کارایی استوار است.
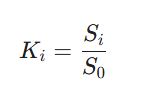
مثال عددی: انتخاب بهترین آژانس تبلیغاتی
برای درک بهتر، یک مسئله تصمیمگیری با ۴ گزینه (A_1, A_2, A_3, A_4) و ۳ معیار را در نظر میگیریم:
- هزینه (C_1): وزن ۰.۴ (جنبه منفی/هزینه)
- خلاقیت (C_2): وزن ۰.۳۵ (جنبه مثبت/سود)
- سابقه کار (C_3): وزن ۰.۲۵ (جنبه مثبت/سود)
گام اول: تشکیل ماتریس تصمیم فازی (امتیازات از ۱ تا ۹)
ابتدا گزینه A_0 را بر اساس بهترین مقادیر (کمترین برای هزینه و بیشترین برای بقیه) تشکیل میدهیم:
| گزینهها | C1 (Min) | C2 (Max) | C3 (Max) |
| A0 (بهینه) | (2, 2, 3) | (7, 9, 9) | (8, 9, 9) |
| A1 | (4, 5, 6) | (5, 7, 8) | (6, 7, 8) |
| A2 | (2, 3, 4) | (6, 8, 9) | (5, 6, 7) |
| A3 | (5, 6, 7) | (7, 8, 9) | (7, 8, 9) |
| A4 | (3, 4, 5) | (4, 5, 6) | (4, 5, 6) |
گام دوم: نرمالسازی و وزندهی
در این مرحله، مقادیر هزینه معکوس شده و سپس تمام ستونها به گونهای نرمال میشوند که جمع درایههای هر ستون برابر با عدد فازی واحد شود. سپس وزن معیارها (w_j) در درایهها ضرب میشود. برای مثال در معیار C_2، تمام امتیازات بر مجموع امتیازات آن ستون تقسیم شده و در ۰.۳۵ ضرب میشوند.
گام سوم: محاسبه S_i و درجه بهینگی (K_i)
پس از جمع زدن مقادیر وزین در هر سطر و دیفازیسازی، نتایج فرضی زیر حاصل میشود:
- S0: 0.880 ایده آل
- S1: 0.642 -> K1: 0.73
- S2: 0.792-> K2: 0.90
- S3: 0.704->K3: 0.80
- S4: 0.528->K4: 0.60
رتبهبندی نهایی:
بر اساس مقادیر K_i، رتبهبندی گزینهها به صورت A_2 > A_3 > A_1 > A_4 است. گزینه A_2 با درجه بهینگی 90%، بهترین انتخاب سازشی است. این دقت در رتبهبندی، مشابه خروجیهای روش روش VIKOR فازی است اما با تمرکز بر نسبت کارایی.
گام نهایی برای شما:
اکنون که با تمامی ابعاد روش ARAS فازی آشنا شدید، زمان آن رسیده که پروژه خود را با دقتی حرفهای به پایان برسانید. پیشنهاد میکنیم با تهیه پکیج اکسل ARAS فازی از فروشگاه فرابگیر، محاسبات پیچیده خود را خودکارسازی کنید. همچنین اگر در مرحله انتخاب روش وزندهی هستید، حتماً مقاله آموزش روش BWM فازی را مطالعه فرمایید.
نتیجهگیری: ARAS فازی، ابزاری برای سنجش تعالی
روش ARAS فازی اثبات کرده است که در دنیای رقابتی امروز، صرفاً «برنده بودن» کافی نیست، بلکه باید دانست «چقدر با وضعیت مطلوب فاصله داریم». این روش با معرفی شاخص درجه بهینگی، یک معیارِ بنچمارک (Benchmark) در اختیار مدیران قرار میدهد تا نه تنها گزینهها را اولویتبندی کنند، بلکه پتانسیل بهبود هر گزینه را نیز شناسایی نمایند. این رویکرد تحلیلی، ARAS را به یکی از ارکان تصمیمگیری راهبردی تبدیل کرده است.
استفاده از این متد در کنار روشهای نوین وزندهی مثل روش MEREC فازی، سوگیریهای انسانی را به حداقل رسانده و نتایجی کاملاً مستدل ارائه میدهد. پایداری ریاضی این روش در محیطهای فازی، اطمینان خاطری برای پژوهشگران است تا در مقالات ISI خود از متدی استفاده کنند که هم از نظر تئوری غنی است و هم از نظر اجرایی، شفافیت بالایی دارد.
در نهایت، موفقیت در به کارگیری ARAS فازی به دقت در فرمولنویسی و پیادهسازی گامهای نرمالسازی بستگی دارد. با توجه به حجم بالای مقایسات در این روش، توصیه میشود برای پروژههای حساس از ابزارهای استانداردی مانند اکسل آماده ARAS فازی استفاده کنید. این کار به شما اجازه میدهد به جای درگیری با خطاهای محاسباتی، بر روی تحلیل استراتژیک خروجیها و نگارش بخشهای کیفی پژوهش خود تمرکز کنید.
سوالات متداول درباره روش ARAS فازی
تفاوت اصلی ARAS با روشهای مشابه مثل SAW چیست؟
تفاوت کلیدی در تعریف «گزینه بهینه (A_0)» است. در حالی که روش [روش SAW فازی] صرفاً به جمع وزین امتیازات اکتفا میکند، ARAS نتایج را نسبت به یک حدِ بهینگی میسنجد. این کار باعث میشود خروجی ARAS (درجه بهینگی) معنای ملموستری داشته باشد؛ چرا که به شما میگوید گزینه منتخب چند درصد از ایدئالِ مطلق را پوشش داده است، در حالی که SAW فقط یک امتیاز نسبی ارائه میدهد.
آیا میتوان از ARAS فازی برای تعداد گزینههای بسیار زیاد استفاده کرد؟
بله؛ یکی از محاسن ARAS فازی این است که برخلاف روشهایی مثل [روش AHP فازی]، با افزایش تعداد گزینهها دچار «انفجار مقایسات» نمیشود. بار محاسباتی در این روش به صورت خطی رشد میکند، لذا برای رتبهبندیهای با حجم دیتای بالا بسیار مناسب است. البته در چنین مواردی، استفاده از فایل اکسل ARAS فازی برای جلوگیری از خطاهای انسانی در عملیات جمع و تقسیم فازی، شدیداً توصیه میشود.
چرا رتبه اول در ARAS ممکن است با TOPSIS متفاوت باشد؟
این موضوع به دلیل «منطق فاصله» در مقابل «منطق نسبت» است. تاپسیس به دنبال گزینهای است که کمترین فاصله اقلیدسی را از ایدئال داشته باشد، اما ARAS به دنبال بالاترین نسبت سودمندی است. در مسائلی که توزیع امتیازات غیریکنواخت است، ARAS معمولاً نتایج واقعبینانهتری ارائه میدهد چون به جای فواصل هندسی، بر روی مجموع ارزش عملکردی تمرکز دارد. برای اعتبارسنجی بیشتر، پیشنهاد میشود نتایج را با روش CoCoSo فازی نیز چک کنید.
