مسائل تصمیم گیری چندمعیاره (MCDM) در دنیای واقعی، با چالشهای متعددی همراه هستند. از جمله این چالشها میتوان به ابهام و عدم قطعیت در اطلاعات، معیارها و ترجیحات تصمیم گیرندگان اشاره کرد. برای غلبه بر این چالشها، روشهای مختلفی مبتنی بر تئوری فازی ارائه شدهاند. دو روش محبوب در این میان، AHP فازی و TOPSIS فازی هستند.

در این مقاله، روش ترکیبی Fuzzy AHP و Fuzzy Topsis ارائه میشود که مزایای هر دو روش را به طور همزمان به کار میگیرد. روش TOPSIS-AHP فازی ، ابزاری قدرتمند برای حل مسائل MCDM در شرایطی است که اطلاعات و ترجیحات تصمیم گیرندگان با ابهام و عدم قطعیت همراه باشند.
آنچه می خوانید
تئوری فازی
تئوری فازی، ابزاری قدرتمند برای مدلسازی و تحلیل اطلاعات و مفاهیم نامشخص و مبهم است. برخلاف منطق کلاسیک که در آن همه چیز یا درست است یا غلط، تئوری فازی به ما امکان میدهد تا با درجات مختلف صحت و درستی کار کنیم. این امر تئوری فازی را به ابزاری ایدهآل برای حل مسائلی تبدیل میکند که با ابهام و عدم قطعیت همراه هستند، مانند:
- تصمیم گیری: انتخاب بهترین گزینه از بین چندین گزینه با معیارهای متعدد و اغلب نامشخص
- تشخیص: دستهبندی دادهها یا تشخیص الگوها در شرایطی که اطلاعات کامل و دقیقی در دسترس نیست
- کنترل: کنترل سیستمهای پیچیده با استفاده از قوانین و استدلالهای فازی
مفاهیم کلیدی در تئوری فازی
- مجموعههای فازی: برخلاف مجموعههای کلاسیک که اعضای آنها فقط میتوانند دو مقدار “متعلق به مجموعه” یا “متعلق به مجموعه نیست” را داشته باشند، در مجموعههای فازی، درجه تعلق هر عضو به مجموعه با یک عدد فازی بین 0 و 1 نشان داده میشود.
- اعداد فازی: اعداد فازی، اعدادی هستند که مقادیر دقیق را به همراه درجه عدم قطعیت آنها نشان میدهند. برای مثال، عدد فازی (3، 4، 5) نشان میدهد که مقدار مورد نظر بین 3 و 5 است و به احتمال بیشتر به 4 نزدیک است.
- منطق فازی: منطق فازی، قواعدی برای استدلال و نتیجهگیری با استفاده از اعداد و مفاهیم فازی ارائه میدهد.
مزایای استفاده از تئوری فازی
- قابلیت مدلسازی دنیای واقعی: تئوری فازی به ما امکان میدهد تا دنیای واقعی را که اغلب با ابهام و عدم قطعیت همراه است، به طور دقیقتر مدلسازی کنیم.
- افزایش قدرت تصمیم گیری: با استفاده از تئوری فازی، میتوانیم در شرایطی که اطلاعات کامل و دقیقی در دسترس نیست، تصمیمات بهتری بگیریم.
- کاهش پیچیدگی: تئوری فازی میتواند به سادهسازی مسائل پیچیده و تسهیل حل آنها کمک کند.
کاربردهای تئوری فازی
- سیستمهای کنترل: کنترل ماشینهای لباسشویی، دوربینهای دیجیتال، و رباتها
- سیستمهای تشخیص: تشخیص تقلب، تشخیص پزشکی، و تشخیص عیوب
- سیستمهای پشتیبانی تصمیم: انتخاب سبد سرمایهگذاری، انتخاب محل احداث تأسیسات، و انتخاب بهترین روش درمانی
- سیستمهای پردازش تصویر: فشردهسازی تصویر، بازیابی تصویر، و تشخیص چهره
روش AHP فازی
فرآیند تحلیل سلسله مراتبی فازی (AHP فازی) روشی نوین برای حل مسائل تصمیم گیری چندمعیاره (MCDM) در شرایطی است که اطلاعات و ترجیحات با ابهام و عدم قطعیت همراه باشند. این روش، از مزایای تئوری فازی برای غلبه بر این چالشها و ارائه راهحلی منطقی و قابل توجیه برای مسائل MCDM استفاده میکند.
مراحل کلی AHP فازی
- شناسایی معیارها و گزینهها: اولین قدم در AHP فازی، شناسایی معیارهایی است که برای ارزیابی گزینهها به کار میروند. همچنین، باید تمام گزینههای جایگزین که در نظر گرفته میشوند، مشخص شوند.
- ساختار سلسله مراتبی: در این مرحله، معیارها در یک ساختار سلسله مراتبی سازماندهی میشوند. این ساختار باید به گونهای باشد که معیارهای کلیتر در سطوح بالاتر و معیارهای جزئیتر در سطوح پایینتر قرار بگیرند.
- تعیین اوزان معیارها: در این مرحله، از مقایسات زوجی برای تعیین اهمیت نسبی هر معیار نسبت به معیارهای دیگر در همان سطح استفاده میشود. برای انجام مقایسات زوجی، از اعداد فازی استفاده میشود.
- ارزیابی گزینهها: در این مرحله، هر گزینه با توجه به هر معیار ارزیابی میشود. برای این کار، از مقایسات زوجی بین گزینهها با توجه به هر معیار استفاده میشود. مانند مرحله قبل، در این مقایسات نیز از اعداد فازی استفاده میشود.
- محاسبه وزن نهایی هر گزینه: با استفاده از اوزان معیارها و مقادیر ارزیابی گزینهها، وزن نهایی هر گزینه محاسبه میشود.
- رتبهبندی گزینهها: بر اساس وزن نهایی هر گزینه، گزینهها رتبهبندی میشوند و بهترین گزینه انتخاب میشود.
روش TOPSIS فازی
تکنیک TOPSIS فازی (Technique for Order Preference by Similarity to Ideal Solution) روشی نوین برای حل مسائل تصمیم گیری چندمعیاره (MCDM) در شرایطی است که اطلاعات و ترجیحات با ابهام و عدم قطعیت همراه باشند. این روش، از مزایای تئوری فازی برای غلبه بر این چالشها و ارائه راهحلی منطقی و قابل توجیه برای مسائل MCDM استفاده میکند.
مراحل کلی TOPSIS فازی
- شناسایی معیارها و گزینهها: اولین قدم در TOPSIS فازی، شناسایی معیارهایی است که برای ارزیابی گزینهها به کار میروند. همچنین، باید تمام گزینههای جایگزین که در نظر گرفته میشوند، مشخص شوند.
- ایجاد ماتریس تصمیم: در این مرحله، ماتریسی از مقادیر ارزیابی گزینهها با توجه به هر معیار ایجاد میشود. در TOPSIS فازی، از اعداد فازی برای نشان دادن مقادیر ارزیابی استفاده میشود.
- محاسبه مقادیر ایدهآل مثبت و منفی: در این مرحله، مقادیر ایدهآل مثبت و منفی برای هر معیار محاسبه میشود. مقادیر ایدهآل مثبت، بهترین مقادیر ممکن برای هر معیار هستند، در حالی که مقادیر ایدهآل منفی، بدترین مقادیر ممکن برای هر معیار هستند.
- محاسبه فاصله هر گزینه از مقادیر ایدهآل: در این مرحله، فاصله هر گزینه از مقادیر ایدهآل مثبت و منفی برای هر معیار محاسبه میشود. برای محاسبه این فواصل، از فاصلههای فازی استفاده میشود.
- محاسبه شاخص شباهت به راه حل ایدهآل: در این مرحله، شاخص شباهت هر گزینه به راهحل ایدهآل (S) و شاخص شباهت هر گزینه به راهحل ضد ایدهآل (NS) محاسبه میشود.
- رتبهبندی گزینهها: بر اساس مقادیر S و NS، گزینهها رتبهبندی میشوند و بهترین گزینه انتخاب میشود.
روش TOPSIS-AHP فازی
روش ترکیبی روش TOPSIS-AHP فازی، روشی نوین و کارآمد برای حل مسائل تصمیم گیری چندمعیاره (MCDM) در شرایطی است که اطلاعات و ترجیحات با ابهام و عدم قطعیت همراه باشند. این روش، از مزایای هر دو روش AHP فازی و TOPSIS فازی به طور همزمان استفاده میکند و ابزاری قدرتمند برای تصمیم گیری منطقی و قابل توجیه در شرایط پیچیده و مبهم فراهم میکند.
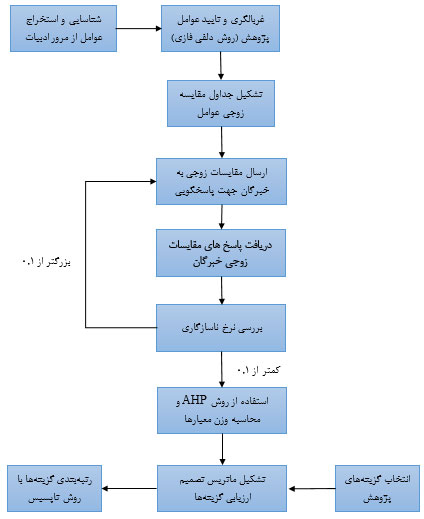
مراحل کلی روش ترکیبی روش TOPSIS-AHP فازی
شناسایی معیارها و گزینهها: اولین قدم، شناسایی معیارهایی است که برای ارزیابی گزینهها به کار میروند. همچنین، باید تمام گزینههای جایگزین که در نظر گرفته میشوند، مشخص شوند.

تعیین اوزان معیارها با استفاده از AHP فازی: در این مرحله، از AHP فازی برای تعیین اهمیت نسبی هر معیار نسبت به معیارهای دیگر در همان سطح استفاده میشود. برای این کار، از مقایسات زوجی بین معیارها با استفاده از اعداد فازی استفاده میشود.
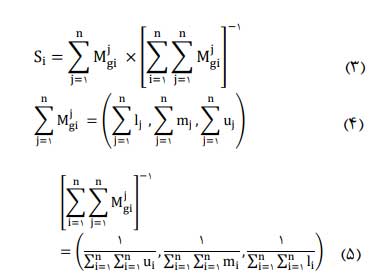
ارزیابی گزینهها با استفاده از TOPSIS فازی: در این مرحله، هر گزینه با توجه به هر معیار با استفاده از TOPSIS فازی ارزیابی میشود. برای این کار، از مقایسات زوجی بین گزینهها با توجه به هر معیار و محاسبه فواصل فازی از مقادیر ایدهآل استفاده میشود.

محاسبه وزن نهایی هر گزینه: با استفاده از اوزان معیارها و مقادیر ارزیابی گزینهها که از TOPSIS فازی به دست آمدهاند، وزن نهایی هر گزینه محاسبه میشود.
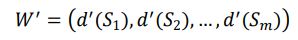
رتبهبندی گزینهها: بر اساس وزن نهایی هر گزینه، گزینهها رتبهبندی میشوند و بهترین گزینه انتخاب میشود.

مزایای روش ترکیبی روش TOPSIS-AHP فازی
- قابلیت مدلسازی دقیقتر ابهام و عدم قطعیت: این روش از مزایای هر دو روش AHP فازی و TOPSIS فازی برای مدلسازی دقیقتر ابهام و عدم قطعیت موجود در اطلاعات و ترجیحات تصمیم گیرندگان استفاده میکند.
- استفاده کامل از دانش و تجربیات تصمیم گیرندگان: این روش از دانش و تجربیات تصمیم گیرندگان در هر دو مرحله تعیین اوزان معیارها و ارزیابی گزینهها به طور کامل استفاده میکند.
- قابلیت انعطاف پذیری بالا: این روش به راحتی قابل انطباق با مسائل مختلف MCDM با هر تعداد معیار و گزینه است.
- ارائه راهحلهای منطقی و قابل اتکا: این روش با ترکیب دو روش قدرتمند AHP فازی و TOPSIS فازی، راهحلهای منطقی و قابل اتکا برای مسائل MCDM ارائه میدهد.
کاربردهای روش ترکیبی روش TOPSIS-AHP فازی
- انتخاب سبد سرمایهگذاری: انتخاب بهترین سبد سرمایهگذاری با توجه به معیارهایی مانند ریسک، بازده و نقدینگی، با در نظر گرفتن ترجیحات و دیدگاههای سرمایهگذار
- انتخاب محل احداث تأسیسات: انتخاب بهترین مکان برای احداث تأسیسات با توجه به معیارهایی مانند دسترسی به مواد اولیه، نزدیکی به بازار، و هزینه زمین، با در نظر گرفتن الزامات فنی و اقتصادی
- انتخاب بهترین تامین کننده: انتخاب بهترین تامین کننده برای یک محصول یا خدمات خاص با توجه به معیارهایی مانند قیمت، کیفیت، و قابلیت اطمینان، با در نظر گرفتن نیازها و الزامات پروژه
- انتخاب برترین طرح پژوهشی: انتخاب برترین طرح پژوهشی برای اعطای بودجه با توجه به معیارهایی مانند نوآوری، اهمیت، و قابلیت اجرا، با در نظر گرفتن تخصص و دیدگاه داوران
- انتخاب بهترین روش درمانی: انتخاب بهترین روش درمانی برای یک بیماری خاص با توجه به معیارهایی مانند اثربخشی، عوارض جانبی، و هزینه، با در نظر گرفتن شرایط بیمار و نظر پزشک
مثال روش TOPSIS-AHP فازی
این مثال از مقاله A Combination of Fuzzy AHP and TOPSIS Method for the Supplier Selection Problem استخراج شده است. در این مثال شرکت تبلیغاتی مورد نظر، به منظور تامین محصولات چاپی خود، با 5 تامین کننده همکاری می کند که در انتخاب و اولویت بندی این تامین کنندگان، 8 تن از خبرگان این شرکت به عنوان تصمیم گیرنده نقش دارند.
در این پژوهش به منظور ارزیابی و اولویت بندی تامین کنندگان از 8 معیار قیمت محصول، کیفیت، تحویل به موقع، سابقه فعالیت شرکت تامین کننده، گردش مالی، تنوع محصول، خدمات، سیستم ارتباط از راه دوراستفاده شده است.
گام اول: ماتریس یکپارچه مقایسات زوجی معیارها را با کمک میانگین گیری هندسی از میان 8 خبره تشکیل می دهیم.
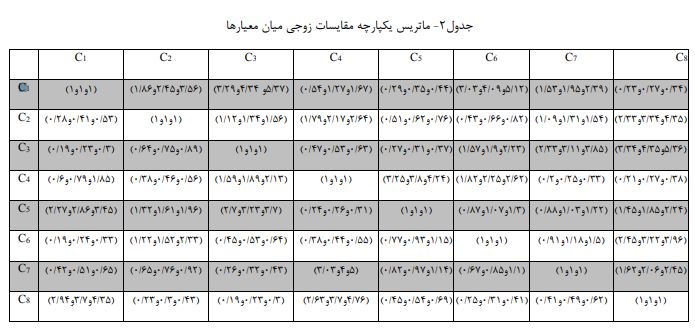
در ادامه مقادیر S از طریق روش AHP فازی محاسبه می گردد.
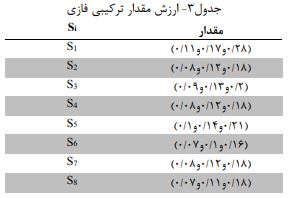
در گام بعدی درجه امکان S را به هم می سنجیم
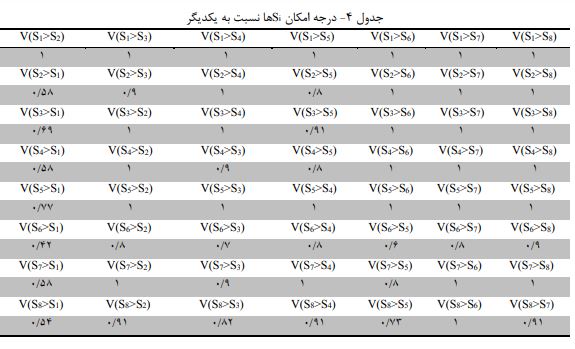
در نهایت اوزان معیارها را بدست می آوریم

با بدست آوردن مقدار اوزان معیارها، زمان آن رسیده که ماتریس گزینه ها را با توجه به این معیارها وزن دار کنیم.
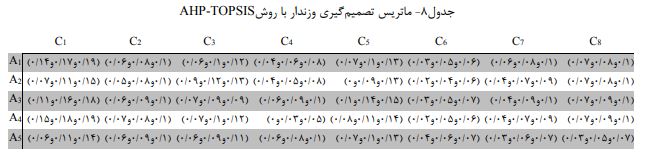
درگام بعدی بر اساس روش TOPSIS فازی جواب ایده آل مثبت و منفی را محاسبه می کنیم.

برای همه گزینه ها فاصله از معیار مثبت و منفی را محاسبه می کنیم.
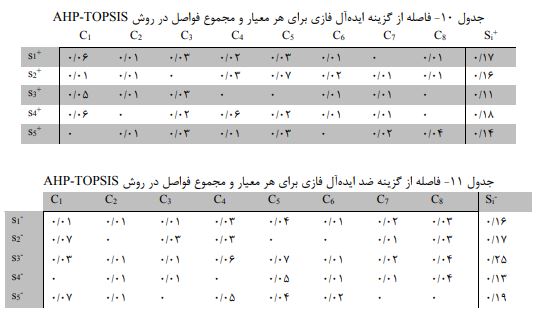
در نهایت شاخص نزدیکی را محاسبه و گزینه ها را رتبه بندی می کنیم.
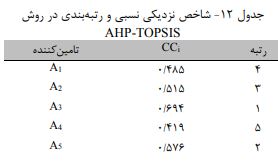
مشاهده می شود که تامین کننده 3 بهترین انتخاب برای ما می باشد.
نتیجهگیری
روش TOPSIS-AHP فازی، رویکردی نوین و کارآمد برای حل مسائل MCDM در شرایطی است که اطلاعات و ترجیحات تصمیم گیرندگان با ابهام و عدم قطعیت همراه باشند. این روش، مزایای هر دو روش AHP فازی و TOPSIS فازی را به طور همزمان به کار میگیرد و ابزاری قدرتمند برای تصمیم گیری در شرایط پیچیده و مبهم فراهم میکند.
با توجه به مزایای روش TOPSIS-AHP فازی، پیشنهاد میشود از این روش در تحقیقات آتی در زمینه MCDM استفاده شود. همچنین، توسعه نرمافزارهایی برای تسهیل پیادهسازی این روش میتواند مفید باشد.
سوالات متداول
روش ترکیبی روش TOPSIS-AHP فازی در مقایسه با روشهای سنتی MCDM چه مزایایی دارد؟
این روش، قابلیت مدلسازی ابهام و عدم قطعیت، استفاده از دانش و تجربیات تصمیم گیرندگان، انعطاف پذیری و ارائه راهحلهای منطقی را دارد که در روشهای سنتی MCDM وجود ندارد.
کاربردهای روش ترکیبی روش TOPSIS-AHP فازی چیست؟
از این روش میتوان در حل مسائل مختلف MCDM مانند انتخاب سبد سرمایهگذاری، انتخاب محل احداث تأسیسات، انتخاب بهترین تامین کننده، انتخاب برترین طرح پژوهشی و انتخاب بهترین روش درمانی استفاده کرد.
چگونه میتوان از روش TOPSIS-AHP فازیدر حل مسائل MCDM استفاده کرد؟
مراحل کلی استفاده از این روش شامل موارد زیر است:
شناسایی معیارها و گزینهها
تعیین اوزان معیارها با استفاده از AHP فازی
ارزیابی گزینهها با استفاده از TOPSIS فازی
رتبهبندی گزینهها و انتخاب بهترین گزینه
