مجموعه های فازی

مجموعه های فازی

مجموعه گردایه‌ای از اشیاء متمایز است. این اشیاء، عضوها یا عناصر مجموعه نامیده می‌شوند. اعضای یک مجموعه ممکن است هر چیزی باشند. مثلاً اعداد، افراد، حروف الفبا، مجموعه‌ای از حقایق مجموعه‌های دیگر و جز اینها، بنابراین منظور از اشیاء در تعریف مجموعه لزوماً اشیاء مادی نیست بلکه هر نهادی را هرچند انتزاعی و کاملاً ذهنی (همچون اعداد) می‌توان در ریاضیات یک شیء دانست و گردایهٔ آن اشیاء را مجموعه‌ای دانست.

معمولاً مجموعه‌ها را با حروف بزرگ لاتین مانند A، B،C نشان می‌دهیم. دو مجموعهٔ A و B برابر هستند اگر اعضای آن یکسان باشند. در ادامه به منظرو تشریح مفهوم مجموعه ها ابتدا انواع مجموعه کلاسیک و فازی مورد بررسی قرار می گیرد.

مجموعه کلاسیک:

در نظریه کلاسیک، یک مجموعه شامل تعدادی از اجزا است که به واسطه خصوصیات مشترک گرد هم جمع شده اند. به عنوان مثال “مجموعه اعداد طبیعی کوچکتر از5″ یا مجموعه ” یک خط در فضای دو بعدی” که به صورت های ذیل می توان آن ها را نشان داد:

•  نمایش عناصر مجموعه

مجموعه اعداد طبیعی کوچکتر از {5, A= {1, 2, 3, 4

• تعریف خصوصیات عناصر مجموعه

یک خط در فضای دو بعدی (R²):  B={(x,y) |ax+by+c =0 , (x,y,a,b,c) € R}

• تابع مشخصه:

 عناصر مجموعه جهانی X را به دومقدار صفر و یک تصویر می کند. عناصری که عضو مجموعه هستند مقدار یک و در غیر این صورت مقدار صفر می گیرند.

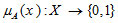
مجموعه های فازی مجموعه های فازی مجموعه های فازی مجموعه های فازی مجموعه های فازی

مجموعه فازی:

اگر X  مجموعه ای از عناصر باشد که با x نشان داده می شود؛ آن گاه مجموعه فازی A³  در X  مجموعه زوج های مرتب به شرح ذیل است:

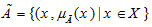
 تابع عضویت یا درجه عضویت x  در مجموعه فوق است. تابع عضویت، مجموعه X را به فضای M  تصویر می کند. اگر فضای تابع عضویت (M) تنها شامل اعداد صفر و یک باشد آنگاه مجموعه مورد نظر، یک مجموعه کلاسیک خواهد بود و اگر M  شامل اعداد حقیقی بین صفر تا یک باشد آنگاه مجموعه مورد نظر، یک مجموعه فازی خواهد بود.

مثال: فرض کنید مجموعه فازی  مجموعه اعداد حقیقی نزدیک به 10 تعریف شود. تابع عضویت آن به شرح ذیل می تواند تعریف شود:

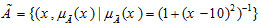
مجموعه های فازی گسسته و پیوسته:

مجموعه گسسته:

اگر عناصر یک مجموعه فازی گسسته باشد به آن مجموعه فازی گسسته گفته می شود که درجه هریک از عناصر آن با یک عدد بین صفر و یک بیان می شود.

تعاریف پایه فازی

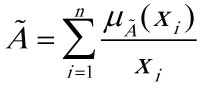
مجموعه پیوسته:

اگر عناصر یک مجموعه فازی پیوسته باشد به آن مجموعه فازی پیوسته گفته می شود که تابع عضویت آن به صورت یک تابع بیان می شود.

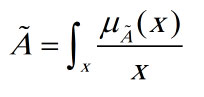
مثال: مجموعه اعداد صحیح مثبت نزدیک به 5 می تواند توسط یک مجموعه فازی گسسته به صورت ذیل تعریف شود:

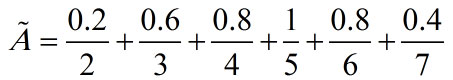
مجموعه اعداد حقیقی غیر منفی نزدیک به 3 نیز توسط یک مجموعه پیوسته با تابع عضویت ذیل قابل تعریف است:

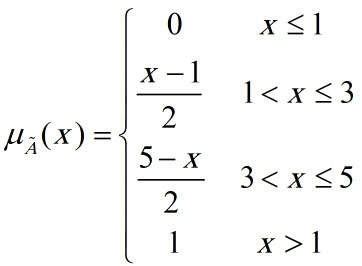
مجموعه پشتیبان:

مجموعه پشتیبان هر مجموعه فازی یک مجموعه کلاسیک است که زیر مجموعه ای از عناصر مجموعه فازی با درجه عضویت مثبت است و به صورت روبرو تعریف می شود.

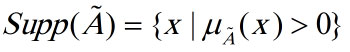
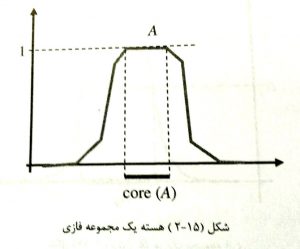
هسته یک مجموعه فازی:

هسته یک مجموعه فازی زیر مجموعه ای از عناصر آن با درجه عضویت یک است.

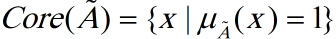
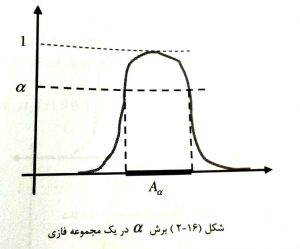
برش  در مجموعه های فازی:

برش  در مجموعه فازی زیر مجموعه ای از عناصر آن است که درجه عضویت آن ها بزرگتر یا مساوی  است و به صورت  نشان داده می شود. اگر برش الفا مساوی نداشته باشد به آن برش قوی گفته می شود.

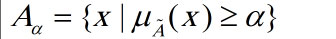
مثال: فرض کنید مجموعه فازی A  روی مجموعه جهانی {X={a,b,c,d,e,f  به صورت ذیل تعریف می شود:

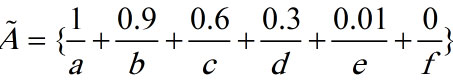
مجموعه فازی محدب:

مجموعه فازی  محدب است اگر داشته باشیم:

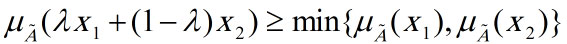
عددی بین صفر و یک است.

ارتفاع مجموعه فازی:

ارتفاع یک مجموعه فازی برایر حداکثر درجه عضویت عناصر آن مجموعه است.

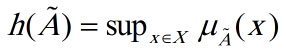
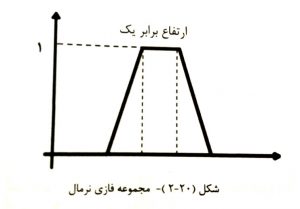
مجموعه فازی نرمال:

مجموعه فازی A  نرمال است اگر ارتفاع آن برابر یک باشد در غیر این صورت مجموعه زیر نرمال است.

در ادامه بخوانید

• نظریه مجموعه های فازی
• مجموعه های فازی
• عملیات در مجموعه های فازی
• اعداد فازی

تصمیم گیری چند معیاره

تصمیم‌گیری شامل بیان درست اهداف، تعیین راه‌حل‌های مختلف و ممکن، ارزیابی امکان‌پذیری آنان، ارزیابی عواقب و نتایج ناشی از اجرای هر یک از راه‌حل‌ها و بالاخره انتخاب و اجرای آن می‌باشد. کیفیت مدیریت اساساً تابع کیفیت تصمیم‌گیری است زیرا کیفیت طرح و برنامه‌ها، اثربخشی و کارآمدی راهبردها و کیفیت نتایجی که از اعمال آن‌ها بدست می‌آید همگی تابع کیفیت تصمیماتی است که مدیر اتخاذ می‌نماید.

در اکثر موارد تصمیم‌گیری‌ها وقتی مطلوب و مورد رضایت تصمیم‌گیرنده است که تصمیم‌گیری براساس چندین معیار مورد بررسی قرار گرفته باشد. معیارها ممکن است کمی یا کیفی باشند. در روش‌های تصمیم‌گیری چند معیاره که در دهه‌های اخیر مورد توجه محققین قرار گرفته‌است به جای استفاده از یک معیار سنجش بهینگی از چند معیار سنجش استفاده می‌شود.

خدمات فرابگیر

1. تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
2. مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
3. برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
4. طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
5. خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
6. پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تص
7. آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت

باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.