در بسیاری از مسائل علمی و مهندسی، یافتن نقطه بهینه یک تابع، چالشی مهم محسوب می شود. این نقطه، بهترین مقدار تابع را در فضای جستجو نشان می دهد. روش
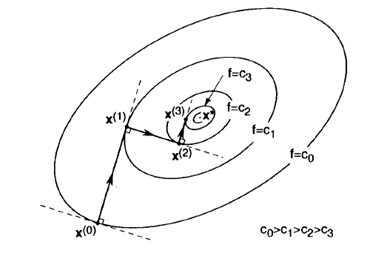
روش تندترین شیب یک الگوریتم ساده، کارآمد و انعطافپذیر برای حل مسائل بهینهسازی محدب است و حل مثال روش تندترین شیب می تواند دیدگاه خوبی را به شما در مورد
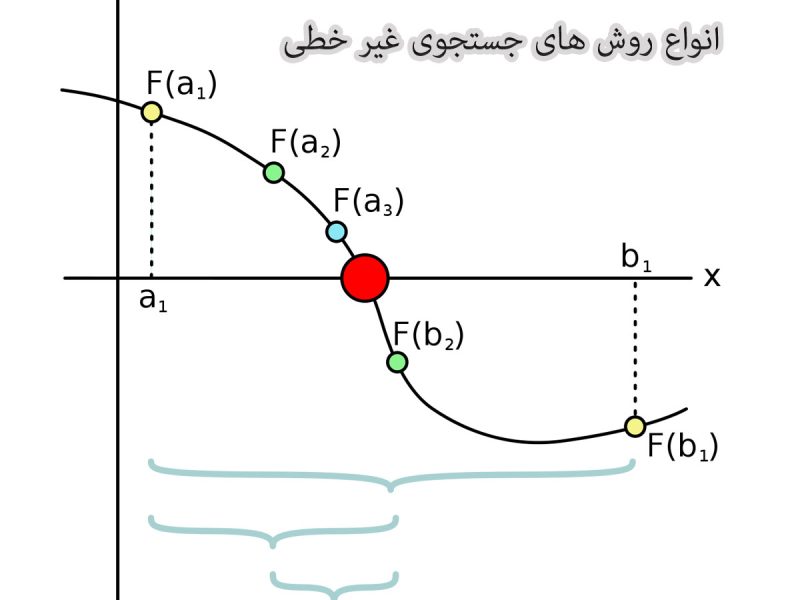
تصور کنید در یک چشمانداز پهناور و مه آلود ایستادهاید، جایی که هدف شما رسیدن به عمیقترین نقطه دره است، اما دیدتان تنها به چند متر مربع اطراف محدود میشود.
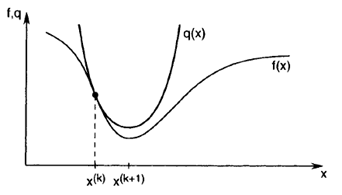
قبل از حل مثال روش نیوتن رافسون باید بدانیم که روش نیوتن-رافسون یک روش قدرتمند برای یافتن ریشههای توابع پیوسته و مشتقپذیر است. این روش مزایای متعددی مانند سرعت بالا،
روش نیوتن-رافسون (Newton-Raphson Method) یک الگوریتم عددی قدرتمند برای یافتن ریشه معادلات غیرخطی تک متغیره است. این روش از تقریب خطی برای تخمین ریشه معادله در هر مرحله استفاده میکند.
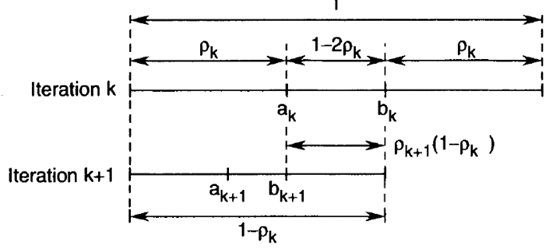
قبل از تشریح مثال روش جستجوی فیبوناچی بهتر است با کلیات این روش آشنا شویم. در سال 1962، دو ریاضیدان به نامهای Kiefer و Wolfowitz روش جستجوی فیبوناچی را برای
روش جستجوی فیبوناچی (Fibonacci Search Method) یک الگوریتم عددی قدرتمند برای یافتن ریشه معادلات غیرخطی تک متغیره است. این روش از دنباله اعداد فیبوناچی، که در طبیعت و ریاضیات نقشی
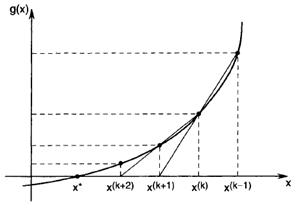
برای مثال روش سکانت جهت یافتن ریشه معادله g(x) = x3 – 12.2×2 +7.45x +42 =0 استفاده نمایید. نقاط اولیه برای شروع را به ترتیب x(-1) = 13 و x(0)
روش سکانت (Secant Method) که به نام روش خطوط نیز شناخته میشود، یک روش عددی برای یافتن ریشه معادلات غیرخطی تک متغیره است. این روش از دو نقطه دلخواه روی
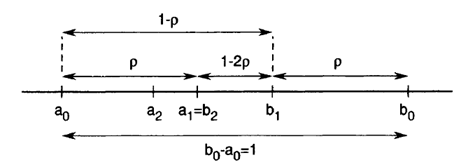
در ادامه مثال روش جستجوی طلایی را تشریح می نماییم. می خواهیم با استفاده از روش جستجوی طلایی نقطه x را طوری تعیین نماییم که تابع هدف f(x) = x4-14×3+60×2-70x