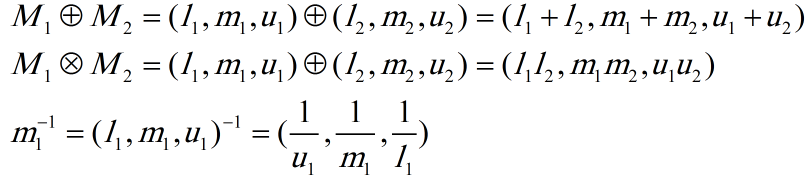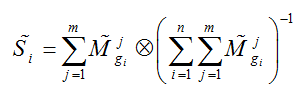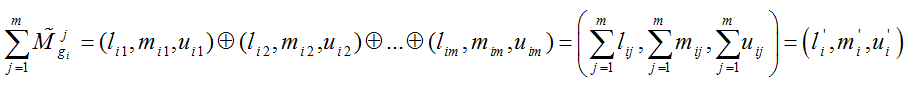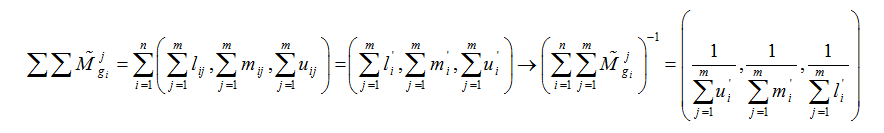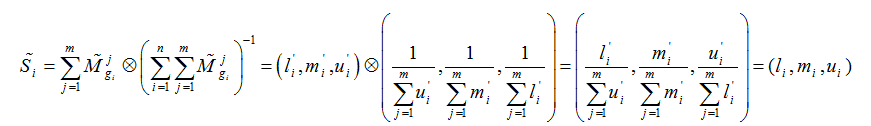ای اچ پی فازی
پس از معرفی روش AHP فازی توسط ساعتی، به دلیل اهمیت بسیار زیاد استفاده از مفاهیم فازی در تصمیم گیری ها، در سال های اخیر این روش توسط پژوهشگران بسیاری توسعه داده شده است که در این میان می توان به روش های ارائه شده توسط بالکی، لارهون و پدریک، کولاک و کاهرمان و غیره اشاره نمود. روشی که در این بخش توضیح داده خواهد شد در سال 1996 توسط یک پژوهشگر چینی به نام چانگ ارائه شده است.
AHP فازی
در این روش با استفاده از عبارت های زبانی موجود در جدول زیر، مفهوم فازی بودن در تعیین ماتریس های مقایسه زوجی دخالت داده می شود. بنابراین با تعمیم موارد فوق، روش های ارائه می گردد که در آن ها از اعداد فازی برای بیان میزان ارجحیت المان ها استفاده می شود.
ای اچ پی فازی
مقادیر عددی ارجحیت ها در مقایسات زوجی
| عبارت زبانی برای تعیین ارجحیت | مقدار عددی |
| ارجحیت با اهمیت کامل و مطلق | 9 |
| ارجحیت با اهمیت خیلی قوی | 7 |
| ارجحیت با اهمیت قوی | 5 |
| ارجحیت با اهمیت کم | 3 |
| ارجحیت با اهمیت برابر | 1 |
| برای ترجیحات بین عبارت های زبانی فوق | 2و4و6و8 |
برای توضیح روش AHP فازی در ابتدا به تشریح روش آنالیز توسعه ی چانگ پرداخته می شود، زیرا این روش از سایر روش های AHP فازی ساده تر بوده و در ضمن مشابه با روش AHP کلاسیک است. مفاهیم مورد استفاده درAHP فازی به روش آنالیزتوسعه عبارتند از:
تعریف 1: در این روش برای پیشگیری از ابهام ناشی از عدم قطعیت در تصمیم گیری در همه مراحل اعداد فازی مثلثی به کاربرده شده است. یک عدد فازی مثلثی که با (m=(I, m, u نشان داده می شود.
بیشتر بدانیم
تعریف 2: اگر دو عدد فازی مثلثی مثل (M1=(l1, m1, u1 و (M2=(l2, m2, u2 وجود داشته باشد، به طوری که l1,m1,u1>0 آن گاه:
ای اچ پی فازی
چنان چه {X={x1, x2, … , xn مجموعه اهداف و {U={u1, u2, … , un مجموعه آرمان ها معرفی شوند، آنگاه بر طبق روش آنالیز توسعه ی چانگ با در نظر گرفتن هر هدف، آنالیز توسعه را می توان برای هر یک از آرمان ها (gi) انجام داد؛ بنابراین می توان به صورت زیر m مقدار آنالیز توسعه برای هر هدف داشت:
حال می توان مراحل آنالیز توسعه چانگ را به صورت زیر بیان نمود:
مرحله1: در مرحله اول باید بسط مرکب فازی را برای هر هدف به دست آورد. اگر M1gi, M2gi,…, Mngi مقادیر آنالیز توسعه iامین هدف به ازای m آرمان باشد آنگاه مقدار بسط مرکب فازی برای iامین معیار به صورت زیر تعریف می گردد:
که در این فرمول j، نماینده هرکدام از آرمان ها می باشد. چنان چه (M1gi = (lij, mij, uij باشد آنگاه Mjgi ∑ بوسیله عملگر جمع فازی روی آنالیز توسعه m آرمان به صورت زیر تعریف می گردد:
همچنین برای به دست آوردن Mjgi]-1∑∑ ] با اعمال عملگر جمع فازی خواهیم داشت:
بنابراین:
مرحله2: محاسبه درجه ارجحیت ( درجه ی امکان پذیری) Si برSk.
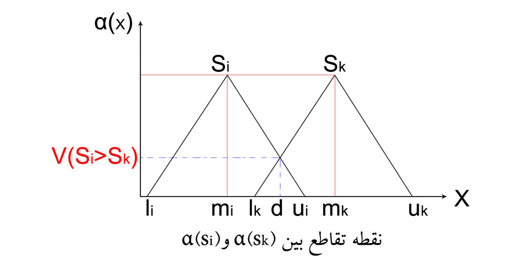
چنانچه (Si=(li, mi, ui و (Sk=(lk, mk, uk باشد، آنگاه درجه ی ارجحیت Si بر Sk که با (V(Si>Sk نمایش داده می شود، به صورت زیر تعریف می گردد:
V(Si>Sk) = SUPx≥y (min {αsi(x), αsk(y)})
که برای اعداد فازی مثلثی معادل با رابطه ی زیر است:
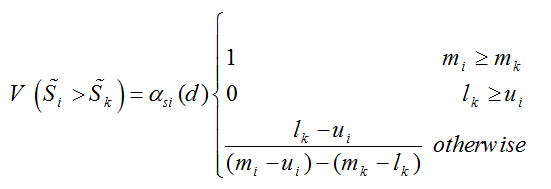
که d متناظر با بزرگ ترین نقطه ی تقاطع بین skα و siα است. شکل زیر مقدار (V(Si>Sk را نشان می دهد.
مرحله 3: محاسبه درجه اهمیت درجه امکان پذیری یک عدد فازی محدب S که بزرگ تر از k عدد فازی محدب Si: i=1,2,…,k باشد به صورت زیر تعریف می گردد:
V (S≥S1,S2,…,Sk) = V((S≥S1), (S≥S2),…,(S≥Sk))=min{(V(S≥S1), V(S≥S2),…,V(S≥Sk)}=min{ (S≥Si)} i=1,2,..,k
چنان چه فرض کنیم که k=1,2,…,n باشد و (d'(Ai)=min V(Si≥Sk باشد آنگاه بردار وزن به صورت زیر بدست می آید:
W’ = (d'(A1), d'(A2)… d'(An))
قابل ذکر است که وزن های بدست آمده غیر فازی هستند.
مرحله4: نرمالیزه کردن بردار W’ و بدست آوردن بردار وزن نرمالیزه شده.
W = (d(A1), d(A2)… d(An))