قبل از اینکه در مورد برنامه ریزی آرمانی فازی توضیح دهیم لازم است ابتدا با برنامه ریزی آرمانی آشنا شویم. مدل های برنامه ریزی آرمانی در ابتدا توسط Charnes و Cooper در اوایل سال 1961 برای یک مدل خطی معرفی شدند. این رویکرد امکان حل همزمان سیستمی از اهداف پیچیده را فراهم می کند و حل مشکل مستلزم ایجاد رابطه بین اهداف متعدد است.
مفهوم اصلی برنامه ریزی آرمانی خطی این است که اهداف اصلی چندگانه را به هدف عددی خاص برای هر هدف تبدیل کند. سپس تابع هدف فرموله می شود و راه حلی جستجو می شود که مجموع وزنی انحرافات از هدف مربوطه را به حداقل برساند.
آنچه می خوانید
در این مقاله ابتدا با مفهوم برنامه ریزی آرمانی فازی آشنا می شویم. در ادامه با ارائه یک مثال این مفهوم کلیدی در برنامه ریزی خطی را شرح می دهیم.
برنامه ریزی آرمانی فازی
به طور کلی، مدل های برنامه ریزی آرمانی از سه جزء تشکیل شده است:
یک تابع هدف، مجموعه ای از محدودیت های هدف، و الزامات غیر منفی. با این حال، مقدار هدف مرتبط با هر هدف می تواند در برنامه دنیای واقعی مبهم باشد.
تئوری مجموعه های فازی به طور مکرر در تحقیقات اخیر استفاده می شود. یک مجموعه فازی A را می توان با یک تابع عضویت مشخص کرد، که معمولا با علامت μ مشخص می شود، که به هر شی از یک دامنه درجه عضویت خود را در A اختصاص می دهد.هر چه بیشتر بتوان گفت یک عنصر یا شی به مجموعه فازی A تعلق دارد، درجه عضویت آن به 1 نزدیکتر است.
انواع مختلفی از توابع عضویت را می توان برای پشتیبانی از چارچوب تحلیلی فازی استفاده کرد، اگرچه توصیف فازی فرضی است و مقادیر عضویت ذهنی هستند. توابع عضویت مانند توابع خطی، خطی تکه ای، نمایی و هذلولی در تحلیل های مختلف مورد استفاده قرار گرفتند. به طور کلی، توابع عضویت خطی غیرافزاینده و غیر کاهشی اغلب برای نابرابریهای با روابط کمتر یا مساوی و بزرگتر یا مساوی استفاده میشوند.
از آنجایی که روش حل برنامه ریزی آرمانی فازی برآورده کردن هدف فازی است، بنابراین تصمیم در یک محیط فازی به عنوان تقاطع آن توابع عضویت مربوط به اهداف فازی تعریف می شود. از این رو، تصمیم بهینه می تواند هر جایگزینی در چنین فضای تصمیم گیری باشد که می تواند حداقل را به حداکثر برساند، که توسط آن توابع عضویت مربوطه نمایش داده می شود.
تفاوت بین برنامه ریزی آرمانی فازی و برنامه ریزی خطی سنتی
برنامه ریزی خطی سنتی فرض می کند که همه اهداف و محدودیت ها به طور قطعی شناخته شده اند. با این حال، در برنامه ریزی آرمانی فازی، اهداف و محدودیت ها می توانند به صورت فازی بیان شوند، به این معنی که دقیقاً مشخص نیستند و محدوده ای از مقادیر ممکن را دارند.
مزایای استفاده از برنامه ریزی آرمانی فازی
برنامه ریزی آرمانی فازی مزایای متعددی دارد، از جمله:
- می تواند برای حل مسائلی که با عدم قطعیت و ابهام همراه هستند استفاده شود.
- می تواند اهداف و ترجیحات تصمیم گیرندگان مختلف را به طور همزمان در نظر بگیرد.
- می تواند راه حل های انعطاف پذیرتر و واقع بینانه تری ارائه دهد.
مراحل برنامه ریزی آرمانی فازی
مراحل برنامه ریزی آرمانی فازی به شرح زیر است:
- تعریف اهداف و محدودیت ها: اهداف و محدودیت های مسئله را به صورت فازی تعریف کنید.
- مدل سازی ریاضی: یک مدل ریاضی برای مسئله بر اساس برنامه ریزی آرمانی فازی ایجاد کنید.
- حل مدل: مدل ریاضی را با استفاده از روش های مناسب حل کنید.
- تجزیه و تحلیل نتایج: نتایج را تجزیه و تحلیل کرده و راه حل های مناسب را انتخاب کنید.
مساله برنامه ریزی آرمانی
مسئله برنامه ریزی آرمانی برنامه ریزی هدف یک مدل برنامه ریزی ریاضی چندهدفه است که تلاش می کند یک راه حل بهینه برای چندین هدف متضاد ایجاد کند. راه حل بهینه، رضایت بخش ترین راه حل در مجموعه ای از راه حل های امکان پذیر خواهد بود.
مدل برنامه ریزی آرمانی یک تکنیک انعطافپذیرتر است که درک و استفاده از آن نسبتاً آسان است. کاربردهای قبلی برنامه ریزی آرمانی در تنظیمات صنعتی و تولیدی وجود داشته است، اما هیچ یک از استفاده های اولیه GP به صراحت ترجیحات تصمیم گیرنده را در بر نمی گیرد. هدف کلی GP به حداقل رساندن انحرافات بین دستیابی به اهداف و سطوح آرمان آنها است.
یک برنامه ریزی آرمانی معمولی به صورت زیر بیان می شود:
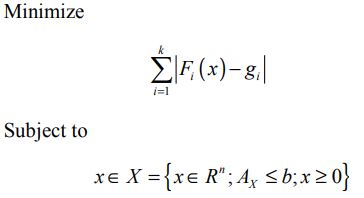
جایی که Fi برنامه ریزی خطی تابع هدف i و gi سطح آرمان هدف است. در نظر بگیرید:
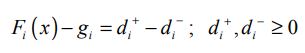
معادله (1) را می توان به صورت زیر فرموله کرد:
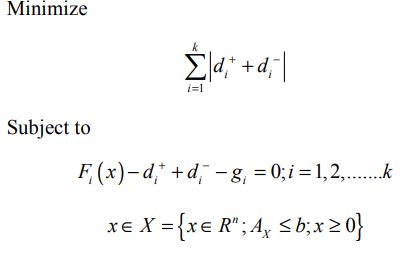
به طوری که di+>=0 و di->=0 انحراف از هدف اول می باشند.
مساله برنامه ریزی آرمانی فازی
نراسیمهان و همکاران اولین کسانی بودند که با استفاده از مفهوم توابع عضویت، فرمول برنامه ریزی آرمانی فازی (FGP) را ارائه کردند. این توابع در بازه [0، 1] تعریف می شوند. بنابراین، تابع عضویت برای هدف i-امین زمانی که این هدف محقق شود و چند معیار تصمیم کاملاً برآورده شود، مقدار 1 دارد. در غیر این صورت برای تابع عضویت مقداری بین 0 و 1 در نظر می گیرد.
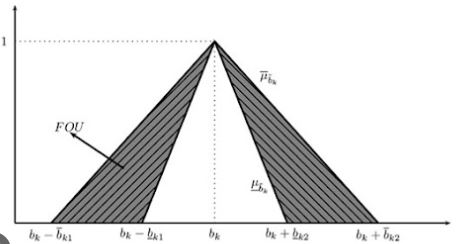
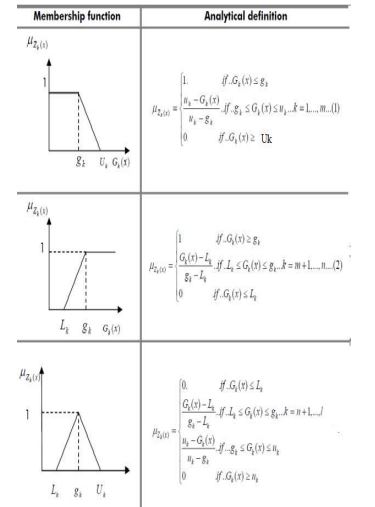
توابع عضویت خطی در ادبیات و عمل بیشتر از انواع دیگر توابع عضویت استفاده می شود. برای سه نوع هدف فازی بالا، توابع عضویت خطی به صورت زیر تعریف و نشان داده می شوند (شکل 1): جایی که Lk (یا uk ) حد تحمل پایین تر برای هدف فازی k.ام است. آنها یا به صورت ذهنی با تصمیم گیرنده و یا با تلورانس ها در یک فرآیند فنی انتخاب می شوند.
اصطلاحات زبانی فازی برای تعیین درجه مطلوبیت
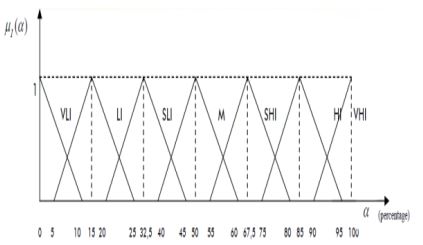
تعیین درجه مطلوبیت برای یک هدف می تواند برای تصمیم گیری در یک محیط فازی هنگام استفاده از این روش کار دشواری باشد. برای ارزیابی دقیق درجات موفقیت مطلوب، یک روش مفید استفاده از اصطلاحات زبانی مانند “کم اهمیت”، “تا حدودی بسیار مهم” و “بسیار بالا مهم” و غیره برای توصیف شفاهی اهمیت هر هدف فازی است. سپس توابع عضویت مرتبط تعریف می شوند.
ما می توانیم ( ) I u α را برای نشان دادن تابع عضویت هر یک از مقادیر زبانی در مورد اهمیت اهداف مختلف تعریف کنیم، که در آن uI (α) بین صفر و یک و α نشان دهنده متغیری است که درجه موفقیت را در بازه [α min , α max] به صورت 0 کوچکتر از α min و کوچکتر از α max و کوچکتر از 1 تعیین می کند.
روشهای رتبهبندی اعداد فازی میتوان برای ترسیم تابع عضویت که نشاندهنده اهمیت یک هدف فازی به یک عدد واقعی در محدوده [۰،۱] است استفاده کرد. عدد واقعی به دست آمده را می توان به عنوان درجه موفقیت مطلوب برای هدف فازی در نظر گرفت. ما مجموعه زیر را تعریف می کنیم:
| اعداد فازی مثلثی | مقادیر زبانی |
|---|---|
| (0,0, 10%) | VLI = Very Low Important |
| (5%,15%, 25%) | LI = Low Important |
| (20%,32/5%, 45%) | SLI = Somewhat Low Important |
| (40%، 50%، 60%) | M = Medium |
| (55%، 67.5%، 80%) | SHI = Somewhat High Important |
| (75%، 85%، 95%) | HI = High Important |
| (90%, 100%, 100%) | VHI =Very High Important |
مثال برنامه ریزی آرمانی فازی
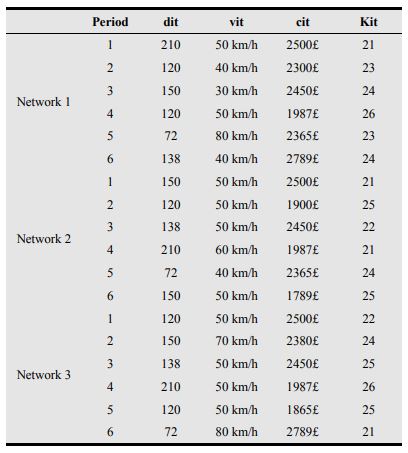
در این بخش به مورد یک شرکت حمل و نقل مشترک می پردازیم که با به حداقل رساندن تعداد تصادفات جاده ای برای هر وسیله نقلیه (اتوبوس) به دنبال به حداکثر رساندن سودآوری خدمات مشتریان خود است. یک اتوبوس در سه شبکه اصلی فعالیت می کند: 1: دانشگاه، 2: مرکز شهر و 3: منطقه صنعتی.
این جابه جایی ها بر مبنای پارامترها و مقادیر ثابت های زیر انجام می شود:
- dit : زمان سفر راننده i برای دوره j
- cit: اطمینان از هزینه تصادف راننده i در دوره j
- rt: هزینه نیروی کار به ازای هر ساعت کارمند در دوره t.
- vit : سرعت متحمل شده توسط راننده i در دوره j
- Kit: سطح دانش راننده شبکه جاده i در دوره t
- Iio: تعداد تصادفات ایجاد شده توسط رانندگان i در دوره t -1
- T: برنامه ریزی مسیرهای افق سفر
- N: تعداد کل رانندگان
- Pit: تعداد مسئول بلیط i در دوره t
- Iit: تعداد تصادفات انجام شده توسط رانندگان i در دوره t
- Ht: کارگر استخدام شده در دوره t
- Ft: کارگران اخراج شده در دوره t
- IIT min: حداقل مسئول بلیط i در دوره t
- Wt: تعداد کل اتوبوس ها در طول دوره t
- WMin: حداقل تعداد اتوبوس های موجود در دوره t
- WMax: حداکثر تعداد اتوبوس های موجود در دوره t
پیاده سازی مدل پیشنهادی در شرکت دارای شرایط زیر است:
- شش دوره افق برنامه ریزی وجود دارد
- سه شبکه جاده ای
- تعداد حداقل تصادفات ایجاد شده توسط رانندگان i در دوره t -1: I10 = 18 تصادف در شبکه 1، I20 = 10 تصادف در شبکه 2، I30 = 33 تصادف در شبکه 3
- حداقل تعداد تصادف در دوره t رانندگان i 30 تصادف غیر فوتی است
- هزینه تعمیر یا خرید مجدد تصادف اتوبوس در هر اتوبوس به ترتیب 10386 پوند و 27900 پوند است.
- ارزش های زبانی در مورد اهمیت اهداف به ترتیب عبارتند از: بسیار بالا مهم = VHI، بسیار مهم = HI، متوسط = M.. و با فرض اینکه تصمیم گیرنده متوسطی داریم، با α = 0.5.
- هزینه یک راننده در اتوبوس شبکه سه در طول دوره t برابر با 2500 پوند / نفر است.
- حداقل تعداد اتوبوس های موجود در دوره t برابر WMin = 50 اتوبوس در سه شبکه است
- حداقل تعداد اتوبوس های موجود در دوره t برابر WMax = 80 اتوبوس در سه شبکه است.
- تعداد اولیه اتوبوس WMin = 130 اتوبوس شبکه سه.
- حداکثر تعداد تصادفات ایجاد شده توسط رانندگان i در دوره t سه شبکه 80 تصادف می باشد.
فرمول بندی و حل مساله برنامه ریزی آرمانی فازی
ابتدا توابع عضویت را می سازیم. تابع عضویت خطی هر تابع هدف با درخواست از تصمیم گیرندگان برای تعیین بازه [kg…k u] مقادیر هدف، و همچنین تعیین معادل بودن این مقادیر هدف به عنوان مقدار عضویت در فاصله [0، 1] تابع تعیین می شود. تابع عضویت خطی و پیوسته برای کمی کردن سطوح آرمانی فازی مناسب است.
تابع 1: به حداقل رساندن کل هزینه تضمین تصادف
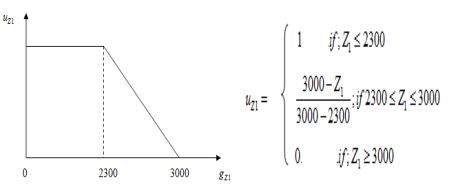
عملکرد 2: به حداقل رساندن سرعت کل
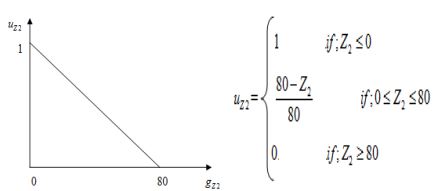
عملکرد 3: به حداقل رساندن تغییرات در زمان کار
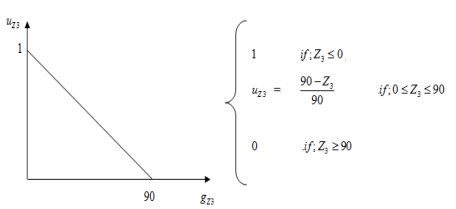
سپس، توابع هدف عبارتند از:
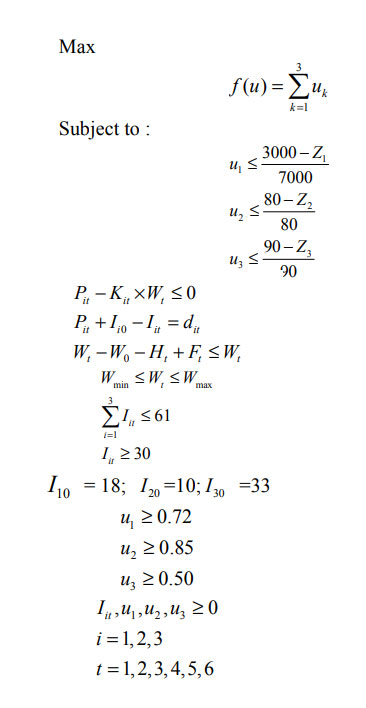
از نرم افزار LINGO برای اجرای مدل برنامه نویسی استفاده می شود.
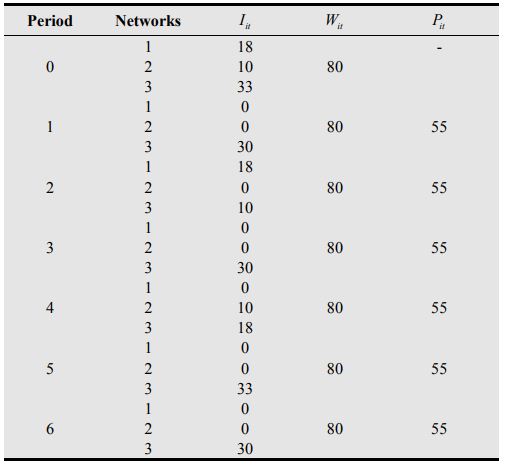
استفاده از برنامهریزی آرمانی فازی برای به حداقل رساندن همزمان هزینههای کل تصادفات جادهای (Z1)، هزینههای حمل (Z2)، و تغییرات در سطوح نیروی کار (Z3)، هزینه کل تصادفات جادهای 2999 پوند را به همراه دارد و درجات دستیابی به سه هدف فازی را به همراه دارد. مقادیر u1,u2,u3 به ترتیب 0، 0 و 1 هستند که همگی الزامات تصمیم گیرندگان را برآورده می کنند.
تصمیم گیری چند معیاره
تصمیمگیری شامل بیان درست اهداف، تعیین راهحلهای مختلف و ممکن، ارزیابی امکانپذیری آنان، ارزیابی عواقب و نتایج ناشی از اجرای هر یک از راهحلها و بالاخره انتخاب و اجرای آن میباشد. کیفیت مدیریت اساساً تابع کیفیت تصمیمگیری است زیرا کیفیت طرح و برنامهها، اثربخشی و کارآمدی راهبردها و کیفیت نتایجی که از اعمال آنها بدست میآید همگی تابع کیفیت تصمیماتی است که مدیر اتخاذ مینماید.
در اکثر موارد تصمیمگیریها وقتی مطلوب و مورد رضایت تصمیمگیرنده است که تصمیمگیری براساس چندین معیار مورد بررسی قرار گرفته باشد. معیارها ممکن است کمی یا کیفی باشند. در روشهای تصمیمگیری چند معیاره که در دهههای اخیر مورد توجه محققین قرار گرفتهاست به جای استفاده از یک معیار سنجش بهینگی از چند معیار سنجش استفاده میشود.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چندمعیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.
