تاپسیس فازی
مزیت این روش بر روش کلاسیک آن بکارگیری متغیرهای زبانی که بوسیله اعداد فازی ارائه شده اند می باشد که در نتیجه برای تغییر وزن ها در رتبه بندی گزینه ها استفاده از مقادیر دقیق و معین لازم نیست. چن(chen) و هوانگ راه حل روش شباهت به گزینه ایده ال فازی را به صورت زیر ارائه کرده اند:
مرحله اول: تشکیل ماتریس تصمیم
با توجه به معیارها و گزینه ها ماتریس تصمیم به صورت زیر تشکیل می شود که در آن xij عملکرد گزینه i نسبت به معیار j است.
در صورت استفاده از اعداد فازی مثلثی: xij = (aij, bij, cij)
در صورت استفاده از اعداد فازی ذوزنقه ای: xij = (aij, bij, cij, dij)
اگرکمیته تصمیم گیرنده k عضو داشته باشد و عدد فازی مثلثی:
xij = (aij, bij, cij)
aij = Min { aij k} , bij = ∑bijk /k , cij = Max { cij k}
اگر کمیته تصمیم گیرنده k عضو داشته باشد و عدد فازی ذوزنقه ای:
xij = (aij, bij, cij, dij)
aij = Min { aij k} , bij = ∑bijk /k , cij = ∑cijk /k , dij = Max { dij k}
تاپسیس فازی تاپسیس فازی تاپسیس فازی تاپسیس فازی تاپسیس فازی
مرحله دوم: بی مقیاس کردن ماتریس تصمیم فازی:
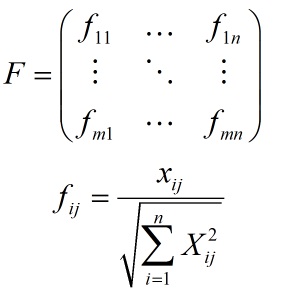
در این روش برای بی مقیاس کردن از تغییر مقیاس خطی (Linear Scale Transformating) استفاده می شود که در آن اگر اعداد فازی به صورت مثلثی باشند درایه های ماتریس تصمیم بی مقیاس شده و به صورت زیر محاسبه می شوند:
برای اعداد فازی مثلثی
rij = (aij / c*j, bij / c*j, cij / c*j) معیار های مثبت -> c*j = Max Cij ماکسیمم مولفه های سوم در هر ستون اعداد مثلثی
rij = (a–j / cij, a–j / bij, a–j / aij) معیار های منفی -> a–j = Min aij مینیمم مولفه های اول در هر ستون اعداد مثلثی
برای اعداد فازی ذوزنقه ای
rij = (aij / d*j, bij / d*j, cij / d*j, dij / d*j) معیار های مثبت -> d*j = Max dij ماکسیمم مولفه های چهارم در هر ستون اعداد ذوزنقه
rij = (a–j / dij, a–j / cij, a–j / bij, a–j / aij) معیار های منفی -> a–j = Min aij مینیمم مولفه های اول در هر ستون اعداد ذوزنقه
ماتریس تصمیم فازی بی مقیاس شده R به صورت زیر می باشد:
R= [rij] i=1…n , j=1…m
مرحله سوم: تعیین ماتریس وزن معیارها: که در این مرحله ضریب اهمیت معیارهای مختلف به صورت زیر تعریف می شود ( صورت مساله یا از طریق DM به ما داده می شود:
اعداد فازی مثلثیw=[wj1,wj2,wj3 ,wj4] اعداد فازی ذوزنقه ای w=[wj1,wj2,wj3]
تاپسیس فازی
اگر کمیته تصمیم گیرنده دارای k عضو باشد آنگاه داریم:
اعداد مثلثی
wj1 = Min {wj1k}
wj2 = ∑ wj2k/k
wj3 = Max {wj3k}
تاپسیس فازی تاپسیس فازی تاپسیس فازی تاپسیس فازی تاپسیس فازی
اعداد ذورنقه ای
wj1 = Min {wj1k}
wj2 = ∑ wj2k/k
wj3 = ∑ wj3k/k
wj4 = Max {wj4k}
تاپسیس فازی
مرحله چهارم: تعیین ماتریس تصمیم فازی وزن دار:
این ماتریس از ضرب کردن ضریب اهمیت مربوط به هر معیار در ماتریس بی مقیاس شده فازی به صورت زیر بدست می آید:
V = [Vij] i=1…n, j=1…m -> Vij = rij * wij
اعداد مثلثی
برای معیارها با جنبه مثبت Vij = rij * wij -> (wj1 * (aij / c*j) , wj2 * (bij / c*j) , wj3 * (cij / c*j))
برای معیارها با جنبه منفی Vij = rij * wij -> (wj1 * (a–j / cij) , wj2 * (a–j / bij) , wj3 * (a–j / aij))
اعداد ذوزنقه ای
برای معیارها با جنبه مثبت Vij = rij * wij -> (wj1 * (aij / d*j) , wj2 * (bij / d*j) , wj3 * (cij / d*j) , wj4 * (dij / d*j))
برای معیارها با جنبه منفی Vij = rij * wij -> (wj1 * (a–j / dij) , wj2 * (a–j / cij) , wj3 * (a–j / bij) , wj4 * (a–j / aij))
تاپسیس فازی
مرحله پنجم: یافتن حل ایده آل فازی و حل ضد ایده آل فازی:
ایده آل A* = {V*1, V*2… V*n}
ایده آل ضد A– = {V–1, V–2… V–n}
در اینجا مقادیر V*i و V–i خود اعداد فازی مثلثی یا ذورنقه ای می باشند که هر یک از مولفه های آن ها از روابط بالا بدست می آید. در واقع این اعداد، 3 تایی یا 4 تایی هایی اند که تمام مولفه های آن ها با هم برابر و برابر مقدار Max{Vij3} و Min{ Vij1} می باشند.
تاپسیس فازی تاپسیس فازی تاپسیس فازی تاپسیس فازی تاپسیس فازی
V*i بهترین مقدار معیار از بین گزینه ها (ماکسیمم مولفه سوم در ستون مربوطه) = Max {Vij3}
V–i بدترین مقدار معیار از بین گزینه ها (مینیمم مولفه اول در ستون مربوطه) = Min {Vij1}
اعداد ذوزنقه ای
V*i بهترین مقدار معیار از بین گزینه ها (ماکسیسمم مولفه چهارم در ستون مربوطه) =Max {Vij4}
V–i بدترین مقدار معیار از بین گزینه ها (مینیمم مولفه اول در ستون مربوطه) = Min {Vij1}
تاپسیس فازی
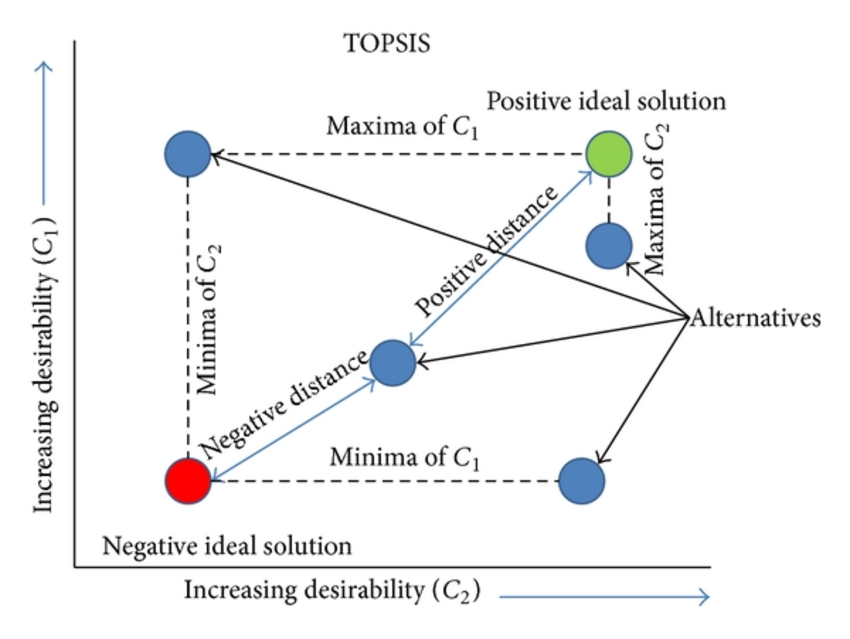
مرحله ششم: محاسبه فاصله از حد ایده آل و ضد ایده آل فازی:
فاصله هر گزینه از حد ایده آل و ضد ایده به ترتیب از روابط زیر بدست می آید:
ایده ال S*i =∑ d (Vij, V*ij) ضد ایده ال S–i =∑ d (Vij, V–ij)
ابتدا فاصله هر گزینه با گزینه ایده آل هر معیار به صورت تک تک محاسبه می شود. سپس مجموع این فواصل در نظر گرفته می شوند. یعنی اگر یکی از گزینه ها را نسبت به گزینه S*i بخواهیم، باید فاصله آن را از S*11 و S*12وS*13 محاسبه شده و سپس Sij)∑( آن در نظر گرفته می شود.
حالت مثلثی: اگر عدد فازی اول M1=(a1,b1,c1) و عدد فازی دوم M2=(a2,b2,c2) نشان دهیم فاصله آن ها به صورت:
D (M1, M2) = ∑ 1/3[(a1-a2)2 + (b1-b2)2 + (c1-c2)2]
حالت ذوزنقه ای: اگر عدد فازی اول (M1=(a1,b1,c1,d1 و عدد فازی دوم (M2=(a2,b2,c2,d2 نشان دهیم فاصله آن ها به صورت:
D (M1, M2) = ∑ 1/4[(a1-a2)2 + (b1-b2)2 + (c1-c2)2+ (d1-d2)2]
فواصل D اعدادی قطعی می باشند.
تاپسیس فازی
مرحله 7: محاسبه شاخص شباهت:
Ci = Si– / (Si* + Si–) i=1…n
مرحله 8 : رتبه بندی گزینه ها: با توجه به شاخص شباهت صورت می گیرد.
خدمات فرابگیر
- تبلیغات در فضای مجازی گوگل، اینستاگرام و فیس بوک.
- مدیریت صفحات اجتماعی اینستاگرام و فیس بوک.
- برنامه نویسی حرفه ای با جدیدترین متدهای روز دنیا
- طراحی وب سایت و سئو نمودن مطالب با جدیدترین راهکارها برای بازدید حداکثری مطالب
- خدمات طراحی سربرگ؛ کار ویزیت، لوگو و بسته مدیریتی
- پروژهای دانشجویی در زمینه تحقیق در عملیات، آمار و تصمیم گیری چند معیاره
- آموزش مجازی برای کاربران در زمینه های درخواستی دوره های موجود در وب سایت
باعث افتخارست که مجموعه ما تا کنون بیش از ۱۲۰۰ پروژه موفق در زمینه های متخلف ارائه نموده است که با مراجعه به بخش نمونه کارها در دسترس شما عزیزان قرار گرفته است. در صورتی که تصور می کنید پروژه مورد نظر شما در این دسته بندی ها قرار ندارد با تماس با تیم حرفه ای ما می توانید از مشاوره رایگان بهره مند گردید.

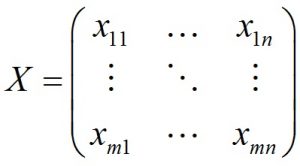
خیلی عالی بود
مراحل را بسیار واضح و خوب توضیح داده بودید
خواهش می کنم.