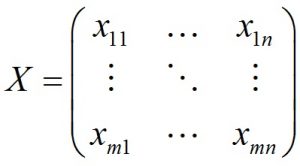آموزش صفر تا صد روش TOPSIS
روش TOPSIS یکی از روشهای تصمیم گیری چند شاخصه (MADM) است که به رتبه بندی گزینه ها می پردازد. در این روش از دو مفهوم “حل ایده آل” و “شباهت به حل ایده آل” استفاده شده است. حل ایده آل چنان چه از اسم آن پیداست، آن حلی است که از هر جهت بهترین باشد که عموما در عمل وجود نداشته و سعی بر آن است که به آن نزدیک شویم.
به منظور اندازه گیری شباهت یک طرح (یا گزینه) به حل ایده آل و ضد ایده آل، فاصله آن طرح (یا گزینه) از حل ایده آل و ضدایده آل اندازه گیری می شود. سپس گزینه ها بر اساس نسبت فاصله از حل ضد ایده آل به مجموع فاصله از حل ایده آل و ضد ایده آل ارزیابی و رتبه بندی می شوند. واژه TOPSIS از حروف اول عبارت Technique for Order of Preference by Similarity to Ideal Solution گرفته شده است.
آنچه می خوانید
روش TOPSIS (تاپسیس) چیست؟
TOPSIS یک مساله MADM با گزینه های m را به عنوان یک سیستم هندسی با نقاط m در فضای n بعدی مشاهده می کند. روش مبتنی بر این مفهوم است که گزینه جایگزین باید کمترین فاصله را از راه حل مثبت-ایده آل و طولانی ترین فاصله از راه حل منفی-ایده آل داشته باشد.
TOPSIS شاخصی به نام شباهت با راه حل مثبت- ایده آل و دوری از راه حل منفی-ایده آل را تعریف می کند. سپس روش جایگزین با حداکثر شباهت به راه حل مثبت-ایده آل را انتخاب می کند.
اگر گزینه ای شبیه به یک راه حل ایده آل باشد ، درجه بالاتری دارد. راه حل ایده آل یک راه حل است که از هر جنبه ای که به طور عملی وجود ندارد بهترین است و ما سعی می کنیم آن را تقریبی کنیم. اصولاً برای اندازه گیری شباهت یک طرح (یا گزینه) با سطح ایده آل و غیر ایده آل ، فاصله آن طرح را از راه حل ایده آل و غیر ایده آل در نظر می گیریم.
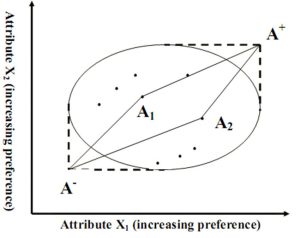
روش تاپسیس بر مبنای یک اصل شهودی در روانشناسی تصمیمگیری بنا شده است: انسانها همواره به دنبال گزینهای هستند که بیشترین شباهت را به «تصویر ذهنی ایدهآل» آنها داشته باشد. در ریاضیاتِ این روش، ما این تصویر ذهنی را به دو نقطه مرزی تبدیل میکنیم: یکی نقطه اوج (PIS) که تمام خوبیها را در خود دارد و دیگری نقطه حضیض (NIS) که مجموعهای از بدترین وضعیتهاست. فلسفه تاپسیس برخلاف روشهایی که تنها بر نزدیکی به هدف تمرکز دارند، بر این اصل استوار است که «دوری از بدترین» به اندازه «نزدیکی به بهترین» اهمیت دارد.
این رویکرد دوطرفه، یک «ناحیه اطمینان» برای تصمیمگیرنده ایجاد میکند. در بسیاری از مسائل واقعی، ممکن است گزینهای به ایدهآل مثبت بسیار نزدیک باشد، اما همزمان در یکی از معیارهای حیاتی، وضعیت بسیار خطرناکی داشته باشد که آن را به ایدهآل منفی نزدیک کند. تاپسیس با ترکیب این دو فاصله، مانع از انتخاب چنین گزینههای ریسکی میشود. در واقع، این روش به دنبال گزینهای است که یک توازن منطقی میان تمام معیارها برقرار کرده و از قطبیشدن شدید در نتایج جلوگیری کند.
مفروضات زیربنایی روش TOPSIS
- مطلوبیت هر معیار باید به طور یکنواخت، افزاینده و یا کاهنده باشد. به عبارت دیگر مطلوبیت معیار اعم از کیفی یا کمی با تغییر مقدار آن همواره افزاینده با کاهنده است. معیارها باید به طور یکنواخت کاهنده یا افزاینده باشند تا بتوان بهترین ارزش موجود آن را، ایده آل و بدترین ارزش آن را، ضد ایده آل تلقی کرد.
- معیارها باید به گونه ای طرح شوند که مستقل از همدیگر باشند (مستقل بودن به معنی عدم وجود روابط درونی می باشد).
- از آن جا که نرخ تبادل بين معیارها معمولا مقداری غیر از واحد است، فاصله گزینه ها از حل ایده آل و ضد ایده آل به صورت فاصله اقلیدسی محاسبه می شود.
نکته مهم: مواردی که در بیشتر موضوعات پروپوزال و پایان نامه ها مشاهده می شود این است که به عنوان مثال برای رتبه بندی عوامل و شاخص های پژوهش روش TOPSIS را انتخاب نموده اند، در صورتیکه این اشتباه است و روش TOPSIS فقط برای رتبه بندی گزینه های مساله مورد استفاده قرار میگیرد نه عوامل پژوهش.
به عنوان مثال فرض کنید موضوع پژوهشی در مورد مدیریت زنجیره تامین سبز است و میخواهیم با تکنیک TOPSIS این مساله را حل کنیم. این مساله تعدادی معیار که بر مدیریت زنجیره تامین سبز تاثیرگذار هستند انتخاب نموده است.
حال این معیارها را فقط با روشهایی نظیر آنتروپی، AHP، ANP و یا BWM قادر به وزن دهی و رتبه بندی هستیم در صورتیکه بخواهیم از روش TOPSIS استفاده کنیم باید برای مساله تعداد گزینه (آلترناتیو) تایین کنیم به عنوان مثال آلترناتیو ها می تواند تعداد شرکت باشد، تعدادی استراتژی باشند که هدف TOPSIS رتبه بندی این موارد می باشد نه رتبه بندی شاخص ها.
مزایای روش TOPSIS
- تصمیم گیری در صورت وجود معیارهای مثبت و منفی (حتی توام با هم در یک مساله) امکان پذیر است. معیارهای مثبت معیارهایی هستند گه جنبه سود دارند مثل کیفیت کالا و معیارهای منفی معیارهایی هستند که جنبه ضرر دارند مثل سختی کار.
- برای تعیین بهترین گزینه می توان تعداد قابل توجهی معیار را مورد بررسی قرار داد در حالی که در روش AHP یا روش ANP عملا و ذاتا در این زمینه محدودیت هایی وجود دارد.
- این روش ساده و دارای سرعت مناسب است و برای تعداد زیادی گزینه و معیار به خوبی پاسخگو است.
- در روش TOPSIS به راحتی می توان معیارهای کیفی را کمی کرد و تصمیم گیری با وجود معیارهای کیفی و کمی میسر است.
- خروجی سیستم به صورت کمی است و علاوه بر تعیین گزینه برتر، رتبه سایر گزینه ها به صورت عددی بیان می شود. این مقدار عددی همان نزدیکی نسبی است که پایه قوی این روش را بیان می کند.
- روش TOPSIS، دارای پایه های ریاضی مناسب است. این روش با فاصله ها سروکار دارد. TOPSIS گزینه ای را که بیشترین فاصله از بدترین گزینه و کمترین فاصله از بهترین گزینه دارد، به عنوان گزینة بهینه انتخاب می کند و به همین دلیل و پایة ریاضی اش، بر سایر روش های MADM برتری دارد.
- روش TOPSIS برتری دیگری نسبت به بعضی از روشهای MADM دارد که این روش از روش های جبرانی است. یعنی وزن تمامی گزینه ها و معیارها در تصمیم گیری دخالت داده می شود و هیچ وزنی در این روش نادیده گرفته نمی شود.
گام های روش TOPSIS
گام اول: تشکیل ماتریس تصمیم:
که در آن xij عملکرد گزینه i در رابطه با معیار j می باشد.
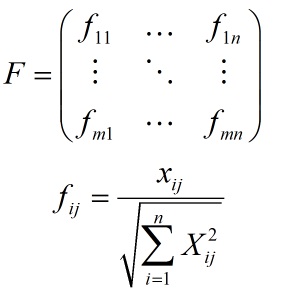
گام دوم: بی مقیاس کردن ماتریس تصمیم:
برای این کار روش های مختلفی وجود دارد اما معمولا از رابطه روبرو استفاده می شود که هر عدد تقسیم بر محموع ستونی می گردد.
گام سوم: تعیین بردار وزن معیارها [w=[w1,w2…wn
ضریب اهمیت معیارها توسط صورت مساله یا n به ما داده می شود.
گام چهارم: تعیین ماتریس تصمیم بی مقیاس شده وزن دار:
در این مرحله هر عنصر از ماتریس R را در وزن مربوطه شاخص ضرب می کنیم و در سرجایش در ماتریس قرار می دهیم.
Vij = wj rij i =1…n j=1…m
گام پنجم: یافتن حد ایده آل و ضد ایده آل:
در ماتریس به وجود آمده در مرحله قبل در هر ستون، اگر شاخص مربوطه از نوع سود است آن را یک شاخص مثبت در نظر می گیریم و گزینه ای را که دارای بیشترین مقدار Vij است به عنوان گزینه ایده آل آن شاخص و گزینه ای را که دارای کمترین Vij است به عنوان گزینه ضد ایده آل آن شاخص در نظر می گیریم.
در صوریکه شاخص از نوع هزینه است آن شاخص را از نوع منفی در نظر گرفته و گزینه ایده آل گزینه ای است که کمترین مقدار را در ستون مربوطه داشته باشد و همچنین گزینه ضد ایده آل گزینه ای است که بیشترین مقدار را در ستون مربوطه داشته باشد. نهایتا گزینه ایده آل هر ستون را با V*j و گزینه ضد ایده آل را با V–j نشان می دهیم.
گام ششم: محاسبه فاصله از حد ایده آل و ضد ایده آل:
در این مرحله برای هر گزینه به صورت سطری فاصله آن از حد ایده آل و ضد ایده آل از روابط زیر محاسبه می کنیم. روش کار بدین صورت است که به صورت سطری جلو می رویم و هر عدد را از ایده ال همان ستون کم می کنیم. سپس به سراغ عنصر بعدی در سطر مربوط به همان گزینه می رویم و ادامه می دهیم.
S*i= √∑(Vij – V*j)2 S–i= √∑(Vij – V–j)2
گام هفتم: محاسبه شاخص شباهت
برای هر گزینه شاخص شباهت را به صورت زیر محاسبه می کنیم:
C*i = S–i / S*i+ S–i
گام هشتم: رتبه بندی گزینه ها
بر اساس شاخص شباهت صورت می گیرد. بدین صورت که مقدا شاخص شباهت بین صفر و یک تغییر می کند. هرچه گزینه به ایده آل مشابه تر باشد شاخص شباهت به یک نزدیک تر خواهد بود.
مزایا و محدودیتهای TOPSIS؛ از دقت محاسباتی تا چالشهای ساختاری
بزرگترین مزیت روش تاپسیس، توانایی آن در مدیریت حجم عظیمی از دادهها بدون کاهش دقت ریاضی است. در بسیاری از روشهای MCDM مانند AHP، با افزایش تعداد گزینهها به بیش از ۱۰ مورد، ذهن خبره دچار خطا شده و نرخ ناسازگاری به شدت بالا میرود. اما در تاپسیس، فرقی نمیکند که شما ۵ گزینه دارید یا ۵۰۰ گزینه؛ الگوریتم ریاضی به طور یکنواخت عمل کرده و رتبهبندی کاملی را ارائه میدهد. این ویژگی، تاپسیس را به ابزاری بیرقیب در مسائل «غربالگری» (Screening) و انتخاب تأمینکنندگان در زنجیرههای تأمین بزرگ تبدیل کرده است.
علاوه بر این، تاپسیس به دلیل ساختار گامبهگام و شفاف، به راحتی در نرمافزارهایی مثل اکسل، متلب و پایتون قابل پیادهسازی است. این شفافیت باعث میشود مدیران غیرفنی نیز بتوانند منطق رتبهبندی را درک کرده و به نتایج اعتماد کنند. همچنین، در نظر گرفتن ماهیت معیارهای سود و هزینه به صورت مستقیم در مدل، باعث میشود که نیازی به تغییر دستی دادهها نباشد و مدل به صورت خودکار، تضاد بین معیارهایی مثل «افزایش کیفیت» و «کاهش قیمت» را مدیریت کند.
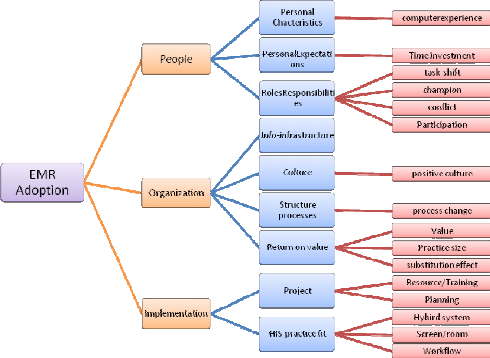
مزایا و محدودیتهای TOPSIS
با این حال، تاپسیس بدون نقص نیست. یکی از چالشهای اصلی این روش، حساسیت آن به روش «نرمالسازی» است. تحقیقات نشان داده که استفاده از نرمالسازی برداری در برابر نرمالسازی خطی میتواند رتبه گزینههای میانی را جابجا کند. همچنین، این روش فرض میکند که معیارها مستقل از یکدیگر هستند؛ در حالی که در دنیای واقعی، معیارها اغلب دارای همبستگی (Correlation) هستند. اگر دو معیار همبستگی بالایی داشته باشند، تاپسیس به طور ناخواسته وزن بیشتری به آن جنبه از مسئله میدهد که ممکن است منجر به سوگیری در رتبهبندی نهایی شود.
یکی دیگر از محدودیتهای کلاسیک که در مقالات اخیر بسیار بحث میشود، پدیده «واژگونی رتبه» (Rank Reversal) است. این پدیده زمانی رخ میدهد که با حذف یا اضافه کردن یک گزینه ضعیف، رتبه گزینههای برتر که اصلاً تغییری نکردهاند، با هم جابجا شود. این موضوع ناشی از تغییر در نقاط ایدهآل (PIS و NIS) است. برای حل این مشکل، محققان در سال ۲۰۲۶ پیشنهاد میدهند که نقاط ایدهآل به صورت «مطلق» یا «خارجی» تعریف شوند تا پایداری مدل در مواجهه با تغییر گزینهها حفظ شود.
تحلیل حساسیت در روش تاپسیس؛ آزمون تابآوری تصمیمات
در یک مقاله علمی معتبر، رتبهبندی نهایی تنها نیمی از راه است؛ نیمه دوم و مهمتر، اثبات اعتبار این رتبهبندی از طریق تحلیل حساسیت (Sensitivity Analysis) است. در روش تاپسیس، تحلیل حساسیت به ما میگوید که رتبه اول چقدر «شکننده» است. از آنجا که وزن معیارها معمولاً بر اساس نظرات ذهنی خبرگان است، همیشه این احتمال وجود دارد که قضاوتها کمی خطا داشته باشند. تحلیل حساسیت با تغییر سیستماتیک وزنها (مثلاً ۵٪ تا ۲۰٪ افزایش یا کاهش اهمیت یک معیار)، بررسی میکند که آیا گزینه برتر همچنان در جایگاه خود باقی میماند یا خیر.
این تحلیل معمولاً در قالب نمودارهای عنکبوتی (Spider Charts) یا نمودارهای میلهای انباشته ارائه میشود. اگر با تغییر جزئی در وزن یک معیار، رتبه اول و دوم جابجا شوند، اصطلاحاً گفته میشود که مدل «حساسیت بالایی» دارد و تصمیمگیرنده باید در جمعآوری دادههای آن معیار دقت بیشتری به خرج دهد. اما اگر رتبهها با وجود تغییرات وسیع در وزنها ثابت بمانند، خروجی تاپسیس «پایدار» و «قابل اتکا» تلقی میشود. این بخش از مقاله، اعتماد داوران را به یافتههای پژوهش جلب میکند، زیرا نشاندهنده دقت نظر محقق در مواجهه با عدم قطعیتهاست.
علاوه بر تغییر وزنها، نوع دیگری از تحلیل حساسیت در تاپسیس، تغییر در مقادیر عملکردی (دادههای ماتریس تصمیم) است. این کار به ویژه در مسائل اقتصادی که قیمتها نوسان دارند، بسیار حیاتی است. محقق با تعریف سناریوهای «خوشبینانه»، «واقعبینانه» و «بدبینانه»، خروجی Cl_i را برای هر سناریو محاسبه میکند. این رویکرد چندلایه به مدیران اجازه میدهد تا بدانند در بدترین شرایط بازار، کدام گزینه همچنان کمترین فاصله را از ایدهآل و بیشترین فاصله را از شکست دارد.
ادغام تاپسیس با منطق فازی؛ مدیریت ابهام در دنیای واقعی
در دنیای واقعی، جملات خبرگان معمولاً با شک و تردید همراه است؛ جملاتی مثل «قیمت تقریباً مناسب است» یا «کیفیت بسیار بالاست» را نمیتوان به سادگی با یک عدد قطعی در تاپسیس وارد کرد. اینجا جایی است که Fuzzy TOPSIS وارد عمل میشود. در این روش، اعداد قطعی جای خود را به اعداد فازی (معمولاً مثلثی یا ذوزنقهای) میدهند. این اعداد دارای سه وجه هستند: کمترین مقدار ممکن، محتملترین مقدار و بیشترین مقدار ممکن. این ساختار به خبره اجازه میدهد تا «بازه اطمینان» خود را در مدل لحاظ کند.
فرآیند تاپسیس فازی پیچیدهتر است، زیرا تمامی گامها از جمله نرمالسازی و محاسبه فاصله، باید بر اساس اصول محاسبات فازی انجام شود. در گام محاسبه فاصله، ما از متریکهای مخصوصی مانند «فاصله ورتکس» استفاده میکنیم تا فاصله بین دو عدد فازی را بسنجیم. خروجی نهایی این روش نیز یک عدد فازی است که در نهایت طی فرآیند «فازیزدایی» (Defuzzification) به یک عدد قطعی برای رتبهبندی تبدیل میشود. این روش برای مقالات ISI که با پرسشنامههای کیفی (طیف لیکرت) کار میکنند، یک ضرورت محسوب میشود.
در سالهای اخیر و به ویژه در سال ۲۰۲۶، گرایش به سمت مدلهای پیشرفتهتر مانند Intuitionistic Fuzzy TOPSIS افزایش یافته است. این مدلها نه تنها «میزان موافقت» خبره، بلکه «میزان مخالفت» و «تردید» او را هم به صورت جداگانه فرموله میکنند. استفاده از چنین رویکردهایی در مقاله، سطح علمی کار را از یک تحلیل ساده به یک پژوهش پیشرو در مرزهای دانش تصمیمگیری ارتقا میدهد. با این کار، شما به داور ثابت میکنید که مدل شما قدرت هضم پیچیدگیهای ذهنی انسان و تضادهای اطلاعاتی را دارد.
سوالات متداول درباره روش TOPSIS
۱. آیا میتوان از تاپسیس برای وزندهی معیارها استفاده کرد؟
خیر، تاپسیس یک روش “رتبهبندی گزینهها” است و وزنها باید از روشهای دیگر وارد آن شوند.
تفاوت تاپسیس با روش VIKOR چیست؟
ویکور بر پایه “بیشترین سود گروهی” و “کمترین تأسف فردی” است، اما تاپسیس صرفاً بر پایه “فاصله هندسی” کار میکند.
آیا در تاپسیس تعداد معیارها محدودیت دارد؟
خیر، یکی از نقاط قوت تاپسیس هندل کردن تعداد زیادی از معیارها و گزینهها بدون پیچیدگی محاسباتی است.
چرا گاهی رتبهها در تاپسیس منطقی نیستند؟
این معمولاً به دلیل نرمالسازی اشتباه یا وجود دادههای بسیار پرت (Outliers) است که ایدهآلها را به شدت منحرف میکنند.
چرا داوران ISI هنوز به تاپسیس علاقه دارند؟
چون این روش یک “مبنای مقایسه” (Baseline) عالی است. معمولاً محققان روشهای جدید خود را با نتایج تاپسیس مقایسه میکنند تا صحت آنها را تایید کنند.
این