روش جستجوی طلایی
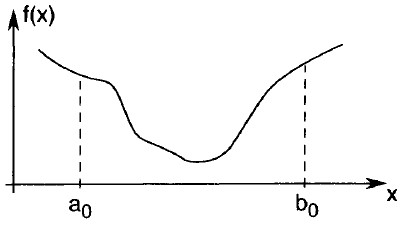
روش های جستجویی که ما در این بخش و بخش بعدی مورد بحث قرار می دهیم به منظور تعیین کمینه تابع f: R-> R بر روی بازه بسته بکار می رود به طوری که [a0 ,b0] . تنها ویژگی که ما برای تابع هدفf فرض می نماییم تک مدی بودن آن است، به این معنی که f فقط داری یک مینیمم محلی است. مثالی از چنین تابعی در شکل روبرو نشان داده شده است.
روش جستجوی طلایی
روش جستجوی طلایی در مورد ارزیابی تابع هدف در نقاط مختلف بازه [a0 ,b0] می باشد. این نقاط را چنان انتخاب می نماییم که یک تقریب ممکن به نقطه کمینه را با چند ارزیابی ممکن به دست آورد . هدف محدود کردن تدریجی دامنه با دقت کافی به منظور قرار گرفتن کمینه در بازه مد نظر می باشد.
تابع تک مدی f را با یک متغیر و بازه [a0 ,b0] در نظر بگیرید. اگر f را فقط در یک نقطه میانی از بازه در نظر بگیریم قادر نخواهیم بود در میان این طیف گسترده کمینه را قرار دهیم لذا باید به منظور ارزیابی f تابع را در دو نقطه میانی همانطور که در شکل زیر نشان داده شده است در نظر بگیریم.
روش جستجوی طلایی
نقاط میانی را چنان انتخاب می نماییم که کاهش در محدوده متقارن باشد، به این معنا که
a1 – a0 = b0 – b1 = p (b0 – a0) به طوری که p< 0.5
سپس به ارزیابی تابع f در نقطه میانی می پردازیم. اگر f(a1)<f(b1) باشد، کمینه در بازه [a0, b1] نهفته است. از سوی دیگر، اگر (f(a1)≥f(b1 باشد، کمینه در بازه [a1, b0] قرار گرفته است. درادامه با کاهش دامنه عدم قطعیت، ما می توانیم این روند را تکرار و به همین ترتیب دو نقطه جدید a2 و b2 را با مقدار p=0.5 پیدا نماییم. در عین حال، ما علاقمندیم که تعداد ارزیابی تابع هدف را در حالی که بازه عدم قطعیت را کاهش می دهیم کمینه نماییم.
روش جستجوی طلایی
برای مثال فرض کنید که (f(a1)<f(b1 باشد. ما می دانیم نقطه بهینه x* متعلق به بازه [a0, b1] خواهد بود. از آنجا که a1 در حال حاضر در فاصله عدم اطمینان است و f تابعی شناخته شده، می توانیم a1 را با b2 یکی و منطبق بر هم در نظر بگیریم. بنابراین، تنها یک ارزیابی جدید از تابع f در نقطه a2 ضروری خواهد بود. برای پیدا کردن مقدار p که منجر به تنها یک ارزیابی جدید گردد شکل زیر را مشاهده نمایید.
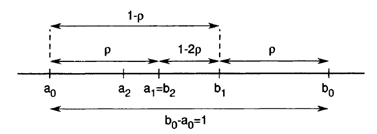
بدون از دست دادن کلیت، تصور کنید که محدوده اصلی [a0 ,b0] طول واحد است. لذا به منظور داشتن تنها یک ارزیابی از f کافی است که p مناسب را انتخاب نماییم.
P (b1– a0) = b1 – b2
از آنجایی که مقدار b1 – b0 = 1- p و مقدار b1 – b2 = 1 -2p می باشد، لذا خواهیم داشت:
P (1 – p) = 1 – 2p *
تابع درجه دوم عبارت فوق را به صورت زیر می نویسیم:
P2‑3p+1=0 -> p1 = (3+√5)/2 , p2 = (3-√5)/2
از آنجایی که مقدار p<0.5 را نیاز خواهیم داشت مقدار p2 =0.382 را در نظر می گیریم. با جایگزینی مقدار تابع در عبارت * مشاهده می کنیم که p/(1-P) = (1-p)/1 خواهد بود. از این عبارت در یونان باستان به عنوان قانون طلایی یاد شده است.
استفاده از بخش قانون طلایی بدان معنی است که در هر مرحله از کاهش دامنه عدم قطعیت (به جز بازه اول)، تابع هدف f تنها نیاز به ارزیابی در یک نقطه جدید را دارد. یعنی در هر مرحله از کاهش، محدوده عدم قطعیت با نرخ –p = 0.61803 1 کاهش می یابد. از این رو، N مرحله کاهش با استفاده از روش طلایی با نرخ زیر کاهش خواهد یافت:
(1 – p)N = (0.61803)N