روش مورا فازی
بهینه سازی چند هدف بر اساس تحلیل نسبت (MOORA)، فرایند بهینه سازی دو یا چند ویژگی متضاد است که به
طور همزمان در معرض محدودیت های خاصی هستند (Brauers & Zavadskas، 2006).
بنابراین ، به نظر می رسد این روش ابزاری مناسب برای ارزیابی رتبه بندی یا انتخاب بهترین گزینه از مجموعه
گزینه های امکان پذیر است.
این روش به دلیل جامع بودن و سادگی آن در بسیاری از زمینه های مهندسی سازه (Chakraborty، 2011)، مهندسی ساخت و مدیریت (Kracka et al، 2015؛ Brauers et al.، 2008)
و همچنین در اقتصاد (Brauers & Ginevicious، 2009، کاربرد موفقیت آمیزی داشته است.
در این روش مقادیر اهداف برای هر گزینه جایگزین می شود و این زمینه را برای مقایسه گزینه های مختلف
فراهم می کند و در نتیجه انتخاب بهترین (رضایت بخش ترین) گزینه را تسهیل می کند.
روش مورا فازی
منطق اصلی روش مورا محاسبه عملکرد کلی هر یک از گزینه ها براساس تفاوت میان عملکردهای عادی آن از
معیارهای مفید و غیر مفید با استفاده از معادله زیر است:
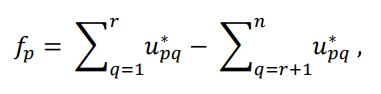
که در آن U*pq یک عدد بدون بعد است، به بازه [0 ، 1] تعلق دارد و عملکرد عادی p امین جایگزین را در q امین معیار نشان می دهد،
r تعداد معیاری است باید حداکثر شود (معیارهای مفید) و (n-r) تعداد معیارهای است که باید حداقل شوند
(معیارهای غیر مفید) و fp ارزش کل شاخص های عملکرد p امین جایگزین با توجه به سایر خصوصیات است.
ممکن است اولویت وزنی در نظر گرفته شود که اهمیت نسبی یک معیار را نسبت به دیگری نشان می دهد، زیرا
به طور کلی مشاهده می شود که برخی از معیارها از سایرین اهمیت بیشتری دارند.
هنگامی که وزن های اولویتی مورد توجه قرار می گیرند، معادله بالا را می توان به صورت زیر نوشت:
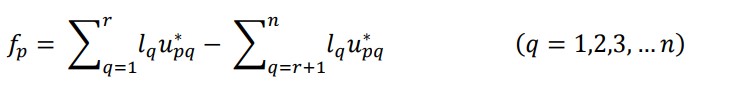
در آن ، lq وزن q امین ویژگی است که ممکن است با روش آنتروپی شانون یا تحلیل سلسله مراتبی (AHP) حاصل شود.
ترجیحات نهایی را می توان با رتبه بندی معمولی fp پیدا کرد. بالاترین مقدار با بهترین جایگزین مطابقت دارد در
حالی که کمترین مقدار مربوط به بدترین گزینه است.
گام های روش
مرحله 1: ابتدا یک ماتریس تصمیم گیری فازی را بر اساس نظرات تصمیم گیرندگان کلیدی تهیه کنید که در آن هر
معیار با استفاده از تابع عضویت مثلثی اندازه گیری می شود.
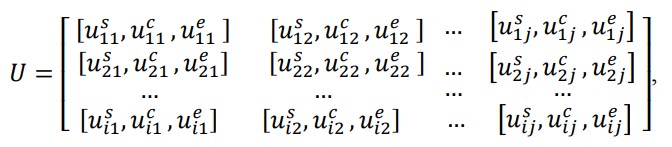
که در آن Uspq و Ucpq و Uepq مقادیر پایین ، متوسط و بالایی یک تابع عضویت مثلثی را برای جایگزین p ام با توجه به معیارهای qام بیان می کنند.
مرحله 2: با استفاده از روال نرمال سازی بردار ، ماتریس تصمیم گیری فازی ، ایجاد شده در مرحله 1 را نرمال کنید. برای این منظور از معادلات زیر استفاده می شود (Stanujkic et al.، 2012).
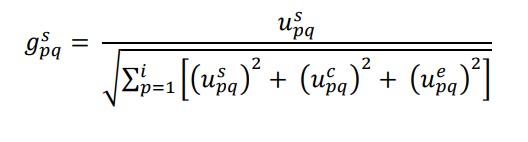
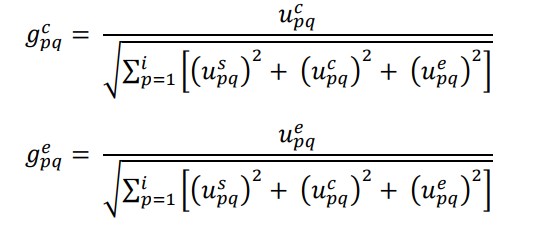
روش مورا فازی
مرحله 3: ماتریس تصمیم گیری فازی با وزنه نرمال با معادلات زیر تعیین می شود ،
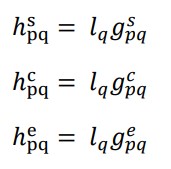
مرحله 4: در این مرحله رتبه بندی های کلی معیارهای مفید و غیر مفید برای هر گزینه محاسبه می شود.
امتیاز کلی گزینه جایگزین برای مقادیر پایین ، متوسط و بالای عملکرد مثلثی برای معیارهای مفید توسط معادلات زیر تعیین می شود ،
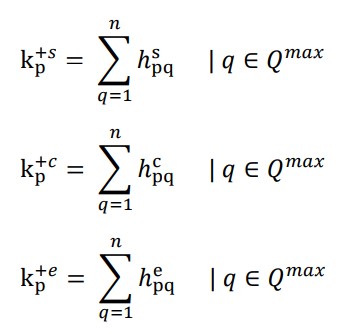
امتیاز کلی گزینه جایگزین برای مقادیر پایین ، متوسط و بالای عملکرد مثلثی برای معیارهای غیر مفید توسط معادلات زیر تعیین می شود ،
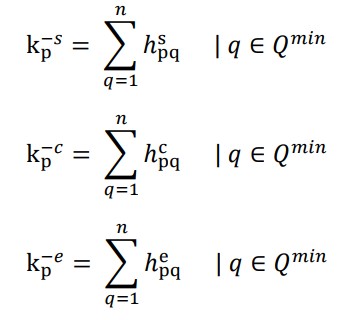
مرحله 5: در این مرحله مقادیر رتبه بندی کلی را برای معیارهای مفید و غیر مفید برای هر گزینه را با استفاده از روش ورتکس (Huiqun & Guang، 2012) مشخص کرده و شاخص کل عملکرد (Si) را تعیین می کنید.
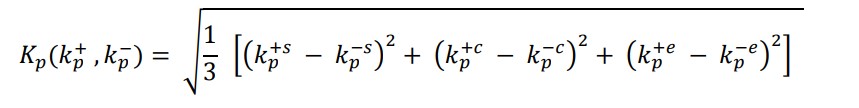
روش مورا فازی روش مورا فازی روش مورا فازی روش مورا فازی
مرحله ششم: اکنون شاخص های کلی عملکرد را به ترتیب نزولی ترتیب داده و آنها را از بهترین به بدترین رتبه قرار دهید. گزینه جایگزین با بالاترین شاخص عملکرد کلی ، مطلوب ترین گزینه است.
مثال روش مورا فازی
این مثال از مقاله Application of fuzzy-MOORA method: Ranking of components for reliability estimation of component-based software systems استخراج شده است.
در این مطالعه موردی ، ما یک سیستم مدیریت امنیتی مبتنی بر مؤلفه کوچک ارائه شده توسط تایگی و شارما 2014 را در نظر گرفتیم.
این سیستم در مجموع هشت مولفه دارد:
(1) ورود به سیستم (2) سرور (3) سیستم مدیریت زمان (4) سیستم مدیریت زنگ هشدار (5) سیستم مدیریت دسترسی (6) اسکریپت محاسبه (7) سیستم مدیریت درها و (8) دستگاه ها. این مؤلفه ها به عنوان گزینه های جایگزین برای رتبه بندی در نظر گرفته می شوند.
هدف ما استفاده از روش پایدار و قوی مورا فازی برای ارزیابی و سنجش رتبه بندی مؤلفه ها برای برآورد قابلیت اطمینان این سیستم می باشد.
در این مثال اوزان شاخص ها از طریق روش AHP محاسبه شده و به ترتیب برابر Lc1 = 0.2629, Lc2 = 0.2280, Lc3 = 0.2629, Lc4 = 0.2462 می باشد.
گام اول: ماتریس تصمیم گیری
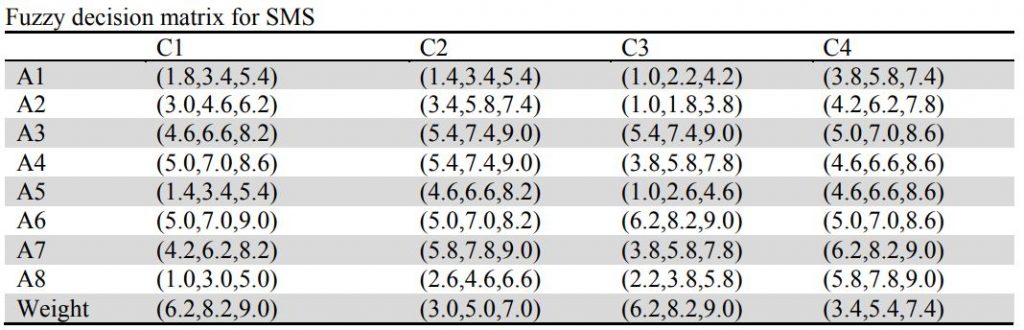
گام دوم: ماتریس تصمیمی نرمال سازی شده
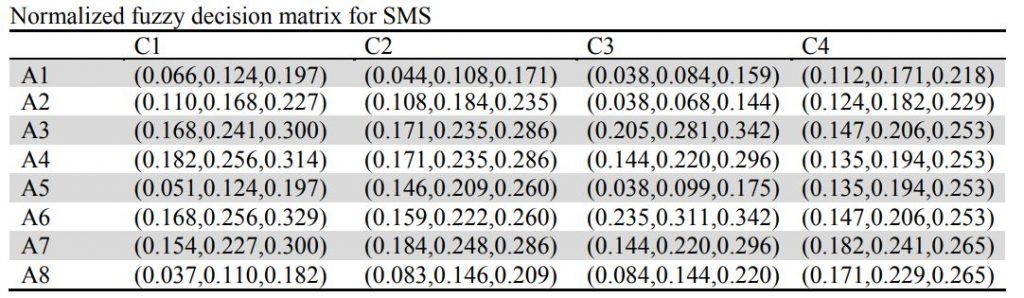
گام سوم: ضرب اوزان در ماتریس نرمال شده
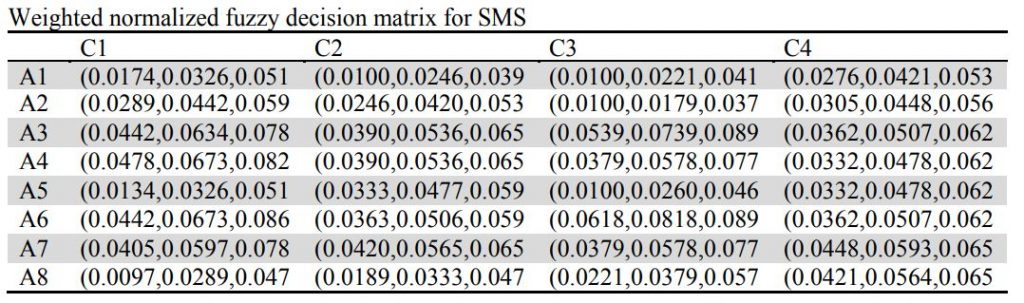
گام چهارم: محاسبه مقادیر مفید و غیرمفید. در اینجام فقط شاخص اول غیرمفید (حداقل) و سایر شاخص ها مفید هستند پس مفید ها باهم جمع و از غیر مفید کم می شوند تا ماتریس کلی بدست آید
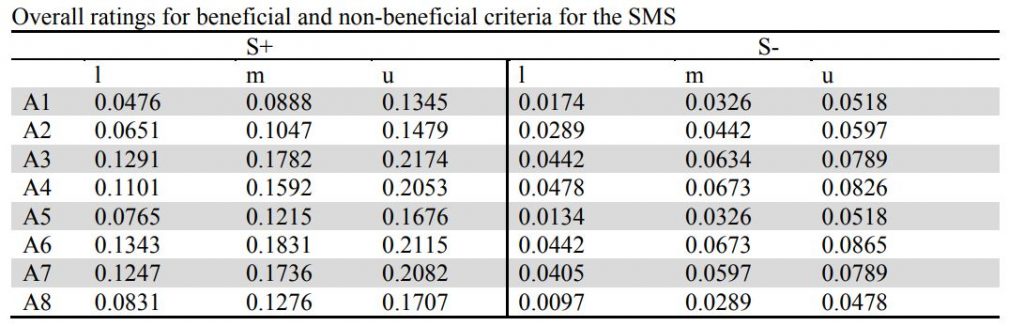
گام پنجم: بر اساس روش ورتکس (vertex) اعداد محاسبه و رتبه بندی می شود.