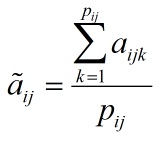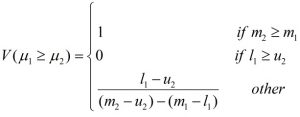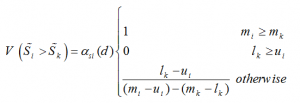آموزش جامع روش AHP فازی
در دنیای واقعی، ذهن انسان همیشه با قطعیت ریاضی (اعداد ۱ تا ۹) کار نمیکند. روش روش AHP قطعی، خبره را مجبور میکند تا یک عدد دقیق برای ترجیحات خود انتخاب کند، اما در بسیاری از مسائل تصمیمگیری چندمعیاره (MCDM)، پاسخها با ابهام همراه هستند. روش AHP فازی با معرفی بازههای عددی، به خبره اجازه میدهد تا تردید خود را در مدل ریاضی لحاظ کند و بدین ترتیب، نتایج حاصله به واقعیت ذهن انسان نزدیکتر میشود.
این رویکرد در پژوهشهای تحقیق در عملیات به عنوان ابزاری برای کاهش ریسک قضاوت شناخته میشود. وقتی از اعداد فازی (مثلثی یا ذوزنقهای) استفاده میکنیم، در واقع یک حاشیه امنیت برای تصمیمگیری ایجاد کردهایم. اگر در یک پایاننامه مدیریتی یا مهندسی، دادهها کیفی و مبتنی بر حدس و گمان باشند، استفاده از مدل فازی به جای مدل قطعی، اعتبار علمی بخش آمار و تحلیل داده را به شدت افزایش میدهد و نشاندهنده دقت محقق است.
ما در سایت فرابگیر معتقدیم که آموزش مدیریت مدرن بدون درک مفاهیم فازی ناقص است. روش AHP فازی (FAHP) نه تنها ابهام را مدیریت میکند، بلکه از سوگیریهای ناشی از اجبار خبره به انتخاب یک عدد واحد جلوگیری میکند. این روش به ویژه در پروژههای استراتژیک، ارزیابی ریسک و انتخاب تکنولوژی که آینده آنها شفاف نیست، به عنوان استاندارد طلایی شناخته میشود.
آنچه می خوانید
چرا به جای AHP از AHP فازی استفاده میکنیم؟
روش AHP فازی در واقع فازی سازی روش تحلیل سلسله مراتبی کلاسیک است. با توجه به این امر ابتدا تحلیل سلسله مراتبی را تبیین می کنیم و پس از آن مراحل تحلیل سلسله مراتبی فازی را با مثالی ملموس اجرا می کنیم.
فرآیند تحلیل سلسله مراتبی (AHP) برای تصمیمگیری با معیارهای چندگانه بهکار میرود زیرا با استفاده از این مدل میتوان معیارها را به صورت سلسله مراتبی با هم مقایسه کرد. این معیارها میتوانند کمی و یا کیفی باشند. تحلیل سلسله مراتبی (AHP) توسط توماس ال، ساعتی در دهه 1970 ارائه شده است. روش AHP فازی بر اساس مقایسات زوجی انجام میشود.
به عنوان مثال میخواهیم چندین مکان را برای احداث سالن ورزشی با هم مقایسه کنیم. این مکانها دارای ویژگیهای متفاوت هستند. تمام معیارهایی که برای انتخاب یک سالن ورزشی مناسب باید در نظر گرفته شود را بررسی کردهایم.
میخواهیم با استفاده از این معیارها زمینهای مناسب را شناسایی و اولویت بندی کنیم. برای اینکار از روش تحلیل سلسله مراتبی استفاده میکنیم و با توجه به نظرات خبرگان تصمیمگیری چندمعیاره را انجام میدهیم.
روش AHP فازی چیست؟
فرآیند تحلیل سلسله مراتبی فازی (FAHP) عبارتست از فازی سازی روش AHP کلاسیک با استفاده از اعداد و محاسبات فازی. هنگامی که اولویتها عدم اطمینان و عدم دقت را نشان میدهند، اعداد قطعی و دقیق برای نشان دادن قضاوت زمانی خیلی مناسب نیست.در جهت مقابله با ابهام، اعداد فازی مثلثی و AHP در روش فازی برای حل تصمیمگیری مسائل ادغام شدهاند.
برای برخورد با ابهام موجود در نظرات انسانها، لطفی عسگرزاده در سال ۱۹۶۵، نظریه مجموعههای فازی را ارائه داد تا عدم قطعیتی را که به علت ابهام و عدم دقت در رویدادها ایجاد شده است، تحت مدل درآورد. چانگ در سال ۱۹۹۲ روشی بسیار ساده را برای بسط فرآیند تحلیل سلسله مراتبی به فضای فازی ارائه داد.
روش AHP فازی که مبتنی بر میانگین حسابی نظرات خبرگان و روش نرمالسازی ساعتی و با استفاده از اعداد مثلثی فازی توسعه داده شده بود، مورد استقبال محققان قرار گرفت. با یک مثال ساده سلسله مراتبی فازی را بیشتر توضیح میدهیم.
فرض کنید برای اولویت بندی دروس دانشجویان معیارهایی وجود دارد، اما برای این معیارها اعداد قطعی جوابگو نیستند، پس ناچاریم از اعداد غیر قطعی یا فازی استفاده کنیم.
انواع روش AHP فازی
همانطور که AHP روش های مختلفی دارد، AHP فازی نیز دارای تنوع هایی است که هر کدام برای موقعیت های خاصی مناسب هستند. در اینجا به برخی از متداول ترین انواع AHP فازی اشاره می کنیم:
- روش چانگ: این روش که توسط Chang در سال 1992 توسعه یافته است، یکی از محبوب ترین روش های AHP فازی است. از میانگین حسابی اعداد فازی مثلثی برای محاسبه وزن معیارها و اولویت جایگزین ها استفاده می کند.
- روش بوکلی: این روش توسط Buckley در سال 1985 توسعه یافته است و از میانگین هندسی اعداد فازی مثلثی برای محاسبه وزن ها و اولویت ها استفاده می کند.
- روش میانگین هندسی فازی: این روش از میانگین هندسی اعداد فازی برای محاسبه وزن ها و اولویت ها استفاده می کند. این روش به ویژه زمانی مفید است که عدم قطعیت در قضاوت ها زیاد باشد.
- روش اعداد فازی بازه ای: این روش از اعداد فازی بازه ای برای نشان دادن مقایسه های جفت بین معیارها و جایگزین ها استفاده می کند. این روش برای موقعیت هایی که محدوده دقیق ترجیحات مشخص است مفید است.
- روش اعداد فازی مرتب شده: این روش از اعداد فازی مرتب شده برای نشان دادن مقایسه های جفت بین معیارها و جایگزین ها استفاده می کند. این روش برای موقعیت هایی که ترتیب ترجیحات مشخص است اما مقادیر دقیق نامشخص است مفید است.
- روش فازی ترکیبی: این روش از ترکیبی از روش های مختلف AHP فازی برای محاسبه وزن ها و اولویت ها استفاده می کند. این روش می تواند برای موقعیت هایی که نیاز به انعطاف پذیری بیشتر در نحوه مدل سازی عدم قطعیت دارند مفید باشد.
انتخاب نوع AHP فازی مناسب برای یک موقعیت خاص به عوامل مختلفی از جمله ماهیت تصمیم، در دسترس بودن داده ها و ترجیحات تصمیم گیرنده بستگی دارد.
در ادامه روش AHP فازی چانگ را تشریح خواهیم کرد.
مراحل انجام روش AHP فازی
مرحله ۱: ترسیم درخت سلسله مراتبی
در این مرحله ابتدا ساختار سلسله مراتبی تصمیم با استفاده از سطوح هدف، معیار و زیرمعیارها ترسیم میشود.
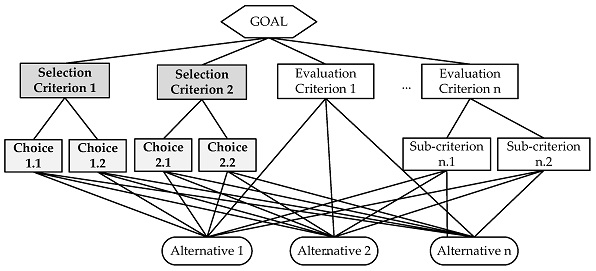
مرحله۲: تعریف اعداد فازی
بهمنظور انجام مقایسههای زوجی اعداد فازی را تعریف می کنیم. می توان نظر خبرگان را در قالب عباراتی مانند: مهم تر، خیلی مهم تر و… دریافت کرد و سپس آنها را با استفاده از جدول زیر به اعداد فازی مثلثی تبدیل نمود.
| عبارت کلامی | عدد فازی مثلثی | عدد فازی معکوس |
| اهمیت دقیقا مساوی | (1و1و1) | (1و1و1) |
| کمی مهم تر | (2/3و1و2/1) | (2و1و3/2) |
| مهم تر | (2و2/3و1) | (1و3/2و2/1) |
| خیلی مهم تر | (2/5و2وو2/3) | (3/2و2/1و5/2) |
| خیلی زیاد مهم تر | (3و2/5و2) | (2/1و5/2و3/1) |
| کاملا مهم تر | (2/7و3و2/5) | (5/2و3/1و7/2) |
مرحله۳: تشکیل ماتریس مقایسات زوجیa
در این مرحله ماتریسهای توافقی را مطابق با درخت تصمیم و با استفاده از نظرات خبرگان تشکیل داده و سپس نرخ ناسازگاری مطابق روش گوگوس و بوچر محاسبه میگردد. ماتریس مقایسه زوجی بهصورت زیر خواهد بود:
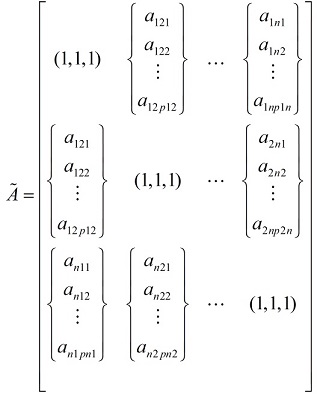
در این قسمت می توانید نحوه محاسبه نرخ ناسازگاری را مشاهده نمایید.
زمانی که بیش از یک خبره جداول نظرات را پر می نماید، می بایست از میانگین حسابی برای تجمیع نظرات تصمیم گیرندگان استفاده نمود. این میانگین را به صورت زیر محاسبه می کنیم:
مرحله۴: محاسبه Si
مقدار Si برای هر یک از سطرهای ماتریس مقایسه زوجی که خود یک عدد فازی مثلثی است از رابطه زیر محاسبه میشود:
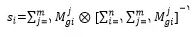
که در این رابطه i بیانگر شماره سطر و j بیانگر شماره ستون میباشد.mjgi در این رابطه اعداد فازی مثلثی ماتریسهای مقایسه زوجی هستند. سایر مقادیر را میتوان به ترتیب از روابط زیر محاسبه کرد:
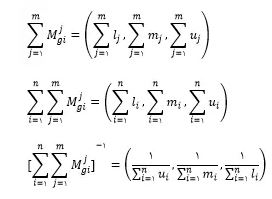
در روابط بالا li,mi,ui به ترتیب مولفههای اول تا سوم اعداد فازی هستند.
مرحله ۵: محاسبه درجه بزرگی si ها نسبت به همدیگر
به طور کلی اگرM1=(l1,m1,u1) و M2=(l2,m2,u2) دو عدد فازی مثلثی باشند، طبق ماتریس مقایسه زوجی درجه بزرگی m1 نسبت بهm2 به صورت زیر تعریف میشود:
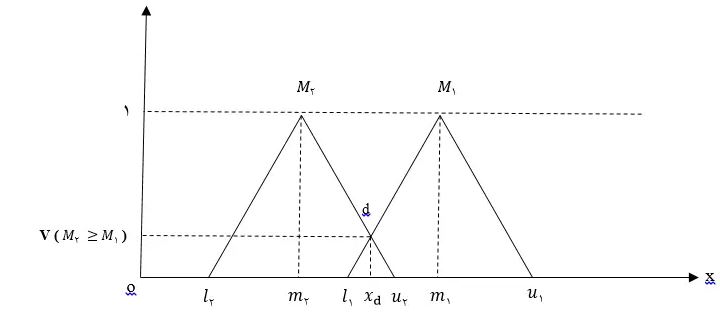
از طرف دیگر میزان بزرگی یک عدد فازی مثلثی از K عدد فازی مثلثی دیگر از رابطه زیر به دست میآید:
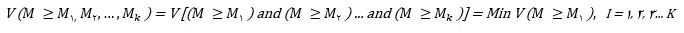
مرحله ۶: محاسبه وزن معیارها و گزینهها
برای محاسبه وزن معیارها و گزینهها در ماتریسهای مقایسه زوجی از رابطه زیر استفاده میشود:
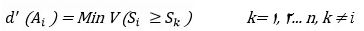
بنابراین بردار وزن نرمالسازی نشده به صورت زیر خواهد بود:
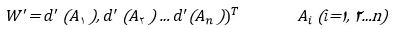
مرحله ۷: محاسبه بردار وزن نهایی
برای محاسبه بردار وزن نهایی باید بردار وزن محاسبه شده در مرحله قبل را نرمالسازی کرد بنابراین:
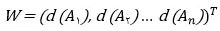
سایر مراحل مشابه روش تحلیل سلسله مراتبی کلاسیک خواهد بود. ما در سایت فرابگیر معتقدیم که آموزش مدیریت مدرن بدون درک مفاهیم فازی ناقص است. روش AHP فازی (FAHP) نه تنها ابهام را مدیریت میکند، بلکه از سوگیریهای ناشی از اجبار خبره به انتخاب یک عدد واحد جلوگیری میکند. این روش به ویژه در پروژههای استراتژیک، ارزیابی ریسک و انتخاب تکنولوژی که آینده آنها شفاف نیست، به عنوان استاندارد طلایی شناخته میشود.
مثال روش AHP فازی
یک تصمیم گیرنده قصد دارد جهت اعلام دانشکده برتر از بین دو دانشکده علوم پایه و مهندسی با توجه به سطح کیفی آن ها با این فرض که کیفیت دانشکده ها از کیفیت چهار عامل دانشجو، استاد، امکانات و مدیریت ناشی می شوند، با روش AHP فازی تصمیم گیری نماید.
گام اول: یک سلسله مراتب برای مساله می سازیم.
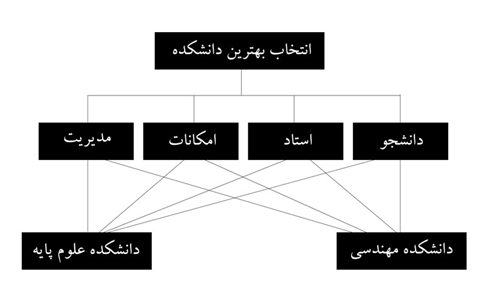
گام دوم: تعیین ماتریس مقایسات زوجی و اعمال قضاوت ها:
ماتریس مقایسه زوجی معیارها نسبت به هدف در جدول زیر آورده شده است.
| Q | دانشجو | استاد | امکانات | مدیریت | ||||||||
| دانشجو | 1 | 1 | 1 | 1/2 | 2/3 | 1 | 1 1/2 | 2 | 2 1/2 | 2/5 | 1/2 | 2/3 |
| استاد | 1 | 1 1/2 | 2 | 1 | 1 | 1 | 1 1/2 | 2 | 2 1/2 | 2/3 | 1 | 2 |
| امکانات | 2/5 | 1/2 | 2/3 | 2/5 | 1/2 | 2/3 | 1 | 1 | 1 | 1/3 | 2/5 | 1/2 |
| مدیریت | 1 1/2 | 2 | 2 1/2 | 1/2 | 1 | 1 1/2 | 2 | 2 1/2 | 3 | 1 | 1 | 1 |
ماتریس مقایسات زوجی گزینه ها نسبت به هریک از معیارها در جداول بعدی نشان داده شده است.
| P1: استاد | دانشکده مهندسی | دانشکده علوم پایه | P2: مدیریت | دانشکده مهندسی | دانشکده علوم پایه | |||||||||
| دانشجو | 1 | 1 | 1 | 2/3 | 1 | 2 | دانشجو | 1 | 1 | 1 | 1/2 | 2/3 | 1 | |
| استاد | 1/2 | 1 | 1 1/2 | 1 | 1 | 1 | استاد | 1 | 1 1/2 | 2 | 1 | 1 | 1 | |
| P3: دانشجو | دانشکده مهندسی | دانشکده علوم پایه | P4: امکانات | دانشکده مهندسی | دانشکده علوم پایه | |||||||||
| دانشجو | 1 | 1 | 1 | 1 | 1 1/2 | 2 | دانشجو | 1 | 1 | 1 | 2/3 | 1 | 2 | |
| استاد | 1/2 | 2/3 | 1 | 1 | 1 | 1 | استاد | 1/2 | 1 | 1 1/2 | 1 | 1 | 1 | |
گام سوم: محاسبه وزن های معیارها و گزینه ها
در مرحله اول، با استفاده از آنالیز توسعه ی چانگ، وزن های نسبی معیارها و گزینه ها را محاسبه می کنیم.
∑Mjg1= (1, 1, 1) + (1/2, 2/3, 1) + (3/2, 2, 5/2) + (2/5, 1/2, 3/2) = (3.4, 4.17, 5.17)
∑Mjg2= (4.17, 5.50, 7.50) | ∑Mjg3= (2.13, 2.40, 2.83) | ∑Mjg4= (5, 6.5, 8)
∑∑Mjgi = (3.4, 4.17, 5.17)+(4.17, 5.50, 7.50)+(2.13, 2.40, 2.83)+(5, 6.5, 8)=(14.7, 18.57, 23.5)
[∑∑Mjgi]-1= [1/23.5 , 1/18.57, 1/14.7] = (0.043, 0.054, 0.068)
S1 = (3.4, 4.17, 5.17) * (0.043, 0.054, 0.068) = (0.145, 0.224, 0.351)
S2 = (4.17, 5.50, 7.50) * (0.043, 0.054, 0.068) = (0.177, 0,296, 0.510)
S3 = (2.13, 2.40, 2.83) * (0.043, 0.054, 0.068) = (0.091, 0.129, 0.193)
S4 = (5, 6.5, 8) * (0.043, 0.054, 0.068) = (0.213, 0.350, 0.544)
و به همین ترتیب برای 4 ماتریس مقایسه زوجی p1, p2, p3, p4 مقادیر زیر بدست می آیند:
| P1 | ضرب در معکوس -استاد | P2 | ضرب در معکوس – مدیریت | ||||
| S1 | 0.303 | 0.500 | 0.947 | S1 | 0.300 | 0.400 | 0.571 |
| S2 | 0.273 | 0.500 | 0.789 | S2 | 0.400 | 0.600 | 0.857 |
| P3 | ضرب در معکوس – دانشجو | P4 | ضرب در معکوس – امکانات | ||||
| S1 | 0.400 | 0.600 | 0.857 | S1 | 0.303 | 0.500 | 0.947 |
| S2 | 0.300 | 0.400 | 0.571 | S2 | 0.273 | 0.500 | 0.789 |
در مرحله دوم محاسبه درجه ی ارجحیت درجه امکان پذیری Si بر Sk را بدست می آوریم.
S1 = (0.145, 0.224, 0.351) S2 = (0.177, 0,296, 0.510)
V (S1≥S2) = (0.177-0.351) / (0.224-0.351)-(0.296-0.177) = 0.708
V (S1≥S3) = 0.224 > 0.129 = 1
به همین منوال سایر مقایسات انجام می پذیرد.
| مقایسات زوجیQ | مقایسات زوجیQ | ||
| V(S1>S2) | 0.708 | V(S2>S1) | 1.000 |
| V(S1>S3) | 1.000 | V(S2>S3) | 1.000 |
| V(S1>S4) | 0.525 | V(S2>S4) | 0.847 |
| MIN | 0.525 | MIN | 0.847 |
| مقایسات زوجیQ | مقایسات زوجیQ | ||
| V(S3>S1) | 0.336 | V(S4>S1) | 1.000 |
| V(S3>S2) | 0.085 | V(S4>S2) | 1.000 |
| V(S3>S4) | 0.000 | V(S4>S3) | 1.000 |
| MIN | 0.000 | MIN | 1.000 |
| مقایسات زوجی P1 | مقایسات زوجیP2 | ||
| V(S1>S2) | 1 | V(S1>S2) | 0.462 |
| V(S2>S1) | 1 | V(S2>S1) | 1 |
| MIN | 1 | MIN | 0.462 |
| مقایسات زوجیP3 | مقایسات زوجیP4 | ||
| V(S1>S2) | 1 | V(S1>S2) | 1 |
| V(S2>S1) | 0.46 | V(S2>S1) | 1 |
| MIN | 0.46 | MIN | 1 |
V(S1≥S2, S3, S4) = min { V(S1≥S2), V(S1≥S3), V(S1≥S4)} =min {0.708,1 , 0.521 } = 0.52
V(S2≥S1, S3, S4) = min {0.708,1 , 0.521 } = 0.85
V(S3≥S1, S2, S4) = min {0.708,1 , 0.521 } = 0.00
V(S4≥S1, S2, S3) = min {0.708,1 , 0.521 } = 1.00
پس از محاسبه مقدار W’ برای اهداف و همچنین شاخص ها باید اوزان را نرمال نمود. جهت نرمال نمودن اوزان و محاسبه W هر وزن بر مجموع اوزان تقسیم می گردد.
W’ = [0.52, 0.85, 0.00, 1.00] مجموع اوزان = 0.52+0.85+0+1 = 2.37
W = [0.52/2.37, 0.85/2.37, 0.00/2.37, 1.00/2.37] = > W= [0.22, 0.36, 0, 0.42]
| W’ بردار وزنQ | 0.52 | 0.85 | 0.00 | 1.00 | |
| W نرمال Q | 0.22 | 0.36 | 0.00 | 0.42 | |
| W’ بردار وزن | 1.00 | 1.00 | W’ بردار وزن | 0.46 | 1.00 |
| W نرمال P1 | 0.50 | 0.50 | W نرمال P2 | 0.32 | 0.68 |
| W’ بردار وزن | 1.00 | 0.46 | W’ بردار وزن | 1.00 | 1.00 |
| W نرمال P3 | 0.68 | 0.32 | W نرمال P4 | 0.50 | 0.50 |
مرحله 4: محاسبه وزن نهایی گزینه ها
پس از ضرب هر یک از اوزان زیرمعیارها در وزن معیار اصلی وزن نهایی گزینه ها بدست می آید.
وزن نهایی دانشکده مهندسی =(0.22*0.68) +(0.36*0.5) +(0*0.5) +(1*0.32) =0.46
وزن نهایی دانشکده علوم پایه =(0.22*0.32) + (0.36*0.5) +(0*0.5) +(1*0.68) =0.54
درنهایت مشاهده می شود که دانشگاه علوم پایه با داشتن وزن بیشتر بهترین دانشکده دانشگاه است.
سوالات متداول در مورد روش AHP فازی (FAHP)
تفاوت روش «چانگ» (Extent Analysis) با روش «باکلی» (Geometric Mean) در چیست؟
روش چانگ به دلیل سادگی محاسباتی، محبوبترین متد در پایاننامههاست، اما یک نقد بزرگ به آن وارد است: در این روش گاهی وزن برخی معیارها به اشتباه «صفر» محاسبه میشود. در مقابل، روش باکلی که بر پایه میانگین هندسی فازی است، پیچیدگی بیشتری دارد اما نتایج آن بسیار دقیقتر و منطقیتر است و هرگز وزن معیار را صفر نمیکند. در آکادمی نرمافزار فرابگیر، ما معمولاً روش باکلی را برای مقالات علمی سطح بالا (ISI) پیشنهاد میدهیم تا از دقت ریاضی خروجیها اطمینان حاصل شود.
چگونه نرخ ناسازگاری را در محیط فازی محاسبه کنیم؟
محاسبه نرخ ناسازگاری در روش AHP فازی کمی متفاوت از روش قطعی است. روش رایج این است که ابتدا ماتریس فازی را به یک ماتریس قطعی (با استفاده از میانگین فازی) تبدیل کرده و سپس نرخ ناسازگاری را مشابه روش AHP قطعی به دست آوریم. اگر نرخ ناسازگاری کمتر از 0.1 باشد، یعنی قضاوتهای فازی خبره نیز دارای پایداری منطقی هستند. اگر این نرخ رعایت نشود، ابهام موجود در اعداد فازی نمیتواند بینظمی در قضاوتها را توجیه کند و پرسشنامه باید بازنگری شود.
آیا در روش AHP فازی هم به تعداد زیادی خبره نیاز داریم؟
خیر؛ یکی از مزایای روشهای فازی این است که به دلیل عمق اطلاعاتی هر عدد فازی، حتی با تعداد کمی خبره (مثلاً ۳ تا ۵ نفر) نیز میتوان به نتایج معتبری دست یافت. در واقع، کیفیت تخصص خبره در تصمیمگیری چندمعیاره (MCDM) بسیار مهمتر از تعداد آنهاست. اعداد فازی مثلثی به خوبی نوسانات کوچک در نظرات همین تعداد محدود را پوشش میدهند و با استفاده از میانگین هندسی فازی، خروجی نهایی به یک اجماع علمی و دقیق میرسد.
نتیجهگیری و جمعبندی نهایی
روش AHP فازی (FAHP) نقطه عطفی در گذار از تفکر سنتی به تفکر مدرن در مدیریت است. روش AHP فازی به ما میآموزد که برای رسیدن به دقتِ بیشتر، لزوماً نباید از اعداد صلب و قطعی استفاده کرد، بلکه باید «ابهام» موجود در واقعیت را به رسمیت شناخت. با مدلسازی ترجیحات انسانی به وسیله بازههای فازی، ما مدلی میسازیم که در برابر تغییرات جزئی در نظرات خبرگان، پایداری بیشتری نشان میدهد و خروجیهای آن در بخش آمار و تحلیل داده قابل اعتمادتر است.
در پیادهسازی این مدل، محقق باید توجه داشته باشد که هدف از فازیسازی، پیچیده کردن مسئله نیست، بلکه افزایش «روایی» نتایج است. انتخاب صحیح توابع عضویت و دقت در فرآیند دیفازیسازی، دو رکن اصلی هستند که موفقیت یک پروژه FAHP را تضمین میکنند. این متد به ویژه در کشورهای توسعهیافته برای تصمیمگیریهای حساس دولتی و صنعتی که با آیندهای غیرقطعی روبرو هستند، به شدت مورد استفاده قرار میگیرد.
ما در سایت فرابگیر بر این باوریم که تسلط بر ابزارهای فازی، مزیت رقابتی هر پژوهشگر در حوزه تحقیق در عملیات است. به همین منظور، استفاده از ابزارهای کمکی مانند فایل اکسل روش AHP فازی را توصیه میکنیم تا دغدغههای محاسباتی مانع از تمرکز شما بر تحلیلهای کیفی و مدیریتی نشود. با FAHP، شما نه تنها وزن معیارها را میسنجید، بلکه «اطمینان» را به فرآیند تصمیمگیری خود تزریق میکنید.