روش ANP فازی
روش تحلیل شبکه ای فازی (FANP) به طور گسترده ای برای محاسبه وزن های اولویت از ماتریس های مقایسه فازی استفاده شده است، زیرا نسبتا ساده تر از سایر روش ها مانند FAHP است. به عنوان مثال، گونری و همکاران(2009) از روش ANP فازی برای انتخاب مکان کارخانه کشتی سازی با استفاده از روش تجزیه و تحلیل توسعه یافته که توسط چانگ (1996) معرفی شده بود، استفاده کردند.
در نظر بگیرید X = {x1, x2, …, xn} یک مجموعه از اشیاء و U = {u1, u2, …,un} یک مجموعه از اهداف باشد. با توجه به روش تحلیل گسترده چانگ، هر شیء انتخاب شده و تحلیل وسعت هر هدف (gi) برای آن انجام می شود. بنابراین، m، مقادیر تحلیل وسعت هر شی را می توان با علائم زیر به دست آورد:
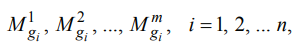
به طوری که در آن Mjgi(j=1,2,…,m) به موجب آن همه اعداد فازی مثلثی هستند. در اینجا مراحل روش تحلیل توسعه یافته چانگ ارائه شده است.
مرحله اول: مقدار وسعت مصنوعی فازی، با توجه به iمین شی، به صورت زیر تعریف می شود:
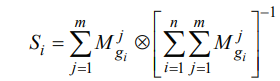
روش ANP فازی روش ANP فازی روش ANP فازی
برای به دست آوردن عملیات جمع فازی ( قسمت اول معادله S) مقادیر تحلیل وسعت m یک ماتریس خاص به صورت زیر انجام می شود:
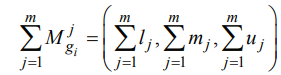
برای به دست آوردن، عملیات اضافی فازی ( قسمت دوم معادله S ) مقادیر به صورت زیر انجام می شود:
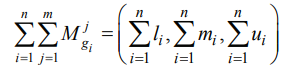
سپس، معکوس بردار در معادله بالا را به گونه ای محاسبه کنید که:
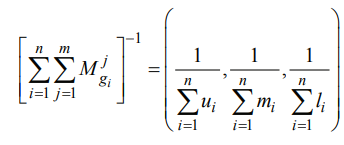
مرحله 2. درجه امکان M2 = (l2, m2, u2) ≥ M1 = (l1, m1, u1) به صورت زیر تعریف می شود:
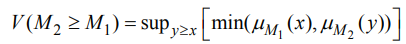
و می توان به طور معادل به صورت زیر بیان کرد:
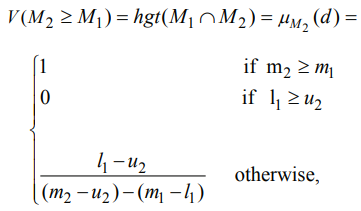
که در آن d منتخب بالاترین نقطه تقاطع D بین µm1 و µm2 است. برای مقایسه M1 و M2، به هر دو مقدار V(M1≥M2) و V(M2≥M1) نیاز داریم.
مرحله 3. درجه امکان بزرگتر بودن یک عدد فازی محدب از k اعداد فازی محدب
Mi (i = 1, 2, …, k) را می توان به صورت زیر تعریف کرد:
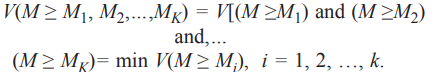
فرض کنید d’(Ai) = min V (Si ≥SK). برای k = 1، 2، …، n; k ≠ I. سپس بردار وزن به صورت زیر بدست می آید:
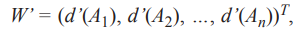
جایی که: Ai n عناصر هستند
مرحله 4. بردارهای وزن نرمال شده عبارتند از:
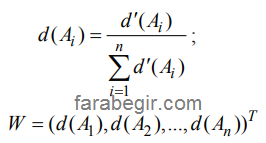
که در آن W یک عدد غیر فازی است.
