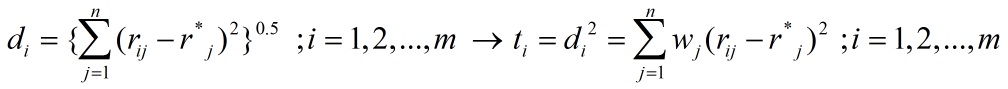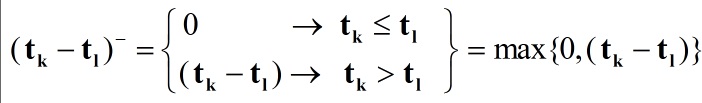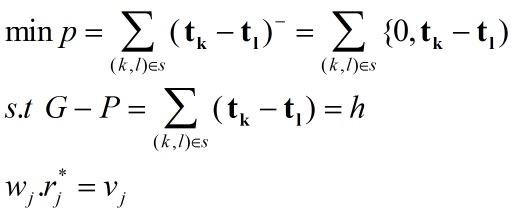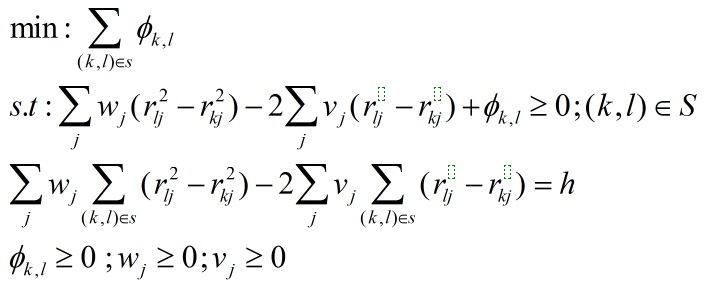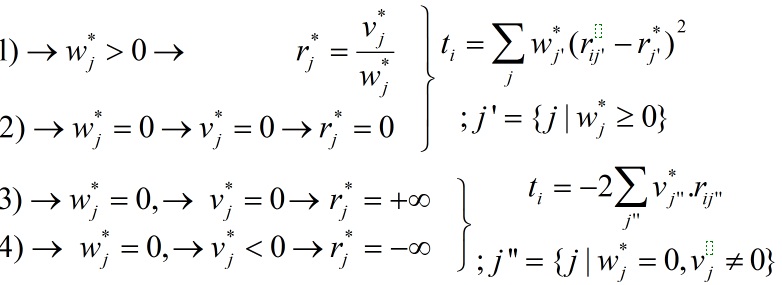روش LINMAP

در دنیای امروز که تصمیم‌گیری‌های چندمعیاره به‌طور روزافزون پیچیده می‌شوند، روش‌های تحلیلی پیشرفته‌ای برای ارزیابی گزینه‌ها مورد نیاز است. روش LINMAP (Linear Programming Multi‑Attribute Preference) یکی از این ابزارهای قدرتمند است که با ترکیب برنامه‌ریزی خطی و ارزیابی چندمعیاره، امکان انتخاب بهینه را فراهم می‌کند. این روش به‌ویژه در حوزه‌های مهندسی، مدیریت پروژه و اقتصاد کاربرد فراوانی دارد.

هدف این مقاله ارائه یک راهنمای کامل برای دانشجویان و پژوهشگرانی است که می‌خواهند با روش LINMAP آشنا شوند، آن را به‌صورت گام‌به‑گام اجرا کنند و مزایا و محدودیت‌های آن را درک کنند. در ادامه، با هشت زیرعنوان به تفصیل به بررسی این روش می‌پردازیم.

مفهوم و تاریخچه روش LINMAP

روش LINMAP در دههٔ ۱۹۷۰ توسط پژوهشگران حوزه تصمیم‌گیری چندمعیاره معرفی شد. این روش بر پایهٔ برنامه‌ریزی خطی (Linear Programming) ساخته شده و هدف آن ترکیب وزن‌های معیاری با مقادیر عملکردی برای یافتن گزینهٔ بهینه است.

در ابتدا، روش LINMAP برای حل مسائلی که شامل تعداد زیادی معیار و گزینه بودند، به‌کار گرفته شد؛ به‌طوری که معیارهای مختلف می‌توانستند به‌صورت نسبی وزن‌دار شوند. این ویژگی باعث شد تا این روش در مقایسه با روش‌های سنتی مانند AHP یا TOPSIS، انعطاف‌پذیری بیشتری داشته باشد.

تحقیقات بعدی بر روی بهبود الگوریتم‌های حل روش LINMAP متمرکز شد و به‌ویژه در زمینهٔ بهینه‌سازی ترکیبی (Mixed‑Integer Programming) گسترش یافت. امروزه، روش LINMAP به‌عنوان یک چارچوب تصمیم‌گیری چندمعیاره در مقالات علمی و پروژه‌های صنعتی به‌کار می‌رود.

از نظر نظری، روش LINMAP بر این اصل استوار است که هدف نهایی تصمیم‌گیرنده، کمینه‌سازی فاصلهٔ یک گزینه از نقطهٔ ایده‌آل (Ideal Point) در فضای معیارهاست. این مفهوم به‌صورت ریاضیاتی به‌کارگیری می‌شود تا بهترین ترکیب وزن‌ها و مقادیر عملکردی به‌دست آید.

مراحل اجرای روش LINMAP

اجرای روش LINMAP به‌صورت یک فرآیند گام‌به‑گام قابل پیگیری است. اولین گام، تعریف دقیق معیارها و جمع‌آوری داده‌های مربوط به هر گزینه است. در این مرحله، دقت در انتخاب معیارهای مرتبط و قابل‌سنجی بسیار مهم است؛ زیرا هر نقصی می‌تواند نتایج نهایی را تحت‌تأثیر قرار دهد.

پس از جمع‌آوری داده‌ها، گام دوم وزن‌دهی به معیارهاست. برای این کار می‌توان از روش‌های مختلفی مانند تحلیل سلسله‌مراتبی (AHP) یا روش‌های آماری استفاده کرد. وزن‌های به‌دست‌آمده سپس در معادلهٔ روش LINMAP جایگذاری می‌شوند.

فرض بر آن است که DM از دو گزینه مفروض نزدیکترین به ایده آل را انتخاب خواهد کرد و فاصله از ایده آل به صورت فاصله اقلیدسی وزین (di) برای گزینه Ai مورد توجه قرار می گیرد، همچنین اوزان Wj به منظور تبدیل مقیاس های موجود به مقیاس های یکسان بوده که ضمنا درجه اهمیت از هر شاخص را هم نشان می دهند.

فاصله گزینه Ai از ایدآل بدین صورت است:

به طوری که r^*_j نشان دهنده ایدآل از شاخص jام است.

الف) فرض کنیم مجموعه {(S={(k,l نشان دهنده زوج های A_k و A_l بوده به طوری که A_k  بر A_l ارحج است و مجموعه S به طور نرمال دارای m(m-1)/2 عنصر خواهد بود.

راه حل (*w,r) برای هر زوج مرتب شده سازگار با فاصله وزین است اگر t_k≤t_l  باشد.

مشخص نمودن راه حل (*w,r) باید چنان باشد که تجاوز از شرط  t_k<t_l در حداقل ممکن واقع شود.

ب)  اگر داشته باشیم t_k>t_l آنگاه مقدار  (t_k – t_l) بیانگر مقدار اشتباهی است که شرط مذکور در بند الف مورد تجاوز واقع می شود.

از این رو تعریف زیر را مدنظر قرار خواهیم داد:

بدین صورت ^–(t_l-t_k) نشان دهنده مقدار اشتباه برای زوج (k,l) می باشد و مجموع این اشتباهات عبارت است از:

p= درجه عدم تناسب = ∑_(k,l)∈S ( t_l – t_k ) ^–

مقدار p غیر منفی است لذا جهت مشخص نمودن راه حل (w,r) باید مقدار آن حداقل گردد.

ج) در مقابل P ارزش جدیدی به نام G درجه تناسب به صورت زیر تعریف می گردد.

G= درجه تناسب = ∑_(k,l)∈S ( t_l – t_k ) ⁺

د) راه حل (w,r)  از حل مساله زیر بدست می آید:

روش LINMAP

این مساله با استفاده از توابع هدف جدید Φ_k,l و الگوریتم می نی ماکس به صورت زیر تبدیل می شود:

ت) حالات استنتاج شده از این مدل

---

گام سوم شامل فرموله‌کردن مسئله به‌صورت برنامه‌ریزی خطی است. در این مرحله، تابع هدف به‌صورت کمینه‌سازی فاصلهٔ اقلیدسی بین گزینه‌ها و نقطهٔ ایده‌آل تعریف می‌شود و محدودیت‌های مربوط به وزن‌ها و مقادیر معیارها به‌عنوان قیود (Constraints) وارد می‌شوند.

در نهایت، با استفاده از نرم‌افزارهای حل‌کنندهٔ برنامه‌ریزی خطی (مانند LINGO، GAMS یا MATLAB) مسئله حل می‌شود و گزینهٔ بهینه بر اساس روش LINMAP شناسایی می‌گردد. نتایج به‌دست‌آمده می‌توانند به‌صورت جدول یا نمودارهای مقایسه‌ای ارائه شوند.

---

مثال روش LINMAP

ماتریس تصمیم زیر را در نظر بگیرید. مقایسات زوجی زیر از طرف تصمیم گیرنده مشخص شده است. به منظور دستیابی به مناسب ترین اوزان و راه حل ایده آل مساله را به روش LINMAP حل کنید.

مجموعه مقایسات زوجی:

S = {(1,2), (3,1), (4,1), (5,1), (2,3), (2,4), (2,5), (4,3), (3,5), (4,5)} | h=1 | landa = 0

X1	X2
A1	0	5
A2	5	4
A3	0	2
A4	1	3
A5	4	1

min { z12+ z31+ z41+ z51+ z23+z24+z25+z43+z35+z45}

w1	w2	-2v1	-2v2	min	v1	v2
(1,2)	25	-9	-10	2	+z(1,2)	5	-1
(3,1)	0	21	0	-6	+z(3,1)	0	3
(4,1)	-1	16	2	-4	+z(4,1)	-1	2
(5,1)	-16	24	8	-8	+z(5,1)	-4	4
(2,3)	-25	-12	10	4	+z(2,3)	-5	-2
(2,4)	-24	-7	8	2	+z(2,4)	-4	-1
(2,5)	-9	-15	2	6	+z(2,5)	-1	-3
(4,3)	-1	-5	2	2	+z(4,3)	-1	-1
(3,5)	16	-3	-8	2	+z(3,5)	4	-1
(4,5)	15	-8	-6	4	+z(4,5)	3	-2
sum	-20	2	8	4		=h	1

تابع هدف و ورودی نرم افزار WINQSB

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11	X12	X13	X14	dir	R.H.S
Min	1	1	1	1	1	1	1	1	1	1	0	0	0	0
C1	1	0	0	0	0	0	0	0	0	0	25	-9	-10	2	>=	0
C2	0	1	0	0	0	0	0	0	0	0	0	21	0	-6	>=	0
C3	0	0	1	0	0	0	0	0	0	0	-1	16	2	-4	>=	0
C4	0	0	0	1	0	0	0	0	0	0	-16	24	8	-8	>=	0
C5	0	0	0	0	1	0	0	0	0	0	-25	-12	10	4	>=	0
C6	0	0	0	0	0	1	0	0	0	0	-24	-7	8	2	>=	0
C7	0	0	0	0	0	0	1	0	0	0	-9	-15	2	6	>=	0
C8	0	0	0	0	0	0	0	1	0	0	-1	-5	2	2	>=	0
C9	0	0	0	0	0	0	0	0	1	0	16	-3	-8	2	>=	0
C10	0	0	0	0	0	0	0	0	0	1	15	-8	-6	4	>=	0
C11	0	0	0	0	0	0	0	0	0	0	-20	2	8	4	=	1

برای نرمال شدن ضربدر ضریب می کنیم تا عدد w*  و v* ساده شوند.

+z(1,2)	+z(3,1)	+z(4,1)	+z(5,1)	+z(2,3)	+z(2,4)	+z(2,5)	+z(4,3)	+z(3,5)	+z(4,5)	w*	v*	r*
0.25	0	0	0	0	0	0	0	0	0	0.0277	0.0554	0.0833	0.1944	3	3.5
1	2	3	7

محاسبه فاصله از نقطه ایده آل

r1j’	r2j’	r*1	r*2	w*1	w*2	ti
a1	0	5	3	3.5	1	2	13.5
a2	5	4	3	3.5	1	2	4.5
a3	0	2	3	3.5	1	2	13.5
a4	1	3	3	3.5	1	2	4.5
a5	4	1	3	3.5	1	2	13.5

لذا نقاط a2 و a4 کمترین فاصله را دارند و بهترین انتخاب ها می باشند.

---

کاربردهای روش LINMAP در صنایع مختلف

روش LINMAP به‌دلیل قابلیت ترکیب وزن‌های مختلف و ارزیابی چندمعیاره، در صنایع گوناگونی به‌کار گرفته می‌شود. در صنعت خودروسازی، برای انتخاب بهترین ترکیب قطعات با توجه به هزینه، وزن، دوام و ایمنی، روش LINMAP می‌تواند تصمیم‌گیری دقیق‌تری ارائه دهد.

در حوزه انرژی، این روش برای ارزیابی پروژه‌های تولید انرژی تجدیدپذیر (مانند خورشیدی و بادی) بر پایهٔ معیارهای اقتصادی، زیست‌محیطی و فنی استفاده می‌شود. با اعمال وزن‌های مناسب، روش LINMAP به تصمیم‌گیرندگان کمک می‌کند تا پروژه‌ای با بیشترین بازدهی کلی انتخاب کنند.

در مدیریت زنجیره تأمین، روش LINMAP برای انتخاب بهترین تأمین‌کننده بر اساس معیارهای هزینه، زمان تحویل، کیفیت و قابلیت اطمینان به‌کار می‌رود. این کاربرد باعث بهبود کارایی و کاهش ریسک‌های مرتبط با تأمین می‌شود.

همچنین در حوزه بهداشت و درمان، روش LINMAP می‌تواند برای ارزیابی روش‌های درمانی مختلف بر پایهٔ معیارهای هزینه، اثر بخشی، عوارض جانبی و رضایت بیمار استفاده شود؛ به‌طوری که تصمیم‌گیرندگان به‌صورت علمی‌ترین گزینه را انتخاب کنند.

مزایا و معایب روش LINMAP

یکی از مهم‌ترین مزایای روش LINMAP، توانایی ترکیب وزن‌های مختلف با مقادیر عملکردی به‌صورت ریاضیاتی دقیق است. این ویژگی باعث می‌شود تا تصمیم‌گیری‌ها شفاف‌تر و قابل توجیه‌تر باشند. همچنین، این روش نسبت به روش‌های رتبه‌بندی ساده، حساسیت کمتری به تغییرات جزئی در داده‌ها دارد.

از دیگر مزایا می‌توان به قابلیت استفاده از نرم‌افزارهای عمومی برنامه‌ریزی خطی اشاره کرد؛ به‌طوری که نیازی به ابزارهای خاص یا پیچیده نیست. این امر باعث می‌شود تا روش LINMAP برای دانشجویان و پژوهشگرانی که به‌دنبال راه‌حل‌های عملی هستند، مناسب باشد.

با این حال، روش LINMAP معایبی نیز دارد. یکی از مهم‌ترین آن‌ها نیاز به وزن‌دهی دقیق به معیارهاست؛ اگر وزن‌ها به‌درستی تعیین نشوند، نتایج ممکن است گمراه‌کننده باشند. همچنین، در مسائلی که تعداد معیارها بسیار زیاد باشد، مدل ممکن است به‌سرعت پیچیده شود و زمان حل آن افزایش یابد.

در نهایت، روش LINMAP برای مسائلی که معیارها به‌صورت غیرخطی یا وابستگی‌های پیچیده‌ای دارند، ممکن است مناسب نباشد؛ زیرا این روش بر پایهٔ برنامه‌ریزی خطی استوار است و فرض خطی بودن روابط را می‌پذیرد.

---

حساسیت تحلیل در روش LINMAP

تحلیل حساسیت (Sensitivity Analysis) در روش LINMAP نقش حیاتی در ارزیابی پایداری و استحکام نتایج ایفا می‌کند. این تحلیل به ما نشان می‌دهد که تغییرات کوچک در وزن‌های معیارها یا مقادیر عملکردی گزینه‌ها، چه تأثیری بر انتخاب نهایی خواهد داشت. اگر نتایج به‌شدت به تغییرات کوچک حساس باشند، نشان‌دهندهٔ عدم قطعیت در تصمیم‌گیری است و نیاز به بررسی بیشتر وجود دارد.

برای انجام تحلیل حساسیت در روش LINMAP، می‌توان وزن‌های معیارها را به‌صورت تدریجی تغییر داد و مشاهده کرد که آیا رتبه‌بندی گزینه‌ها تغییر می‌کند یا خیر. همچنین، می‌توان مقادیر عملکردی گزینه‌ها را در محدودهٔ معقولی تغییر داد و تأثیر آن بر نتیجهٔ نهایی را بررسی کرد. این تحلیل به تصمیم‌گیرندگان کمک می‌کند تا نقاط ضعف و قوت هر گزینه را بهتر درک کنند و ریسک‌های مرتبط با تصمیم‌گیری را کاهش دهند.

یکی از روش‌های رایج در تحلیل حساسیت، استفاده از نمودارهای عنکبوتی (Spider Charts) است. در این نمودارها، وزن‌های مختلف معیارها به‌صورت شعاعی نمایش داده می‌شوند و تغییرات وزن‌ها به‌صورت خطوط منحنی نشان داده می‌شوند. با بررسی این نمودارها، می‌توان به‌سرعت متوجه شد که کدام معیارها بیشترین تأثیر را بر انتخاب نهایی دارند.

تحلیل حساسیت در روش LINMAP به‌ویژه در مواردی که داده‌ها با عدم قطعیت همراه هستند، بسیار مهم است. برای مثال، اگر مقادیر عملکردی گزینه‌ها بر اساس تخمین‌های کارشناسان به‌دست آمده باشند، تحلیل حساسیت می‌تواند نشان دهد که چه میزان خطا در تخمین‌ها قابل قبول است تا رتبه‌بندی گزینه‌ها تغییر نکند.

مقایسه روش LINMAP با سایر روش‌های تصمیم‌گیری چندمعیاره

روش LINMAP تنها یکی از روش‌های موجود برای تصمیم‌گیری چندمعیاره است. روش‌های دیگری مانند AHP (Analytic Hierarchy Process)، TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) و آموزش جامع VIKOR (ViseKriterijumska Optimizacija i Kompromisno Resenje) نیز به‌طور گسترده‌ای مورد استفاده قرار می‌گیرند. هر یک از این روش‌ها دارای مزایا و معایب خاص خود هستند و برای مسائل مختلفی مناسب هستند.

AHP یک روش سلسله‌مراتبی است که بر مقایسهٔ زوجی معیارها و گزینه‌ها استوار است. این روش به‌ویژه برای مسائلی که ساختار سلسله‌مراتبی دارند، مناسب است؛ اما ممکن است در مواردی که تعداد معیارها زیاد باشد، زمان‌بر و پیچیده شود. روش LINMAP در مقابل، با استفاده از برنامه‌ریزی خطی، می‌تواند مسائل با تعداد معیار زیاد را به‌صورت کارآمدتری حل کند.

TOPSIS یک روش رتبه‌بندی است که گزینه‌ها را بر اساس فاصلهٔ آن‌ها از نقطهٔ ایده‌آل و نقطهٔ منفی ایده‌آل ارزیابی می‌کند. این روش ساده و قابل‌فهم است؛ اما ممکن است در مواردی که وزن‌های معیارها به‌درستی تعیین نشوند، نتایج دقیقی ارائه ندهد. روش LINMAP با ترکیب وزن‌های معیارها در معادلهٔ برنامه‌ریزی خطی، دقت بیشتری را فراهم می‌کند.

VIKOR یک روش بهینه‌سازی ترکیبی است که هدف آن یافتن گزینه‌ای است که کمترین مجموع فاصلهٔ از نقطهٔ ایده‌آل و بیشترین بهره‌وری را داشته باشد. این روش برای مسائلی که نیاز به مصالحه بین معیارهای مختلف وجود دارد، مناسب است؛ اما ممکن است در مواردی که معیارهای متضاد وجود داشته باشند، نتایج قابل قبولی ارائه ندهد. روش LINMAP با استفاده از برنامه‌ریزی خطی، می‌تواند به‌طور مؤثرتری با معیارهای متضاد مقابله کند.

چالش‌ها و راهکارهای بهبود روش LINMAP

با وجود مزایای فراوان، روش LINMAP با چالش‌هایی نیز مواجه است. یکی از مهم‌ترین چالش‌ها، نیاز به تعیین دقیق وزن‌های معیارهاست. اگر وزن‌ها به‌درستی تعیین نشوند، نتایج ممکن است گمراه‌کننده باشند. برای رفع این چالش، می‌توان از روش‌های وزن‌دهی ترکیبی استفاده کرد که نظرات کارشناسان و داده‌های آماری را با هم ترکیب می‌کنند.

چالش دیگر، پیچیدگی مدل در مسائلی با تعداد معیار زیاد است. برای کاهش پیچیدگی، می‌توان از روش‌های کاهش ابعاد (Dimensionality Reduction) استفاده کرد که تعداد معیارها را بدون از دست دادن اطلاعات مهم کاهش می‌دهند. همچنین، می‌توان از الگوریتم‌های بهینه‌سازی پیشرفته‌تر برای حل مدل استفاده کرد.

یکی از محدودیت‌های روش LINMAP، فرض خطی بودن روابط بین معیارها و گزینه‌هاست. در مواردی که روابط غیرخطی وجود داشته باشند، می‌توان از روش‌های برنامه‌ریزی غیرخطی (Nonlinear Programming) استفاده کرد. با این حال، این روش‌ها معمولاً پیچیده‌تر و زمان‌برتر هستند.

برای بهبود روش LINMAP، می‌توان از تکنیک‌های هوش مصنوعی (Artificial Intelligence) مانند شبکه‌های عصبی (Neural Networks) و الگوریتم‌های ژنتیک (Genetic Algorithms) استفاده کرد. این تکنیک‌ها می‌توانند به تعیین وزن‌های معیارها، کاهش پیچیدگی مدل و حل مسائل غیرخطی کمک کنند.

توسعه‌های اخیر در روش LINMAP

در سال‌های اخیر، پژوهشگران تلاش‌های زیادی برای توسعه و بهبود روش LINMAP انجام داده‌اند. یکی از مهم‌ترین توسعه‌ها، ترکیب این روش با روش‌های برنامه‌ریزی فازی (Fuzzy Programming) است. برنامه‌ریزی فازی به ما امکان می‌دهد تا عدم قطعیت در داده‌ها را به‌صورت ریاضیاتی مدل کنیم و تصمیم‌گیری‌های قوی‌تری ارائه دهیم.

توسعهٔ دیگر، استفاده از روش LINMAP در مسائل تصمیم‌گیری گروهی (Group Decision Making) است. در این مسائل، نظرات چندین تصمیم‌گیرنده باید با هم ترکیب شوند. روش LINMAP می‌تواند با استفاده از روش‌های تجمیع نظرات، به یک تصمیم‌گیری جمعی منسجم و قابل‌قبول کمک کند.

---

نتیجه‌گیری

روش LINMAP به عنوان یک ابزار قدرتمند در حوزه تصمیم‌گیری چندمعیاره، با ترکیب برنامه‌ریزی خطی و ارزیابی چندمعیاره، امکان انتخاب بهینه را در طیف گسترده‌ای از صنایع و کاربردها فراهم می‌کند. این روش با ارائه یک چارچوب ریاضیاتی دقیق، شفافیت و قابلیت توجیه نتایج را افزایش می‌دهد و به تصمیم‌گیرندگان کمک می‌کند تا با اطمینان بیشتری تصمیمات خود را اتخاذ کنند.

در این مقاله، به بررسی جامع روش LINMAP پرداختیم؛ از مفاهیم پایه و مراحل اجرا تا کاربردها، مزایا، معایب و چالش‌های آن. همچنین، به مقایسه این روش با سایر روش‌های تصمیم‌گیری چندمعیاره و توسعه‌های اخیر در این زمینه پرداختیم.

با وجود چالش‌هایی که روش LINMAP با آن مواجه است، همچنان یک ابزار ارزشمند برای تصمیم‌گیرندگان است. با استفاده از راهکارهای بهبود و توسعه‌های اخیر، می‌توان این روش را برای حل مسائل پیچیده‌تر و با عدم قطعیت بیشتر به‌کار برد.

در نهایت، روش LINMAP به عنوان یک ابزار مکمل برای تصمیم‌گیری انسانی عمل می‌کند و به تصمیم‌گیرندگان کمک می‌کند تا با در نظر گرفتن تمام جوانب و معیارهای مرتبط، بهترین گزینه را انتخاب کنند. با تسلط بر این روش، دانشجویان و پژوهشگران می‌توانند در حل مسائل واقعی و بهبود فرآیندهای تصمیم‌گیری نقش مؤثری ایفا کنند.

---

سوالات متداول (FAQ)