آموزش جامع روش SAW
در میان تمامی متدهای تصمیمگیری چندمعیاره (MCDM)، روش SAW به عنوان قدیمیترین و مستقیمترین روش شناخته میشود. فلسفه این متد بسیار ساده است: امتیاز نهایی هر گزینه، حاصلجمع ضرب امتیاز آن گزینه در وزن هر معیار است. به دلیل سادگی در درک و اجرا، این روش در اکثر پروژههای آموزش مدیریت به عنوان اولین گزینه برای رتبهبندی معرفی میگردد. اگر شما وزن معیارهای خود را از طریق وزندهی در AHP استخراج کرده باشید، روش SAW سریعترین راه برای رسیدن به رتبهبندی نهایی گزینههاست.
استفاده از این متد در دسته رتبهبندی گزینهها زمانی اولویت دارد که تصمیمگیرنده به دنبال شفافیت کامل در محاسبات است و پیچیدگیهای روشهایی مثل روش VIKOR را نمیپسندد. در روش SAW، فرض بر این است که معیارها با هم همپوشانی ندارند و اثر هر کدام به صورت خطی در نتیجه نهایی ظاهر میشود. اگرچه این روش ساده به نظر میرسد، اما دقت آن در گرو نرمافزارسازی صحیح دادهها و استفاده از وزنهای معتبر است که میتوان آنها را از روشهای عینی مانند روش انتروپی شانون نیز دریافت کرد.
بسیاری از محققان برای پروژههای بزرگ خود، به جای محاسبات دستی، از فایل اکسل روش SAW استفاده میکنند. این کار نه تنها سرعت انجام پروژه را در بخش تحقیق در عملیات بالا میبرد، بلکه امکان انجام تحلیل حساسیت را نیز فراهم میکند. در سایت فرابگیر، ما این روش را به عنوان زیربنای یادگیری روشهای پیشرفتهتری مثل روش TOPSIS میدانیم، زیرا درک منطق جبرانی (Compensatory) در این متد، کلید فهم سایر مدلهای تصمیمگیری است.
آنچه می خوانید
مفهوم روش SAW و جایگاه آن در تصمیمگیری
روش SAW یکی از ساده ترین و معمولی ترین روش های مربوط به MADM می باشد. این روش برای اولین بار در سال 1973 توسط مک کریمون ابداع شده است. در روش SAW تصمیم گیرنده به هر از معیارها یک وزن تخصیص می دهد که نشان دهنده اهمیت آن معیار می باشد.
روش SAW بدلیل سهولتی که دارد محبوب ترین و رایجترین روش در MADM است. روش SAW را میتوان سادهترین و مستقیمترین روش برای مواجهه با مسائل تصمیمگیری چندمعیاره در نظر گرفت؛ چرا که در این روش از یک تابع افزایشی خطی برای نمایش ترجیحات تصمیمگیرندگان استفاده میشود. با این حال این تکنیک زمانی کاربرد پیدا میکند که فرض کنیم ترجیحات مستقل و یا مجزا از هم هستند.
برای نشان دادن ارزیابی نهایی مطابق معیارها، تصمیم گیرنده یک مقیاس عددی (کمی) از ارزش داخلی معیارها را ایجاد می کند. تصمیم گیرنده سپس می تواند به سادگی با ضریب نرخ مقیاس برای هر ارزش معیار با اهمیت وزن نشان دهنده معیار و جمع آن ها یک مقیاس نهایی برای هر آلترناتیو را ایجاد می کند.
روش SAW که مخفف Simple Additive Weighting است، امتیاز کلی یک راه حل کاندید با مجموع وزنی تمام مقادیر ویژگی تعیین می شود. روش ساده وزنی به دلیل سهولتی که دارد محبوب ترین و رایج ترین روش در MADM است.
روش SAW را می توان ساده ترین و مستقیم ترین روش مواجهه با مسائل تصمیم گیری چند معیاره در نظر گرفت. در این روش از یک تابع افزایش خطی برای نمایش ترجیحات تصمیم گیرندگان استفاده می شود . با این حال این تکنیک زمانی کاربرد دارد که فرض شود ترجیحات مستقل یا مجزا از هم هستند.
در این روش جهت تصمیم گیری، تنها به ماتریس تصمیم گیری و بردار وزن شاخص های ارزیابی نیاز است. این روش مانند روش ویکور و تاپسیس عمل می کند اما به روشی بسیار ساده تر. در این روش که با نام روش ترکیب خطی وزن دار نیز شناخته می شود، پس از بی مقیاس کردن ماتریس تصمیم، با استفاده از ضرایب وزنی معیارها، ماتریس تصمیم بی مقیاس وزن دار به دست آمده و با توجه به این ماتریس، امتیاز هر گزینه محاسبه می شود.
بعد از اینکه وزن نهایی هر آلترناتیو تخمین زده می شود، آلترناتیو با بالاترین وزن ( بالاترین متوسط وزن) برای تصمیم گیرنده ایجاد می شود.
گام های روش SAW
گام اول: تشکیل ماتریس تصمیم
ماتریس تصمیم این روش شامل جدول است که ستونهای آن را معیارها یا زیرمعیارها و سطرهای آن را گزینهها تشکیل میدهند.

گام دوم: بی مقیاس کردن ماتریس تصمیم
برای بی مقیاس کردن ماتریس تصمیم در روش Saw به طریق زیر عمل میکنیم.
- اگر معیار مثبت باشد: تک تک اعداد آن ستون را بر بزرگترین عدد تقسیم میکنیم.
- اگر معیار منفی باشد: مینیمم آن ستون تقسیم بر تک تک اعداد میشود.
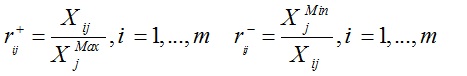
گام سوم: تشکیل ماتریس موزون
در این گام براساس وزن معیارها، ماتریس موزون را بدست میآوریم. . در این گام با توجه به وزن های محاسبه شده از روشهای دیگر (AHP، آنتروپی شانون، CRITIC و دیگر روش ها)، ماتریس وزن دار را بدست می آوریم.

گام چهارم: انتخاب گزینه برتر
با جمع سطری ماتریس وزنها امتیاز هر گزینه محاسبه میشود و بر اساس آن گزینهها رتبه بندی میشوند. سپس آلترناتیو ارحج A* به صورت زیر انتخاب می شود ( کین و همکاران 2008).
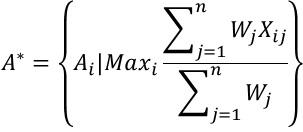
که Xij خروجی آلترناتیو iام و صفت jام با یک مقیاس کمی قابل مقایسه است. اغلب وزن ها نرمالایز شده هستند یعنی
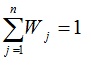
روش وزندهی ساده یکی از نخستین و سادهترین روشهای تصمیمگیری چندشاخصه است. در این روش از یک ماتریس تصمیم برای ارزیابی تعدادی گزینه براساس تعدادی معیار استفاده میشود. اگرچه روش حل مساله با میانگین موزون تفاوت چندانی ندارد اما گامهای انجام این روش مقدمه خوبی برای فراگیری سایر روشهای تصمیمگیری چندشاخصه است.
با وجود سادگی، رعایت دقت در تمامی مراحل الزامی است. کوچکترین خطا در نرمافزارسازی، کل رتبهبندی را با چالش مواجه میکند. به همین دلیل است که محققان حرفهای ترجیح میدهند از ابزارهای آماده استفاده کنند تا از صحت روابط ریاضی اطمینان یابند. این روش به ویژه در مطالعاتی که تعداد گزینهها زیاد است، کارایی فوقالعادهای دارد و به سرعت نمایی از وضعیت رقابتی میان شاخصها را ترسیم میکند.
مثال عددی روش SAW
فرض کنید فردی می خواهد از بین سه نوع سیستم کامپیوتری ، با روش SAW یک نوع را انتخاب کند. هر نوع سیستم ، با پنج شاخص که عبارتند از هزینه، عمر مفید، کیفیت، خدمات پس از فروش، کیفیت سخت افزار و کیفیت نرم افزار ارزیابی می شود. ماتریس تصمیم گیری این مساله ، به صورت جدول زیر می باشد. گزینه ها با Ai و شاخص ها با Cj نشان داده شده اند.
| معیار / گزینه | C1 | C2 | C3 | C4 | C5 |
| A1 | 30 | 20 | متوسط | خیلی زیاد | کم |
| A2 | 10 | 30 | زیاد | متوسط | زیاد |
| A3 | 20 | 50 | خیلی زیاد | کم | خیلی زیاد |
گام اول: تبدیل شاخص کیفی به شاخص کمی. برای این کار می توان از مقیاس فاصله ی دو قطبی ( ساعتی) استفاده کرد.
| معیار / گزینه | C1 | C2 | C3 | C4 | C5 |
| A1 | 30 | 20 | متوسط | خیلی زیاد | کم |
| A2 | 10 | 30 | زیاد | متوسط | زیاد |
| A3 | 20 | 50 | خیلی زیاد | کم | خیلی زیاد |
از جدول متغیرهای کلامی معادل عددی آن را برای استفاده در ماتریس تصمیم نهایی استخراج می کنیم.
| اصطلاح زبانی فارسی | اصطلاح زبانی لاتین | عدد متناظر |
| ترجیح کامل | Extremely preferred | 9 |
| ترجیح خیلی قوی | Very strongly preferred | 7 |
| ترجیح قوی | Strongly preferred | 5 |
| ترجیح کم | Moderately preferred | 3 |
| ترجیح یکسان | Equality preferred | 1 |
| ترجیحات بین فواصل | 2,4,6,8 |
سپس معادل عددی کلیه معیارها را برای تشکیل ماتریس نهایی جایگزین می نماییم.
| معیار / گزینه | C1 | C2 | C3 | C4 | C5 |
| A1 | 30 | 20 | 5 | 9 | 3 |
| A2 | 10 | 30 | 7 | 5 | 7 |
| A3 | 20 | 50 | 9 | 3 | 9 |
گام دوم: اکنون باید این ماتریس تصمیم کمی، بی مقیاس شود. نوع بی مقیاس سازی این روش تصمیم گیری چندشاخصه «بی مقیاس سازی خطی » می باشد ( توجه : شاخص اول منفی است. )
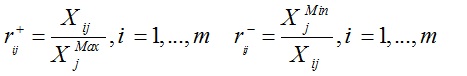
| معیار / گزینه | C1- | C2+ | C3+ | C4+ | C5+ |
| A1 | 30 | 20 | 5 | 9 | 3 |
| A2 | 10 | 30 | 7 | 5 | 7 |
| A3 | 20 | 50 | 9 | 3 | 9 |
| MAX | 30 | 50 | 9 | 9 | 9 |
| MIN | 10 | 20 | 5 | 5 | 3 |
سپس اوزان نهایی را بر اساس مقادیر حداکثر و حداقل محاسبه می کنیم.
| معیار / گزینه | C1 | C2 | C3 | C4 | C5 |
| A1 | 0.333 | 0.4 | 0.556 | 1 | 0.333 |
| A2 | 1 | 0.6 | 0.778 | 0.556 | 0.778 |
| A3 | 0.5 | 1 | 1 | 0.333 | 1 |
(شاخص منفی) A11 = 10 /30 = 0.333
(شاخص مثبت) A21 = 20/50 = 0.4
مزایا، محدودیتها و مقایسه با سایر روشها
بزرگترین مزیت روش SAW، بصری بودن و سادگی تفسیر آن برای مدیران است. برخلاف روشهای پیچیده برتری مانند روش PROMETHEE، در اینجا به راحتی میتوان توضیح داد که چرا یک گزینه رتبه اول را کسب کرده است. اما این سادگی یک محدودیت نیز دارد: این روش تضادهای شدید بین معیارها را به خوبی روشهایی مثل ویکور مدیریت نمیکند. همچنین، در روش SAW فرض میشود که تصمیمگیرنده نسبت به تغییرات معیارها ریسکneutral است.
در مقایسه با روش TOPSIS، روش SAW به دادههای خام نزدیکتر است چون از توان دوم و ریشه در نرمالسازی استفاده نمیکند. بسیاری از داوران در بخش وزندهی معیارها و رتبهبندی، از دانشجو میخواهند که نتایج SAW را به عنوان یک معیار پایه (Baseline) در کنار روشهای نوین ارائه دهد. این کار باعث میشود اعتبار تحلیلهای شما در ژورنالهای علمی دوچندان شود.
در نهایت، اگر به دنبال رتبهبندی سریع در محیط اکسل هستید و پیچیدگیهای آماری مد نظر شما نیست، روش SAW بهترین انتخاب است. این روش در رشتههای مهندسی، محیطزیست و آموزش مدیریت کاربرد وسیعی دارد. برای کسانی که میخواهند از دقت ترکیبی بهرهمند شوند، مطالعه روش WASPAS که ترکیبی از SAW و مدل ضربی است، پیشنهاد میگردد تا پایداری نتایج خود را به سطح بالاتری برسانند.
سوالات متداول در مورد روش SAW
آیا مجموع وزنها در روش SAW حتماً باید برابر با یک باشد؟
بله؛ برای اینکه نتایج نهایی قابل مقایسه و استاندارد باشند، وزنهای ورودی (از هر روشی که استخراج شدهاند) حتماً باید نرمال شده و مجموع آنها برابر ۱ باشد.
تفاوت اصلی SAW با روش مجموع وزنی ضربی (WPM) چیست؟
در SAW امتیازها با هم جمع میشوند، اما در WPM امتیازها در هم ضرب شده و به توان وزن میرسند. ترکیب این دو روش منجر به ایجاد متد قدرتمند واسپاس میشود.
چرا در روش SAW از نرمالسازی خطی استفاده میکنیم؟
چون این نوع نرمالسازی فاصله نسبی بین گزینهها را به بهترین شکل حفظ کرده و فهم ریاضی آن برای غیرمتخصصان آسانتر است.
نتیجهگیری
روش SAW به دلیل سادگی در اجرا و شفافیت در منطق ریاضی، همچنان محبوبترین ابزار در میان محققان برای رتبهبندی گزینهها است. این روش به شما اجازه میدهد تا با کمترین پیچیدگی، وزنهای به دست آمده از بخش وزندهی معیارها را مستقیماً در تصمیمگیری خود دخالت دهید. اگرچه روشهای مدرنتری نیز ابداع شدهاند، اما یادگیری SAW پایه و اساس درک تمامی متدهای حوزه تصمیمگیری چندمعیاره (MCDM) است و استفاده از آن در کنار سایر روشها، اعتبار تحلیلهای شما را تضمین میکند.
